Трассировка проводного монтажа (ТПМ) (провода с изоляцией)

ТПМ. осуществляться по прямым, соединяющим выводы эл-ты (монтаж в навал) или с помощью жгутов, к-е прокладывается в специальных каналах. Ограничения: количество проводников, к-е можно подсоединить к 1 выводу и число проводов в каждом жгуте – пропускная способность каналов.

ТПМ заключается в определении порядка соединения выводов в соответствии со схемой или с учетом ограничений. Критерий качества – минимальной суммарной длиной проводников. Нахождение порядка соединения выводов модулей внутри цепи сводится к задаче нахождения КСД.

Будем использовать модель схемы(цепи) в виде графа, в к-м выводов элементов сопоставлены вершины и на этой вершине строится полный граф цепи. Число вершин графа = n, при этом число ребер полного графа r=n(n-1)\2

При таком подходе каждая цепь представляется отдельной компонентой связности.

Ставится задача построения КСД на тех комп-х связности число вершин которых>2.

Отметим, что на n вершинах полного графа можно построить tn деревьев

Точные решения задачи построения КСД методом полного перебора нецелесообразны. Существуют приближенные алгоритмы решения этой задачи, дающие результаты достаточно близкие к оптимальным.

Алгоритм Красккала

Пусть задан G=(X,V) i,j=1,n, i≠j

Каждому ребру Vij поставлено в соответствие число Cij – вес или длина данного ребра.

Ставится задача: среди всех деревьев (n-(n-2)), кот. м. выделить в данном графе, требуется найти дерево с минимальной длиной в дереве (n-1) ребро.

Пусть C=[c_ij]_n*n матрица длины ребер графа.

1. Все ребра графа n(n-1)\2 упорядочива-ся п порядке убывания длины, начиная с ребра C1=min_i,jCij

……

Cn=max_i,jCij

2. Последовательно просматривается рассматриваемое множество V* длин ребер на каждом шаге, включенным в дерево одно ребро. В качестве такого ребра выбирается ребро среди не включенных в дерево, имеющих минимальную длину и не образующих циклов с ребрами уже вошедших в дерево.

3. Отметим: при работе этого алгоритма возможно появление несвязных поддеревьев, которое затем соединяется, образуя одну компоненту связности.

Недостатки:

1) Необходимо на каждом шаге проверять условия необраз-я цикла, а так же наблюд-е за различными компонентами связности.

2) Большое время уходит на упорядочивание ребер полного графа.

Алгоритм Прима.

Использует тот же принцип соединения ближайших вершин, что и алг. Краскала, но на каждом шаге к строящемосю дереву присоед-ся ближайшая изолированная вершина.

В основе лежат 2 теоремы:

T.1. Каждая вершина КСД непосредственно связана по крайней мере с 1 ближайшей вершиной.

Т.2. Каждый измеряемый фрагмент поддерева связан по крайней мере с 1 из излир-х фрагментов кратчайшим ребром.

В соответствии с Т.1. построение КСД м.б. начато с произвольной вершины графа:

1) Выбираем, например, x1 и находим кратчайшее ребро, инертное этой. Это б. ребро .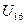

2) Включаем в КСД, вычеркиваем 1 и 6 столбцы (чтобы не было циклов), помечаем 6 строку и выбираем из нее минимальный элемент .

3) Включаем в КСД 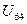, вычеркиваем 4 столбец, помечаем 4 строку и выбираем из нее минимальный элемент =1.

4) Включаем в КСД , помечаем строку 5, вычеркиваем 5 столбец, выбираем 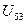=5.

5) Включаем в КСД, вычеркиваем 3 столбец, помечаем 3 строку и выбираем из неё =1.

КСД построено.

 

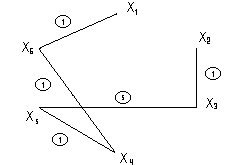Т.о. на Т шаге алг-ма исп. Т1, и далее Т2.

Здесь всегда Т компонента связности, т.е. Т разрастается по дереву.

 

Алгоритм Прима построения КСД при огран-х на лок-е степени вершины.

Лок. степени b - число ребер графа, инцидентных этой b. Т.к. задача возникает при проектировании проводных соединений, когда ограничено число паек к 1 контакту. Чаще всего кол. паек к контакту = 2.

предположим, что зад. матрица U длины ребер графа цепи и необходимо построить КСД при .

Для решения дан. задачи м. применить алг. Прима с вычеркиванием строки, соответ-ей вершине лок. степени кот. стан. =n.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: