 |
Математическая постановка задачи компоновки с использованием модели ВНГ
|
|
|
|
Критерий оптимизации – число межблочных связей. ВНГ будем представлять в виде матрицы C.
Введем в рассмотрение матрицу решений ξ, которая определяет вариант компоновки элементов схемы в блоки.
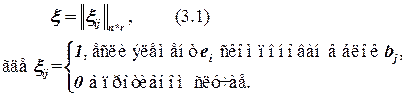
На элементы матрицы решений накладываются следующие ограничения:
Т.е. каждый элемент может быть расположен только в одном блоке.
Число элементов в блоке должно быть не больше заданного.
Выведем формулу для числа внешних выводов блока.
Очевидно, что выражение 
означает число межблочных связей, которые выходят из блока bj от элемента ei на элемент ek,расположенный вне блока bj.
Очевидно, что выражение 
означает число межблочных связей, выходящих из блока bj от элемента ei на все остальные элементы схемы, расположенные вне блока bj, включая элемент e0.
Для того, чтобы получить общее число выводов от блока bj, необходимо просуммировать предыдущее выражение по i:
Теперь получим формулу для суммарного числа межблочных связей:
С учетом выражения (3.2) второй член выражения (3.5) перепишем в виде:
– число связей с внешним разъемом схемы.
Поэтому в качестве можно взять первую часть целевой функции (3.5). Т.о., необходимо найти такую матрицу решений ξ, удовлетворяющую ограничениям (3.2)–(3.4), для которой обеспечивается минимум целевой функции (3.5). Данная задача является задачей квадратичного целочисленного программирования с булевыми переменными cij.
В связи с тем, что модель ВНГ является грубой моделью, то и полученные формулы (3.4), (3.5) носят грубый характер.
Для примера рассмотрим схему, приведенную на рисунке 3.1.
Рис. 3.1
ВНГ для данной схемы приведен на рисунке 3.2 (примечание: вес ребра на рисунке обозначен количеством связей).
|
|
|
Пусть требуется разбить приведенную схему на блоки с ограничениями:
.
Из рассмотрения ВНГ нетрудно видеть, что по данной модели невозможно разбить схему не только на два, но и на четыре блока. На самом же деле это не так (см. схему). Это говорит о неточности данной модели.
ВОЛНОВОЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
ТРАССИРОВКИ.
Большинство алгоритмов конфигурации печатных проводников используют идею волнового алгоритма Ли, который представляет собой процедуру нахождения кратчайшего пути в графе.
В работе Ли плоскость монтажа разбивается на элементарные прямоугольники (ячейки), со стороной равной расстоянию между осями соседних печатных проводников. Минимальная величина прямоугольника (ячейки) определяется технологическим оборудованием.
При использовании ДРП, включение элементарной ячейки в путь означает проведение печатного проводника, так как показано на рисунке 1.
 |
Рис. 1.
Считаем, что основная координатная сетка смещена на h/2, чтобы пути следовали из ячейки в ячейку, а не по координатным линиям ДРП.
На каждом шаге алгоритма некоторые ячейки ДРП – заняты. Ячейки, попадающие в область запрещённых для трассировки: краевые поля платы, зоны размещения элементов и их выводы, ранее проведённые проводники.
Основа алгоритма Ли – процедура поиска оптимального, в смысле некоторого критерия, пути между двумя ячейками, при соблюдении ряда условий:
| А | ||||
| ´ | ||||
| В |
· Первая часть алгоритма моделирует процесс распространения волны от элементарной площадки А по свободным ячейкам ДРП. При распространение волны от А, алгоритм последовательно строит Ф1(А), Ф2(А), …, Фk(А) её фронты. Множество ячеек входящих в i-е фронты для всех i≤k – это окрестность ячейки А. Оk(А).
Если проведение пути возможно, то на k+1 шаге окажется, что ВÎОk+1(А), если в следующий фронт не удаётся включить ни одной свободной ячейки, т.е.
|
|
|
Оk(А)= Оk+1(А), то при данных условиях путь провести невозможно.
Т.о. первая часть алгоритма Ли определяет возможность проведения пути между А и В.
· Во второй части алгоритма Ли, начиная с В по определённым правилам выполняем переход от ячейки k -го фронта к ячейки k -1 фронта, до тех пор, пока не будет достигнута А. Пройденные ячейки – искомый путь.
Условия, которые д. б. выполнены при проведении пути и возможность оценки его оптимальности д.б. заложены в правила, по которым происходит движение фронта.
Для ячеек ДРП устанавливается отношения соседства (общее ребро). Распространение волны заключается в присваивании соседним ячейкам значения весовой функции. Вес ячейки k -го фронта Pk является функцией веса ячейки k-1 фронта. В общем случае к весам ячеек предъявляются следующие требования: Pk-1¹ Pk ¹ Pk+1, в большинстве модификаций алгоритма Ли на веса ячеек накладывается ограничение: Pk> Pk-1. В этом случае проведение пути заключается в переходе от А к В, т.о. чтобы Pk монотонно убывало. При этом возможен вариант, когда несколько ячеек соседних с данной имеют одинаковый вес. Для однозначного выбора при учёте критерия минимального кол-ва изгибов проводника следует сохранить направление движения. Если приходится делать поворот, то учитываем заранее заданный порядок предпочтений.
Т.к. алгоритм Ли представляет собой алгоритм нахождения кратчайшего пути в графе, то он легко распространяется на многослойный печатный монтаж, при использовании модификации в виде графа. При наличии ограничения на переходы со слоя в слой можно увеличить вес ребра, соединяющего две смежные вершины графа на соседних слоях, по сравнению с весом ребра графа соединяющего вершины в одном слое. В общем случае весовая функция может зависить от параметров учитывающих длину пути, числа переходов из слоя в слой, степень близости пути к другому и т.д. Например, в виде аддитивной функции:
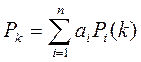
аi – весовой коэффициент, учитывающий важность i-го параметра.
Pi(k) – значение учитываемого параметра.
Усложнение функции веса увеличивает объём информации на одну ячейку ДРП и время работы 1-й части алгоритма. При практической реализации алгоритма Ли важная проблема – сокращение объёма памяти необходимого для запоминания весов ячеек. При вычислении весов ячеек по выражению: Pk=Pk-1+1 ячейка м.б. в следующих состояниях: свободна, занята или имеет вес от 1 до L (максимально возможная длина пути, определяемое как кол-во ячеек ДРП в пути).
|
|
|
Необходимое, для запоминания состояния одной ячейки, число 2-х разрядов памяти:
«Замечание: перед логарифмом стоит символ = зеркальное отражение Г»
Наиболее эффективным способом кодирования состояния ячеек ДРП является: метод путевых координат по модулю 3. При выборе последовательности, ячеек на этапе построения пути по методу путевых координат, для каждой ячейки, начиная с В (в случае соседства по рёбрам), достаточно знать от какой соседней ячейки в неё пришла волна: ¯(3), ®(2), (1), (4). Т.о. ячейка здесь может иметь следующие признаки: свободна, занята, одна из путевых координат, следовательно, число разрядов для кодирования состояния ячеек равно 3.
Путевой координатой Ci фронта Фk является та соседняя с ней ячейка Cj фронта Фk-1, от которой Ci получила свой вес.
При использовании метода путевых координат соседним ячейкам присваиваются веса в соответствии с пожеланиями пользователя. При проведении пути следует двигаться направлении противоположном распространению волны, в соответствии с путевыми координатами.
|
|
|
