Генетический алгоритм трассировки двухслойных каналов. Горизонтальные и вертикальные ограничения.

Канальные алгоритмы базируются на представлении о каналах и магистралях. Магистралью называют отрезок прямой, по которому может проходить соединение в преимущественном направлении.

Канал – это область прямоугольной формы, на одной или нескольких сторонах которой расположены контакты с системой однонаправленных магистралей.

Каждая цепь, т.е. соединение эквипотенциальных контактов, представлена как одиночный горизонтальный сегмент с несколькими вертикальными сегментами, которые соединяют горизонтальный сегмент с контактами цепи.

Горизонтальные сегменты располагаются в одном слое, вертикальные – в другом. Соединения между горизонтальными и вертикальными сегментами делаются через переходные отверстия.

Основная задача канальной трассировки – выбор наименьшей ширины канала, достаточной для размещения в нём всех соединений и назначения соединений на магистрали. Кроме того, необходимо минимизировать суммарную длину соединений (цепей), число переходных отверстий и т. д.

Задача канальной трассировки в классической постановке основана на трассировке двухстороннего канала, по верхней и нижней сторонам которого проходят линейки контактов.

Изломы, т. е. переходы горизонтального участка с одной магистрали на другую, не допускаются.

Рисунок 1.

Канал описывается двумя последовательностями top и bottom, в которых размещаются верхняя и нижняя линейки контактных площадок (○) канала соответственно. Размер обеих последовательностей равен числу колонок в канале. Множество цепей распределяется как Net = {N1, N2, …, Nn}, где «n» – число цепей.

Горизонтальные и вертикальные ограничения.

При канальной трассировке не допускаются наложения вертикальных и горизонтальных сегментов цепей. Для решения этой задачи вводятся графы вертикальных и горизонтальных ограничений.

Вертикальные ограничения описываются ориентированным графом вертикальных ограничений GV = (ENet, EV), где ENet – множество вершин, соответствующих множеству цепей Net; EV – множество направленных ребер. Ребро (n, m) Є EV существует тогда и только тогда, когда цепь n должна быть расположена выше цепи m для предотвращения наложений вертикальных сегментов цепей.

Например, на рис.2 в графе GV существует путь из вершины 1 в вершину 6. Это означает, что цепь 1 должна быть расположена выше цепи 6, для того, чтобы не было наложений вертикальных сегментов на первых и шестых контактах. Чтобы задача решалась в рамках классической постановки, граф GV должен быть ациклическим, иначе задача может быть решена только с введением изломов, а это и противоречит условиям классической постановке задачи канальной трассировки.

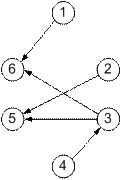
Рисунок 2.

Далее будет использоваться расширенный граф вертикальных ограничений

GRV = (ENet, ERV), где ENet – множество вершин, соответствующих множеству цепей Net; ERV – множество направленных ребер. Ребро (n, m) Є ERV существует тогда и только тогда, когда в графе GV существует путь из вершины n в вершину m. Например, на рис. 2 в GV есть путь из вершины 4 в вершину 5 через вершину 3. Следовательно, в GRV существует ребро (4, 5), а также ребро (4, 6). Для нашего примера GRV приведён на рис.3.

Рисунок 3.

Горизонтальные ограничения представлены неориентированным графом горизонтальных ограничений GН = (ENet, EH), где ENet – множество цепей; EH – множество рёбер. Ребро (n, m) Є EН существует тогда и только тогда, когда магистрали для цепей n и m должны быть разными для исключения наложения горизонтальных сегментов цепей.

Например, в GН (рис. 4.) ребро (1,4) означает, что цепь 1 не может размещаться на одной магистрали с цепью 4.

Рисунок 4.