Алгоритм парных перестановок конструктивных модулей.

Суть этого итерационного алгоритма заключается в последовательном целенаправленном улучшении произвольного начального размещения модулей на плате по выбранному критерию путем парных перестановок. С этой целью на каждой итерации алгоритма осуществляет вычисление приращений суммарной длины всех связей для всевозможных парных перестановок модулей. Из всего множества перестановок, дающих отрицательные приращения, выбирается подмножество, которое удовлетворяет следующим требованиям:

· выбранное подмножество перестановок позволяет максимально уменьшить суммарную длину всех связей;

· подмножество образует лишь независимые перестановки, т. е. такие парные перестановки, в которые входят модули, несвязанные с модулями других переставляющихся пар.

Далее осуществляются перестановки выделенных таким образом пар модулей и переход к следующей итерации.

Описанный итерационный процесс сходится к локально-оптимальному размещению модулей на плате. Выведем формулы для суммарной длины L всех связей и ее приращения ∆L при перемещении модулей.

Пусть имеется плоская или объемная плата с узлами, предназначенными для установки модулей. Задана матрица расстояний между отдельными узлами платы, где , либо , где , и , – координаты i-го и j-го узлов платы.

Даны некоторые совокупности m модулей подлежащих размещению (m≤n) и матрица числа связей этих модулей между собой. t1

Пусть на некоторой итерации имеется следующее размещение модулей на плате:

где tl– номер модуля, оказавшегося размещенным в l-м узле платы.

Поставим в соответствие этому варианту размещения матрицу связей . Элемент матрицы R равен числу связей между модулями tiи tj, находящимися на данной итерации в узлах i и j соответственно.

Поскольку расстояние между узлами i и k равно dik, то суммарная длина связей между модулями tiи tkравна: 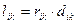(1).

Отсюда суммарная длина связей ti-го модуля, расположенного в i-ом узле платы, со всеми остальными модулями схемы равна: (2).

Для суммарной длины всех связей при данном варианте размещения получаем формулу:

(3).

Найдем теперь формулу для приращения суммарной длины всех связей при перестановке модулей tiи tjрасположенных в узлах i и j соответственно.

Для суммарной длины связей ti-го и tj-го моделей со всеми остальными модулями схемы имеем: (4), где последнее слагаемое соответствует удвоенной длине связей между модулями, расположенными в i-ой и j-ой позициях.

При взаимной перестановке модулей с номерами tiи tj, суммарная длина их связей со всеми остальными модулями определяется из выражения: (5).

Заметим, что взаимная перестановка модулей с номерами tiи tjсоответствует перестановке строк и столбцов в матрице R.

Вычитая из выражения (5) выражение (4), определим приращение суммарной длины всех связей после перестановки модулей с номерами tiи tj:

(6).

Введем в рассмотрение матрицу P=RxD, элементы которой (7).

Нетрудно видеть, что полусумма диагональных элементов матрицы P (полуслед) равна суммарной длине всех связей, определяемой формулой (3).

С помощью элементов матрицы P могут быть легко вычислены элементы ∆Lijматрицы приращений для всех парных перестановок.

С учетом симметричности матрицы D, выражение (6) преобразуется к виду: 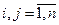(8), где (9)

Вычисляя по формулам (8) и (9) элементы матрицы приращений можно выбрать подмножество перестановок, удовлетворяющих перечисленным выше требованиям.