И многозабойным скважинам в однородном пласте

ограниченной толщины [27, 36, 5, 16]

Выше рассмотрены задачи о при­токе жидкости к многозабойным скважинам в слоистом пласте. При этом основное гидродинамическое предположение со­стояло в том, что фильтрация пластовой жидкости в каждом отдель­ном горизонтальном слое определена как плоское течение.

Тем не менее, фильтрацию к горизонтальным или наклонным скважинам, дренирующим горизонтальный пласт ограниченной толщины, необходимо рассматривать с учетом вертикальной составляю­щей потока. Ниже изложим некоторые общие резуль­таты теории установившегося притока однородной жидкости к подобным дренажным системам. Прежде всего, заметим, что известные аналогичные решения некоторых из подобных задач достаточно громоздки, а применяемые методы малоэффективны и не дают возможности их использования в решении родственных вопросов.

Решение соответствующих гидродинамических задач о зависимости притока жидкости от перепадов давления и геометрических
характеристик течения наталкивается на ряд трудностей аналитического порядка. Если имеется одна скважина или система параллельных неограниченно протяженных горизонтальных скважин, дренирующих однородный пласт ограниченной толщины, то задача решается наиболее просто. Точно так же сравнительно просто решается о притоке жидкости к системе, выполненной в форме «лучевых дрен», отходящих от центрального ствола в виде вертикальных трещин на всю мощность пласта.

Общее выражение расхода пластовой жидкости к некоторым системам наклонных скважин конечной длины, рассматриваемым как некоторые линейные источники с постоянной интенсивностью расхода жидкости по длине источника, найдено способом построения ньютонова потенциала точечного источника, действующего в пласте ограниченной мощности.

Заметим, что применяемый здесь способ аналитического исследования некоторых пространственных задач фильтрации достаточно широк для решения некоторых новых задач. Например, метод при­меним к исследованию притока жидкости из пласта ограниченной мощности к дискообразной трещине, имитирующей систему неогра­ниченно большого числа горизонтальных скважин, отходящих от центрального ствола [13].

Приток жидкости к наклонной скважине ограниченной длины в однородном горизонтальном пласте ограниченной толщины [11, 14, 16]. Пусть в горизонтальном однородном пласте, толщина которого равна h, а проницаемость к, наклонная скважина АСА' (рис. 1.6) длиной 2 образует угол с горизонтальной плоскостью Е; центр С прямолинейного отрезка АА' находится на высоте а₀ от подошвы Е пласта. Наклонную скважину АСА' представляем как некоторый канал в пористой среде пласта; к этому каналу происходит сток пластовой жидкости. Пусть отрезок АА' имитирует линейный сток с постоянной плотностью q = Q/2 расхода жидкости (Q — общий объемный расход жидкости в стоке). Линейный сток АА' заключен в некотором семействе изобарических поверхностей — замкнутых оболочек, одна из которых (оболочка S) имитирует за­бойную поверхность наклонной скважины АСА'. Предполагаем, что оболочка S достаточно тесно охватывает прямолинейный отре­зок АА'. На забойной по­верхности S задано рабочее давление р = р₀ = const [27, 28, 36, 9].

 

Рис. 1.6. Наклонная скважина конечной длины в пласте ограниченной мощности

 

Плоское сечение Е_о, про­веденное через центр С, перпендикулярно к оси АА' и образует замкнутую ли­нию Г на поверхности S. Средний радиус замкнутой линии Г примем за «рабо­чий» радиус r₀ наклонной скважины.

Положение наклонной скважины АСА' определяем в прямоугольной системе координат xyz, причем ось z направляем по вертикали через центр С. Начало координат О поместим в точке пересечения оси z с подошвой пласта. Плоскость xz проводим через отрезок АА'.

При таком выборе координатной системы относительно линей­ного стока (источника) естественно предположить, что вдали от него фильтрационный поток переходит асимптотически в осесимметричный. Примем, что на некоторой цилиндрической поверхности S_* с осью z и радиусом r_* (r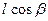_* > ) задано среднее значение давле­нии р=р_* = const. Эта величина представляет некоторый гидро­динамический эквивалент давления на «контуре питания».

Решение задачи о притоке жидкости к наклонной скважине в условиях установившегося потока несжимаемой жидкости нахо­дим при помощи потенциала скоростей. Для этого используем формулу [27,41]:

(1.18)

где K₀(t) - видоизмененная функция Бесселя нулевого порядка второго рода при t= .

Если под и понимать соответственно выражения:

 

(1.19)

 

то левую часть соотношения (1.18) истолковываем как значение потенциала Ф_к в точке М (r, , z) от точечного стока (или источника) с интенсивностью 4 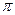, расположенного в точке М_о (), учитывая при этом обозначения ( = 0, ±1,..., ± ) и полагая, что числа (соответственно ) представляют цилиндрические координаты точки М (и точки М_о).

Потенциал всех 2 n +1 стоков (источников), дей­ствующих с одинаковыми интенсивностями потока q (расходы пла­стовой жидкости), на основании (1.18) записываем в виде:

 

. (1.20)

 

Суммирование под знаком интеграла по 0, ± 1,..., ± приводит выражение (1.20) к виду:

 

(1.21)

 

Здесь в отличие от зависимости (1.20) добавлена постоянная интегрирования С_n.

При фиксированном n и > 0 несобственный интеграл в выра­жении Ф_n (1.21), а также интеграл, получаемый из Ф_n дифференци­рованием по z под знаком интеграла, сходятся равномерно, поэтому справедлива зависимость:

(1.22)

Отсюда следует

. (1.23)

 

Первое из равенств (1.23) показывает, что плоскость Е (z = 0) представляет непроницаемую границу области D (подошва пласта) течения, определенного потенциалом Ф_n при любом n.

Второе из равенств (1.23) показывает, что плоскость Е' (z = h) представляет непроницаемую границу области D (кровля пласта) лишь при , то есть когда стоки (источники), находящиеся в точ­ках ±а, при построении соответствующего потенциала Ф_n берутся вместе со всеми своими зеркальными отражениями в плоскостях Е и Е'.

В выражении (1.21) нельзя сделать почленный предельный переход при . Это вызвано тем, что как интеграл, так и аддитивное постоянное С_n в выражении (1.21) расходятся при , поэтому конкретное применение (1.21) при требует преобразования правой части равенства (1.21). Этого можно достичь соответствующим исключением С_n из (1.21).

Пусть точки М(s) и определяют элементарный отрезок
ММ' на линейном стоке (источнике) АСА' (рис. 1.6). Обозначаем общий расход пластовой жидкости в линейном стоке (источнике) АСА' через Q. Тогда элементарный расход жидкости на отрезке ММ', то есть при условии , выражается формулой:

(1.24)

Элементарный потенциал от элементарного стока (источ­ника) ММ' и его 2n отражений в подошве и кровле пласта на осно­вании равенства (1.21) выражается в виде:

(1.25)

Суммируем все элементарные потенциалы (1.25) от стоков (источников), расположенных на отрезке АСА' и на всех их отраже­ниях (2n). Тогда получаем потенциал скоростей Ф_n от линейного стока АСА':

(1.26)

Здесь обозначено:

(1.27)

Используем зависимость (1.26) для установления соотношения между расходом Q и перепадом давления ; для этого полагаем, что значение потенциала определено на забойной поверхности S наклонной скважины в некоторой точке М_о () нормального сечения поверх­ности S, проведенного через точку С. Затем при помощи зависи­мости (1.26) выражаем среднее значение потенциала на цилиндрической поверхности S_* с радиусом и осью Оz. Для р₀ и р_* находим выражение:

(1.28)

(1.29)

при

(1.30)

 

Интеграл в выражении р_* вычисляем при помощи теоремы [5,23] сложения для функции К₀ (t):

(1.31)

при условии, что

и . (1.32)

 

На основании (1.26), (1.29) и (1.31) находим , затем величину р_* выражаем в виде:

 

(1.33)

 

Исключаем С_n из (1.28) и (1.33), тогда находим зависимость:

(1.34)

 

Под знаком двойного интеграла (1.34) функция выражается в виде:

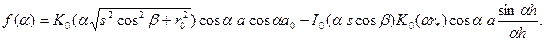(1.35)

Найдем предел (+0), используя для этого разложе­ния функций К_о (t) и I₀ (t) [5,23],

(1.36)

где С = 0,5772... — постоянная Эйлера.

Из выражений (1. 35) и (1. 36) следует

(1.37)

В равенстве (1.34) сделаем предельный переход, применяя при этом функциональное разложение:

(1.38)

 

где - непрерывная при а > 0 функция, удовлетворяющая условиям Дирихле и имеющая на бесконечности достаточный поря­док малости для сходимости интеграла (1. 38).

Учитывая выражения (1. 35) и принимая во внимание (1.37), из (1.34) и (1.38) получаем искомую формулу для притока несжимаемой жидкости к наклонной скважине АСА', дренирующей однородный пласт ограниченной мощности,

(1.39)

Здесь приняты следующие обозначения: 2 - длина наклонной скважины; - угол наклона скважины относительно горизонтальной плоскости, при этом необходимо соблюсти неравенства и ; - высота центра С наклонной скважины от подошвы пласта; h - мощность пласта; r₀ - радиус нормального сечения забойной поверхности скважины, проведен­ного через ее центр С; r_* - радиус прямого вертикального цилиндра S_*, ось которого проходит через центр С скважины; р₀ - забойное давление; р_* - давление среднее на поверхности прямого цилиндра S_*; Q - суммарный приток жидкости к наклонной сква­жине; к - проницаемость пористой среды; 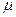- вязкость жидкости; К_о(t) - видоизмененная функция Бесселя нулевого порядка вто­рого рода.

Если в формуле (1.39) угол наклона оси скважины АСА' при­равнять нулю ( = 0), то получаем соотношение, которым опре­деляем приток Q жидкости к горизонтальной скважине, дрениру­ющей бесконечный однородный пласт постоянной мощности при условии, что фильтрационный поток вдали от такой горизонтальной скважины переходит асимптотически в осесимметричный поток. При этом предполагаем, что задано постоянное давление р₀ на поверх­ности S, имитирующей забойную поверхность скважины, и среднее пластовое давление р_* на некоторой цилиндрической поверхности S_* с радиусом r_* и осью Oz, окружающей наклонную скважину АСА'.

Соответствующая зависимость имеет вид:

 

. (1.40)

Встречающийся в выражении (1.40) ряд при упрощается [3] и получается достаточно точная, хотя и приближенная зависимость для притока жидкости Q:

(1.41)

Приток жидкости к симметричному кусту наклонных скважин одинаковой длины. Рассмотрим систему скважин из одина­ково наклонных к горизонтальной плоскости , имеющие длины ствола 2 , дренирующую горизонтальный однородный пласт, толщина которого равна h [28,29,31,6,58].

Предполагаем, что система CA_j (j = 1, 2,…, ) наклонных скважин образует симметричную систему «лучей», исходящих из общего центра С (рис. 1.7). Систему таких скважин назовем ку­стом С.

 

 

Рис. 1.7. Пара соседних наклонных стволов в кусте

из наклонных скважин

 

Наклонная скважина CA_j, входящая в состав куста С, предста­вляет собой некоторый канал в пористой среде пласта. Прямоли­нейный отрезок CA_j имитирует линейный сток с постоянной плотностью q=Q/2 расхода жидкости (Q - объемный расход жидкости отдельном линейном стоке CA_j). На основании симметрии в распо­ложении отдельных наклонных скважин в кусте заключаем, что величина Q будет одинакова для каждой из наклонных скважин куста С.

Пучок линейных стоков CA_j заключен в некотором семействе изобарических поверхностей, каждая из которых представляет некоторую замкнутую оболочку, содержащую в себе пучок С линейных источников CA_j. Одна из этих оболочек (S) имитирует забойную поверхность куста С наклонных скважин.

Предполагаем, что оболочка S достаточно тесно охватывает каждый из прямолинейных отрезков CA_j. На забойной поверхности S задано рабочее (среднее) давление р = р₀= const.

Проведем плоское сечение E_j оболочки S через середину от­резка CA_j и перпендикулярно к нему. Это сечение образует замкнутую линию Г_j на поверхности S. Средний радиус замкнутой линии Г_j принимаем за «рабочий» радиус r₀ наклон­ной скважины CA_j, входящей в состав куста С. Из соображений симметрии полагаем, что «рабочие» радиусы всех наклон­ных скважин одинаковы.

Положение наклонных сква­жин CA_j куста С определяем в цилиндрической системе координат , в которой ось z напра­вляем по вертикали через центр С.

Начало координат О помещаем в точке пересечения оси z с подошвой пласта. Проводим вертикальную плоскость через последнюю из занумерованных наклонных скважин, т. е. через отрезок CA_V. Горизонтальную полупрямую ОР, на которую проектируется отре­зок CA_V, принимаем за ось полярной системы координат z.

Проекции всех наклонных скважин CA_j на горизонтальную плоскость образуют некоторую систему лучей ОА_j с центром симме­трии в точке О. Положение каждого из этих лучей определяем по­лярным углом . Центр С куста наклонных скважин отно­сительно подошвы пласта определяем координатой . Точки A_j, представляющие концы наклонных скважин, определяем координатами ; на рис.1.7 принято а_*<а₀ при условии >0.

Вдали от куста фильтрационный поток переходит асимптотически осесимметричный; поэтому принимаем, что на некоторой цилиндрической поверхности S_* с осью z и радиусом r_* (r_*> 21cos ) задано среднее значение давления р = р_* = const. Эта величина представляет гидродинамический эквивалент давления на «контуре области питания».

Полу­чаем выражение потенциала Ф_n скорости фильтрации в точке М (, z) от линейных стоков СА_j, дренирующих однородный пласт с одинаковой линейной плотностью объемного расхода ,

(1.42)

 

Здесь обозначено:

 

(1.43)

(1.44)

 

Предварительно выражаем значение потенциала на забойной поверхности -й наклонной скважины, входящей в состав куста С. Для этого борем некоторую точку М на линии F_v нормального сечения забойной поверхности S_v. Затем при по­мощи зависимости (1.42) выражаем среднее значение потенциала на цилиндрической поверхности S _* с радиусом r_* и осью z. За точку М примем такую, у которой координаты r, z и имеют соответственно значения:

(1.45)

В результате последующего предельного перехода при с использованием функционального соотношения [21], получаем искомую формулу для притока несжимаемой жидкости к кусту С из наклонных скважин, дренирующих однородный пласт ограниченной мощности при 2,

(1.46)

Здесь приняты следующие обозначения:

(1.47)

(1.48)

- длина каждой наклонной скважины CA_j (j = 1, 2,…, ); - угол наклона каждой из скважин относительно горизонталь­ной плоскости; а₀ - высота центра С куста скважин от подошвы пласта; h - мощность пласта; r₀ - средний радиус нормального сечения забойной поверхности скважины, проведенного через ее центр; r_* - радиус прямого вертикального цилиндра S_*, ось которого проходит через центр С куста; р_о - забойное давле­ние, одинаковое на всех наклонных скважинах; р_* - среднее давление на поверхности прямого цилиндра S_*; Q - суммарный рас­ход жидкости в отдельной наклонной скважине; Q_o = Q - общий расход жидкости куста скважин; - проницаемость пористой среды; 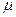- вязкость пластовой жидкости; К_о (t) - видоизмененная функция Бесселя нулевого порядка второго рода.

Если в формулах (1.46) - (1.48) принять = 0, то система наклонных скважин превращается в систему лучевых дрен с общим центром С: Тогда формула для притока жидкости из наклонных скважин примет вид

 

(1.49)

 

При

(1.50)

Приближенное решение задачи о притоке нефти к горизонтальным скважинам в однородном пласте. Рассмотрим горизонтальную скважину длиной l, радиуса r_c, расположенную в центре однородного изотропного пласта с круговым контуром питания радиуса R_k, на котором задано давление p_k (рис. 1.8). Давление на забое скважины p_c. Пласт и содержащуюся в нем жидкость предполагаем несжимаемыми.

 

Рис. 1.8. Горизонтальная скважина

 

Полное фильтрационное сопротивление можно представить суммой двух сопротивлений: внешнего – от контура питания до прямолинейной вертикальной галереи, совпадающей с проекциями горизонтальной скважины на кровлю (или подошву) пласта, и внутреннего, обусловленного тем, что мы имеем в действительности не галерею, а скважину [28,64].

Внешнее сопротивление определим по формуле:

. (1.51)

Внутреннее сопротивление определяем для одной вертикальной скважины в батарее, полагая, что толщина рассматриваемого пласта соответствует расстоянию между скважинами, а длина ствола горизонтальной скважины равна толщине пласта в случае вертикальной скважины. Тогда:

(1.52)

Эту же формулу можно получить, мысленно разрезав горизонтальную скважину на отрезки длиной, равной мощности пласта h, и повернув каждый из них до вертикального положения. При этом будем иметь батарею вертикальных скважин, расстояние между которыми равно h, а их число равно l/h.

Сумма указанных сопротивлений даст нам отношение перепада давления к дебиту горизонтальной скважины:

(1.53)

В случае n горизонтальных стволов, выходящих из одной точки в центре пласта при равенстве углов между ними (рис. 1.9), получим следующую расчетную формулу:

(1.54)

где l – длина отдельного ствола; æ=æ(n) – параметр, определяемый из табл. 1.1

Таблица 1.1

Таблица определения значения параметра æ

 

n
æ			1,86	1,78

 

Рис. 1.9. Схема многозабойно-горизонтальной скважины

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: