На нестационарных режимах фильтрации

Методы обработки результатов гидродинамиче­ских исследований горизонтальных и вертикальных скважин на стационарных режимах фильтрации во многом схожи между собой, поэтому первоначально результаты нестационарных гидродинамических исследований горизонтальных скважин пытались обрабатывать стандартными методами, предназначенными для вертикальных скважин. Этому способствовала первая теоретическая ра­бота в области моделирования нестационарных гидродинамических исследова­ний горизонтальных скважин, в которой был рассмотрен приток слабо сжимаемой жидкости к горизонтальной скважине, расположенной в пласте конечной толщины и с бесконечно удаленными боковыми границами. Решение соответ­ствующей задачи было получено в очень сложной форме. Простое и удобное уравнение притока было получено только для достаточно больших значений времени, и оно, естественно, не отражало влияния кровли и подошвы пласта на геометрию притока флюида в начальный период времени. Это уравнение по форме было аналогично стандартному уравнению нестационарного притока к вертикальной скважине и поэтому получило самое широкое распространение.

В дальнейшем было получено решение задачи о нестационарном притоке слабо сжимаемой жидкости к горизонтальной скважине в пласте с непроницае­мыми границами, которое позволило выявить три периода притока - начальный радиальный, переходный и псевдорадиальный. Наличие этих периодов свя­зано с влиянием границ пласта.

Аналитическими исследованиями установлено наличие четырёх периодов притока нефти к горизонтальной скважине в полностью изолированном пласте. Наличие этих периодов установ­лено и для горизонтальных газовых скважин. Каждый из этих режимов харак­теризуется своей геометрией притока (рис. 1.14).

 

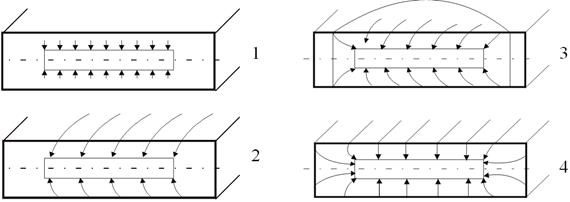
Рис. 1.14. Периоды притока флюида к горизонтальной скважине (1-4 – номера периодов)

1. В начальный период времени приток пластового флюида является радиальным в плоскости, перпендикулярной оси горизонтального ствола; этот период называется начальным радиальным и длится до тех пор, пока не начнёт проявляться влияние кровли и подошвы пласта.

2. Затем к радиальному притоку в той же плоскости присоединяется линейный поток в горизонтальной плоскости; этот период называется начальным линейным.

3.Следующий период отличается от предыдущего тем, что приток к горизонтальному стволу становится псевдорадиальным в плоскости простирания пласта и продолжается до тех пор, пока не начнёт проявляться влияние боковых границ пласта; этот период обычно называется заключительным радиальным.

4. Заключительный период характеризуется влиянием всех внешних границ пласта и обычно называется заключительным линейным.

Наличие этих периодов является причиной неприменимости обработки результатов гидродинамических исследований горизонтальных скважин при нестационарных режимах фильтрации методами, предназначенными для вертикальных скважин. Это объясняется тем, что в процессе исследований вертикальных скважин геометрия притока пластового флюида не изменяется.

 

Математические модели притока жидкости горизонтальных скважин. Представленная ниже методика расчёта параметров пласта по кривым восстановления давления в горизонтальных скважинах основана на использовании математической модели уравнения фильтрации любого однофазного флюида,

 

(1.67)

где к_х, к_у, к_z - проницаемости по осям x,y,z; m - пористость.

Рассмотрим случай, когда пласт представляет собой параллелепипед с непроницаемыми стенками. Горизонтальная скважина длиной l пройдена в направлении оси х, толщина пласта - h, длина пласта по оси у равна а, а по оси х - " b ". Считается, что скважина в течение времени t рабо­тала с постоянным массовым дебитом q_m, а затем была мгновенно закры­та, время восстановления давления - . Для рассматриваемого случая решение задачи было получено методами теории теплопроводности в виде беско­нечных тригонометрических рядов, что делало его совершенно негодным. Однако в последствии с его помощью было выявле­но четыре периода притока слабо сжимаемой жидкости к горизонтальному стволу нефтяной скважины, для каждого из которых были получены про­стые и удобные выражения. В работе автора они были преобразованы для описания притока жидкости к горизонтальной скважине. В случае восстановления давления эти выражения имеют вид:

1. Период начального радиального притока в вертикальной плоскости

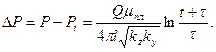(1.68)

 

2. Период начального линейного притока

(1.69)

 

3. Период псевдорадиального притока в горизонтальной плоскости

 

(1.70)

 

4. Период заключительного притока

 

(1.71)

 

Здесь t - время работы скважины с постоянным массовым дебитом Q; - время восстановления давления; P_i, Р - начальное и текущее псевдодавления в горизонтальном стволе.

Методы интерпретации кривых восстановления давления в горизонтальных скважинах. Интерпретация кривых восстановления давления может быть реализована на основе интегрированной модели процесса, т.е. аналитического ре­шения в самой общей форме. Однако в этом случае в процессе адаптации расчетных данных к реальным значениям потребуется многократное реше­ние задачи и создание специальных компьютерных программ. Кроме того, в случае применения интегрированной модели приходится считаться с не единственностью решения задачи и возможностью появления ложных ре­зультатов интерпретации даже при хорошем приближении к реальным дан­ным испытаний скважины. Поэтому ниже будет использован сегментный подход, при котором уравнение восстановления давления записывается для каждого периода притока флюида к горизонтальному стволу. В соответствии с предлагаемой методикой обработку кривой восстановления давления необходимо начинать с выделения периодов притока на основе уравнений восстановления давления (1.68 - 1.71). В частности периоды радиального притока выделяются после обработки данных в координатах , а линейного при­тока , где р - давление в горизонтальном стволе; Z -коэффициент сверхсжимаемости газа; t - время работы скважины до её ос­тановки; - время восстановления давления после остановки скважины. Наличие и время существования каждого периода определяется по нали­чию и размерам прямолинейного участка на кривых восстановления дав­ления в соответствующих координатах. После выде­ления периодов течения можно начать определение параметров пласта по следующим формулам:

 

1-й период:

(1.72)

2-й период:

(1.73)

3-й период:

(1.74)

4-й период:

(1.75)

 

Здесь l - длина работающего интервала горизонтального ствола, k_х,k_y, k_z - проницаемости вдоль осей координат; 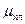- динамическая вязкость газа в пластовых условиях, T_пл,T_aт, р_пл, р_ат - температура и давление газа в пластовых и атмосферных условиях; Q_aт - объёмный дебит газа, приведенный к атмосферным условиям; - угол наклона прямолинейного участка кривой восстановления давления к оси абсцисс, то есть времени; n - номер периода притока; h - работающая толщина пласта; m -пористость; b - размер залежи в направлении оси горизонтального ствола.

Неустановившийся приток к двухзабойной горизонтальной скважине в пласте с подошвенной водой. [28] Рассматривается работа горизонтальной скважины в тонком нефтя­ном пласте, подстилаемом подошвенной водой. Работа такой скважины мо­жет быть осложнена быстрым прорывом подошвенной воды. Для предотвращения прорыва воды ниже водонефтяного контакта можно расположить еще один горизонтальный ствол для одновременно-раздельного отбора воды и нефти (рис. 1.15). Способы технической реализации режима одновре­менно-раздельного отбора нефти и воды известны, и, в частности, нефть может отбираться по насосно-компрессорным трубам, а вода по затрубному пространству. Возникает задача расчета дебитов стволов при совместной их работе для достижения неподвижности водонефтяного контакта.

 

Рис. 1.15. Схема расположения горизонтальных стволов

в водонефтяной залежи

 

Задача решается при условии, что месторождение разрабатывается рядами горизонтальных скважин при наличии нагнетательных рядов скважин. Таким образом, каждая добывающая скважина работает в полосообразном элементе пласта с двусторонним контуром питания (рис. 1.16).

 

Рис. 1.16. Элемент пласта с горизонтальной скважиной

между линиями нагнетания

При неподвижности водонефтяного контакта на нем должно выполняться условие (1.59). Так как водонефтяной контакт принимается неподвижным, то можно считать его непроницаемой границей, а для нахождения давления Р_А как со стороны нефти, так и со стороны воды достаточно решить уравнение пьезопроводности отдельно для верхнего и нижнего ствола.

Для верхнего ствола решение уравнения пьезопроводности для безразмерной депрессии находится с использованием метода функций Грина и имеет вид [28]:

(1.76)

Здесь введены следующие безразмерные величины:

(1.77)

где и - пьезопроводность по горизонтали и вертикали для нефтенасыщенной части пласта; X_s и Y_s - соответственно длина и ширина полосы (рис. 1.15); С_с, Y_c, Z_c - координаты середины ствола скважины; L - длина горизонтального ствола скважины; X, Y, Z - координаты точки, в которой рассчитывается безразмерное давление, остальные обозначения общепринятые.

Для нижнего ствола, находящегося в водонасыщенной части пласта, решение выглядит аналогично. Разница лишь в том, что вместо в (1.76) и (1.78) следует подставить соответствующие параметры для воды 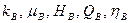и вертикальную координату .

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: