 |
Численное моделирование и интерпретация
|
|
|
|
ПОЛУЧЕННЫХ ДАННЫХ
При проведении численных расчетов были использованы результаты испытаний скважин Покачёвского месторождения. Рассмотрим слоистый пласт круговой и полосовой залежи. Для расчетов использованы следующие данные. Пусть Rк=500 м, k =0,1 Д, h =15 м, 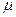 =2мПа·с, r c=0,1 м, r1= 26 м (при
=2мПа·с, r c=0,1 м, r1= 26 м (при  =60о) и r 1=85 м (при
=60о) и r 1=85 м (при  =80о),
=80о), 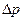 = рк-рс= 3 МПа. Вычислим дебит многозабойной скважины для 2, 3 и 4 забоев по формулам (1.6), (1.7). Результаты расчета приведены в табл. 2.1.
= рк-рс= 3 МПа. Вычислим дебит многозабойной скважины для 2, 3 и 4 забоев по формулам (1.6), (1.7). Результаты расчета приведены в табл. 2.1.
Таблица 2.1
Результаты расчета дебита при различных количествах забоев
| n | r1, м | Q, т/сутки |
| 176,57 215,44 | ||
| 204,82 263,36 | ||
| 221,15 293,7 |
По результатам вычислений можно построить зависимости дебита от числа забоев и угла наклона скважин, которые отображены на рис. 2.1.

(количество стволов)
Рис. 2.1. Зависимость дебита от количества забоев
Из графиков видно, что с увеличением числа забоев, дебит скважин растет. Если в случае двухзабойной скважин при  =60о дебит равен 70,6 т/сутки, то в случае четырехзабойной скважины он составляет 88,4 т/сутки.
=60о дебит равен 70,6 т/сутки, то в случае четырехзабойной скважины он составляет 88,4 т/сутки.
Построена зависимость дебита от угла наклона скважин. Показано, что если рассмотреть скважину с двумя забоями, то разница значения дебита равна 5,5 т/сутки, а в случае четырех забоев – уже 29 т/сутки, то есть чем больше угол наклона, тем скважина более эффективна.
Зависимость дебита Q от депрессии 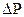 приведена на рис. 2.2.
приведена на рис. 2.2.

ΔP (депрессия), МПа
Рис. 2.2. График зависимости дебита от депрессии
Из графика видно, что с увеличением количества забоев продуктивность скважины возрастает. Так коэффициент продуктивности для двухзабойной скважины составляет 58,86 т/сутки·МПа, для трехзабойной – 68,3 т/сутки·МПа, а для четырехзабойной – 73,7 т/сутки·МПа.
|
|
|
Ниже на рис. 2.3 приведено трехмерное изображение зависимости дебита Q от депрессии 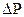 и от числа забоев скважины при угле наклона 80о.
и от числа забоев скважины при угле наклона 80о.
|
|
|
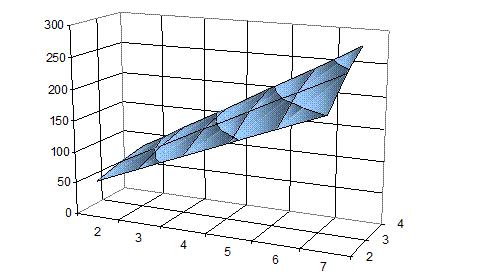
Рис. 2.3. Зависимость дебита от депрессии и числа забоев
На рис. 2.4 изображена зависимость гидропроводности ( ) от депрессии
) от депрессии 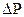 при двух, трех и четырех забоях.
при двух, трех и четырех забоях.
|
|
|
|
|

Рис. 2.4. Зависимость гидропроводности пласта от депрессии
Из графика видно снижение гидропроводности при увеличении депрессии. Также видно, что с ростом числа стволов величина  увеличивается. Так, например, значение гидропроводности при депрессии 3МПа и четырех забоях на 26% больше, чем в скважине с двумя забоями.
увеличивается. Так, например, значение гидропроводности при депрессии 3МПа и четырех забоях на 26% больше, чем в скважине с двумя забоями.
Зависимость подвижности  от депрессии
от депрессии  при различных значениях толщины пласта h приведена на рис. 2.5 в трехмерном пространстве.
при различных значениях толщины пласта h приведена на рис. 2.5 в трехмерном пространстве.
|
|
|

Рис. 2.5. Зависимость подвижности от депрессии
при различных значениях толщины пласта
Из графика видно, что чем больше толщина пласта, тем меньше подвижность. Так же, как отмечалось выше, при увеличении депрессии подвижность резко уменьшается.
Ниже приводятся результаты расчета дебита ГС в случае слоистого тонкого пласта. При расчетах использованы следующие исходные данные: Rк =1000 м, k =0,1 Д, h =30 м, 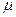 =2 мПа·с, а =100 м,
=2 мПа·с, а =100 м, 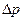 = рк-рс= 3МПа. Дебиты горизонтальных скважин вычислены по формулам (1.13), (1.15), (1.16) для двухзабойной, трехзабойной и четырехзабойной скважин приведены в табл. 2.2.
= рк-рс= 3МПа. Дебиты горизонтальных скважин вычислены по формулам (1.13), (1.15), (1.16) для двухзабойной, трехзабойной и четырехзабойной скважин приведены в табл. 2.2.
Таблица 2.2
Результаты расчета дебита при различных количествах забоев
| n | Q т/сутки |
| 652,37 | |
| 668,56 | |
| 678,77 |
Исследуем зависимость дебита от длины ствола многозабойной скважины (рис. 2.6). Расчеты выполнены при вариации длины стволов от 50 м до 500 м для случаев двух, трех и четырех забоев.

длина ствола, м
Рис. 2.6. Зависимость дебита скважины от длины стволов
|
|
|
Как видно из графика, дебит многозабойной скважины значительно растет при увеличении длины ствола. Это объясняется увеличением фильтрационной поверхности ствола, так как вся длина ствола лежит в продуктивной части пласта.
Зависимость дебита многозабойной скважины от депрессии приведена на рис. 2.7. Из рисунка видно, что дебиты скважин практически равны: при n =2 кпрод =217,5 т/сутки·МПа, при n =3 кпрод =222,8 т/сутки·МПа, при n =4 кпрод =226,3 т/сутки·МПа.

ΔP (депрессия), МПа
Рис. 2.7. Зависимости дебита скважины от депрессии
Ниже приведена 3D визуализация зависимости дебита Q от депрессии 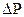 при различных длинах ствола скважин (рис. 2.8).
при различных длинах ствола скважин (рис. 2.8).
|
|
|

Рис. 2.8. Зависимости дебитаот депрессии
и длины горизонтального ствола скважины
На рис. 2.9 приведена зависимость гидропроводности ( ) от депрессии
) от депрессии 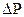 при двух, трех, четырех забоях.
при двух, трех, четырех забоях.
|
|
|
|
|

Рис. 2.9. Зависимости гидропроводности пласта от депрессии
Из рисунка видно, что гидропроводность пласта практически одинакова для всех случаев, то есть не зависит от числа забоев.
3D визуализация зависимости подвижности пласта от депрессии при различных значениях толщины пласта приведена на рис. 2.10.
|
|
|
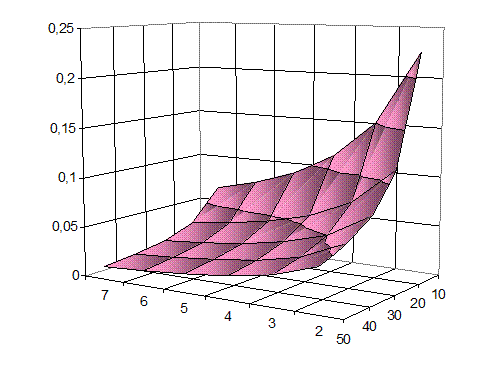
Рис. 2.10. Зависимости гидропроводности от депрессии
при различных значениях толщины пласта
Из графика видно, что чем больше толщина пласта, тем меньше подвижность. Так же, как отмечалось выше, при увеличении депрессии подвижность резко уменьшается.
Ниже приведены результаты расчетов дебита многозабойной скважины при установившемся притоке в однородном пласте. Использованы следующие исходные данные: Rк=1000 м, k =0,1 Д, h =30 м, 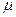 =2 мПа·с, а = 100 м,
=2 мПа·с, а = 100 м, 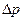 = рк-рс= 3 МПа. Проведены вычисления дебитов скважин при двух, трех и четырех забоях по формуле (1.54). Полученные значения сведены в табл. 2.3.
= рк-рс= 3 МПа. Проведены вычисления дебитов скважин при двух, трех и четырех забоях по формуле (1.54). Полученные значения сведены в табл. 2.3.
Таблица 2.3
Результаты расчета дебита при различных количествах забоев
| n | Q, т/сутки |
| 546,6 | |
| 590,5 | |
| 616,7 |
Зависимость дебита скважин от депрессии приведены на рис. 2.11.

ΔP (депрессия), МПа
Рис. 2.11. Зависимости дебита скважины от депрессии
Как видно из полученных зависимостей, большему числу забоев соответствует большее значение дебитов. Например, в случае для двух, трех и четырех забоев дебиты скважин составили 182,2 т/сутки·МПа; 196,8 т/сутки·МПа; 205,6 т/сутки.
|
|
|
Зависимость дебита Q от длины ствола L в однородном пласте приведена на рис. 2.12. Расчеты дебита вычислены, варьируя длины ствола скважины, при прочих равных условиях. Так при L =100 м четырехзабойной скважины дебит Q равен 616,7 т/сутки, а при L =400 м дебит возрастает до 1248,5 т/сутки, что на 50% больше предыдущего результата.

длина ствола, м
Рис. 2.12. Зависимости дебита скважины от длины ствола
Ниже приведен график зависимости дебита скважины от депрессии 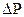 при различных длинах горизонтального ствола скважин в трехмерном пространстве (рис. 2.13).
при различных длинах горизонтального ствола скважин в трехмерном пространстве (рис. 2.13).
|
|
|

Рис. 2.13. Зависимости дебита от депрессии при различных длинах стволов
Зависимость подвижности однородного пласта от депрессии для различных значений толщины пласта приведена на рис. 2.14. Из графика видно, что чем больше толщина пласта, тем меньше подвижность. Так же, как отмечалось выше, при увеличении депрессии подвижность резко уменьшается.
|
|
|

Рис. 2.14. Зависимости гидропроводности от депрессии
при различных значениях толщины пласта
Практическую применимость предлагаемой методики интерпретации кривых восстановления давления горизонтальных скважин покажем на примере скважины, пробуренной на восточном участке Оренбургского ГКМ. Основополагающей причиной применения горизонтальных скважин для разработки данного объекта является низкая проницаемость коллекторов. По данным керна средняя величина открытой пористости коллекторов участка равна т =0,1, абсолютная проницаемость к =2,13×10-15 м2, при этом коллектора с проницаемостью до 10-15 м2 составляют 49,6%. По данным бурении, длина условно горизонтального ствола равна 435 м, эффективная толщина пласта коллектора 35,6 м, длина работающего интервала горизонтального ствола 84 м. Динамическая вязкость в пластовых условиях 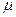 =0,015 мПа·с, Тпл =303 К, Тат =293 К, рат =0,0980665 МПа, рпл =16,52 МПа. Перед закрытием скважина работала в течение t =7сут=604800с с постоянным дебитом Qат =319,1 тыс.м3/сут. Исходные данные для обработки кривой восстановления давления представлены в табл. 2.4.
=0,015 мПа·с, Тпл =303 К, Тат =293 К, рат =0,0980665 МПа, рпл =16,52 МПа. Перед закрытием скважина работала в течение t =7сут=604800с с постоянным дебитом Qат =319,1 тыс.м3/сут. Исходные данные для обработки кривой восстановления давления представлены в табл. 2.4.
|
|
|
Таблица 2.4
Исходные данные для обработки результатов нестационарных
гидродинамических исследований горизонтальных скважин
 , с , с
| 
| 
| Рзаб, МПа | 
|  , с , с
| 
| 
| Рзаб, МПа | 
|
| - | 777,7 | 11,59 | 17033,8 | 1,863 | 691,4 | 15,19 | 29259,1 | ||
| 5,083 | 775,5 | 11,02 | 15399,5 | 1,82 | 687,2 | 15,41 | 30112,7 | ||
| 4,782 | 774,5 | 11,45 | 16624,8 | 1,78 | 683,2 | 15,44 | 30230,1 | ||
| 4,606 | 773,8 | 11,97 | 18169,1 | 1,744 | 679,4 | 15,57 | 30741,3 | ||
| 4,481 | 773,2 | 11,6 | 17063,2 | 1,711 | 675,8 | 15,62 | |||
| 4,305 | 772,2 | 11,71 | 17388,4 | 1,68 | 672,4 | 15,62 | |||
| 4,18 | 771,4 | 11,71 | 17388,4 | 1,652 | 15,76 | 31496,1 | |||
| 4,004 | 11,74 | 17477,6 | 1,625 | 665,8 | 15,8 | 31656,2 | |||
| 3,703 | 766,8 | 11,92 | 18017,6 | 1,576 | 659,8 | 15,89 | 32017,9 | ||
| 3,526 | 764,4 | 12,03 | 18351,7 | 1,532 | 654,1 | 15,89 | 32017,9 | ||
| 3,305 | 760,6 | 12,18 | 18812,2 | 1,493 | 648,7 | 16,04 | 32625,2 | ||
| 3,004 | 753,6 | 12,59 | 1,457 | 643,7 | 16,17 | 33156,2 | |||
| 2,828 | 748,3 | 12,79 | 20743,7 | 1,424 | 638,8 | 16,23 | 33402,7 | ||
| 2,703 | 743,8 | 13,37 | 22667,7 | 1,393 | 634,2 | 16,41 | 34147,7 | ||
| 2,528 | 736,4 | 13,38 | 22701,6 | 1,365 | 629,8 | 13,96 | 24712,4 | ||
| 2,403 | 730,2 | 13,74 | 23939,7 | 1,338 | 625,6 | 16,54 | 34690,9 | ||
| 2,307 | 724,8 | 14,03 | 24960,9 | 1,29 | 617,6 | 16,61 | 34985,2 | ||
| 2,216 | 719,2 | 14,31 | 25967,1 | 1,247 | 610,2 | 16,67 | 35238,4 | ||
| 2,104 | 711,5 | 14,71 | 27439,1 | 1,208 | 603,2 | 16,74 | 35534,9 | ||
| 2,03 | 705,8 | 14,85 | 27963,9 | 1,173 | 596,6 | 16,8 | 35790,1 | ||
| 1,967 | 700,7 | 14,88 | 1,141 | 590,4 | 16,84 | 35960,8 | |||
| 1,912 | 695,9 | 15,05 | 28722,2 | 1,112 | 584,5 | 16,95 | 36432,1 |
На рис. 2.15 – 2.17 представлены кривые восстановления забойного давления для отдельных периодов притока.

Рис. 2.15. Кривая восстановления давления
для начального радиального притока

Рис. 2.16. Кривая восстановления давления
для начального линейного притока
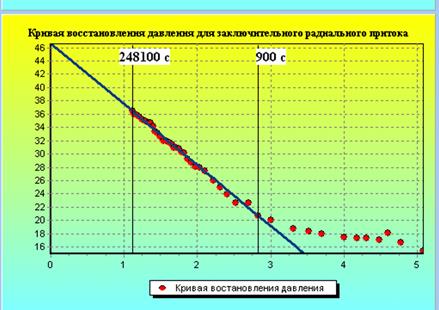
Рис. 2.17. Кривая восстановления давления
для заключительного радиального притока
Первым результатом обработки кривой восстановления давления является определение продолжительности периодов притока: 1-й период (начальный радиальный приток в вертикальной плоскости) длился от 5 до 30 с, 2-й период (начальный линейный приток) – от 40 до 900 с, 3-й период (псевдорадиальный приток в плоскости простирания плата) от 900 до 50700с и далее, поскольку по результатам испытаний он не закончен, 4-й период не выявлен вследствие недостаточной продолжительности испытания.
Как и следовало ожидать, 1-й период выражен нечётко и характеризуется большим разбросом точек, что объясняется влиянием объема ствола скважины. Как видно из рис. 2.17, наиболее представительным является третий период. Тангенс угла наклона прямолинейного участка для этого периода равен 9,2×103. Тогда из формулы (1.74) получаем  3×10-15. С достаточной долей уверенности можно принять kх = ky = kh, поэтому hkh = 3×10-15 м3. Тогда значение работающей толщины пласта составит 30 м, что полностью соответствует данным бурения.
3×10-15. С достаточной долей уверенности можно принять kх = ky = kh, поэтому hkh = 3×10-15 м3. Тогда значение работающей толщины пласта составит 30 м, что полностью соответствует данным бурения.
|
|
|
Тангенс угла наклона прямолинейного участка кривой на рис. 2.16 (второй период) равен 150. Тогда в соответствии с формулой (1.73) получаем  48,28×10-7 м3. Подставим в полученное выражение значение проницаемости 10-15 м2, тогда ориентировочное значение работающей длины горизонтального ствола составит около 160 м, что значительно меньше общей длины ствола.
48,28×10-7 м3. Подставим в полученное выражение значение проницаемости 10-15 м2, тогда ориентировочное значение работающей длины горизонтального ствола составит около 160 м, что значительно меньше общей длины ствола.
Обработка данных для первого периода производится с использованием формулы (1.72) аналогично 3-му периоду, поскольку в обоих случаях приток является радиальным. В этом случае имеем  6,17 ×10-14 м3.
6,17 ×10-14 м3.
Р А З Д Е Л IV
|
|
|



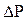 , МПа
, МПа


