 |
Рекомендации по организации выполнения
|
|
|
|
А.Д. Омарова
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К контрольной работе №2
По дисциплине
«Математика»
для студентов специальностей:
Подвижной состав железных дорог»
Эксплуатация железных дорог»
Наземные транспортно-технологические средства»
Системы обеспечения движения поездов»
Строительство железных дорог, мостов и транспортных тоннелей»
Менеджмент»
Минеральные Воды
Г.
А.Д. Омарова
Методические указания к Контрольной работе №1 по дисциплине «Математика» / Омарова А.Д. – Минеральные Воды: Филиал ФГБОУ ВПО РГУПС в г. Минеральные Воды, 2015. – 52 с.
Методические указания к контрольной работе №1 для студентов очной и заочной форм обучения специальностей:190300.65 Подвижной состав железных дорог, 190401.65 Эксплуатация железных дорог,23.05.01 «Наземные транспортно-технологические средства», 23.05.05 «Системы обеспечения движения поездов», 23.05.06 «Строительство железных дорог, мостов и транспортных тоннелей», 38.03.02 «Менеджмент».
Методические указания содержат задания к контрольной работе, теоретический материал и примеры решения типовых задач.
Методические указания рекомендованы к использованию в учебном процессе кафедрой «Естественнонаучные и инженерные дисциплины».
Ó Омарова А.Д.
Ó Филиал Ростовского государственного университета путей сообщения в г. Минеральные Воды, 2015
СОДЕРЖАНИЕ
| 1. Формулировка задания и его объем…………………….. | |
| 2. Общие требования к написанию контрольной рабОТы………….................................................................................... | |
| 3. Рекомендации по организации выполнения контрольной работы……………………………………………… | |
| 3.1. Неопределенный интеграл………………………………………… | |
| 3.2. Определенный интеграл……………………………..……………… | |
| 3.3. Дифференциальные уравнения…………………………….……… | |
| 3.4. Системы обыкновенных дифференциальных уравнений………… | |
| 3.5 Числовые ряды………………………………………………………. | |
| 3.6 Степенные ряды……………………………………………………… | |
| 3.7 Ряды Фурье………………………………………………….………. | |
| 4. Порядок защиты и ответственность студента за выполнение контрольной работы………………………. | |
| 5. Список рекомендуемой литературы……………………. |
|
|
|
Формулировка задания и его объём
Задача 1. Найти неопределенные интегралы.
1. 
| 2. 
|
3. 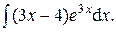
| 4. 
|
5. 
| 6. 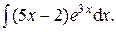
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 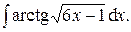
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 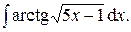
|
17. 
| 18. 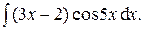
|
19. 
| 20. 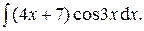
|
Задача 2. Найти неопределенные интегралы.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 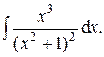
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 3. Найти неопределенные интегралы.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 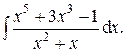
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 4. Найти неопределенные интегралы.
1. 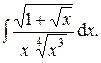
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 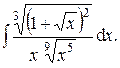
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 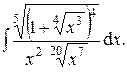
|
Задача 5. Вычислить определенный интеграл.
1.  . .
| 2.  . .
| 3.  . .
| 4.  . .
|
5.  . .
| 6.  . .
| 7.  . .
| 8.  . .
|
9.  . .
| 10.  . .
| 11.  . .
| 12.  . .
|
13.  . .
| 14.  . .
| 15.  . .
| 16.  . .
|
17. 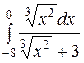 . .
| 18.  . .
| 19.  . .
| 20.  . .
|
Задача 6. Вычислить определенные интегралы.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 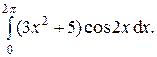
| 10. 
|
11. 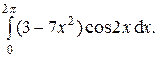
| 12. 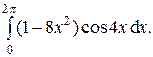
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 7. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
1. 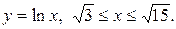
| 2. 
| |
3. 
| 4. 
| |
5. 
| 6. 
| |
7. 
| 8. 
| |
9. 
| 10. 
| |
11. 
| 12. 
| |
13. 
| 14. 
| |
15. 
| 16. 
| |
17. 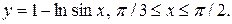
| 18. 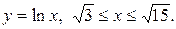
| |
19. 
| ||
20. 
| ||
Задача 8. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.
| 1. 3x2–4y=0, 2x–4y+1=0. | 11. y=x3+3, x=0, y=x–1, x=2. |
| 2. 3x2+4y=0, 2x–4y+1=0. | 12. y=x3+2, x=0, y=x–2, x=2. |
| 3. 2x+3y2=0, 2x+2y+1=0. | 13. y=x3+1, x=0, y=x–3, x=2. |
| 4. 3x2–4y=0, 2x+4y–1=0. | 14. y=x3–1, x=0, y=x–5, x=2. |
| 5. 3x2+4y=0, 2x+4y+1=0. | 15. y=x3–2, x=0, y=x–6, x=2. |
| 6. 2x–3y2=0, 2x+2y1=0. | 16. y=x3+3, x=0, y=x+7, x= –2. |
| 7. 3x2–2y=0, 2x-2y+1=0. | 17. y=x3+2, x=0, y=x+6, x= –2. |
| 8. 4x+3y2=0, 4x+2y+1=0. | 18. y=x3+1, x=0, y=x+5, x= –2. |
| 9. 3x2–2y=0, 2x+2y–1=0. | 19. y=x3–1, x=0, y=x+3, x= –2. |
| 10. 4x–3y2=0, 4x+2y–1=0. | 20. y=x3–2, x=0, y=x+2, x= –3. |
Задача 9. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде  ).
).
|
|
|
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 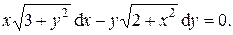
|
7. 
| 8. 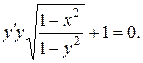
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 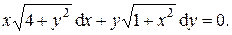
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 10. Найти общий интеграл дифференциального уравнения.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 11. Найти решение задачи Коши.
1. 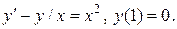
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 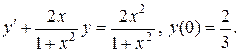
|
11. 
| 12. 
|
13. 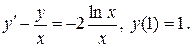
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 12. Найти общее решение дифференциального уравнения.
1. 
| 2. 
|
3. 
| 4. 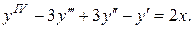
|
5. 
| 6. 
|
7. 
| 18. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 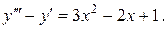
| 16. 
|
17. 
| 18. 
|
19. 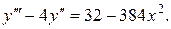
| 20. 
|
Задача 13. Найти общее решение системы дифференциальных уравнений.
1. 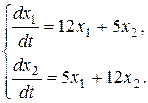 2.
2.  3.
3. 
4.  5.
5.  6.
6. 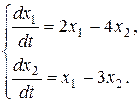
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17. 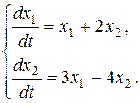 18.
18. 
19.  20.
20. 
Задача 14. Исследовать на сходимость ряд.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 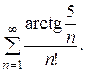
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 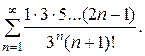
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 15. Исследовать на сходимость ряд.
1. 
| 2. 
|
3. 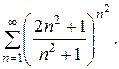
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
2.9. 
| 2.10. 
|
11. 
| 12. 
|
13. 
| 14. 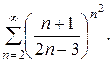
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 16. Исследовать на сходимость ряд.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 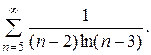
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
Задача 17. Исследовать на сходимость ряд.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 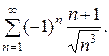
|
Задача 18. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.
1.  2.
2.  3.
3. 
4.  5.
5. 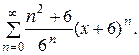 6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17.  18.
18. 
19.  20.
20. 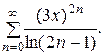
Задача 19. Представить периодическую функцию f(x), заданную на полупериоде 
 , рядом Фурье по синусам или косинусам. Построить график функции.
, рядом Фурье по синусам или косинусам. Построить график функции.
1.  по косинусам.
по косинусам.
2.  по синусам.
по синусам.
3.  по косинусам.
по косинусам.
4.  по синусам.
по синусам.
5.  по косинусам.
по косинусам.
6.  по синусам.
по синусам.
7.  по косинусам.
по косинусам.
8.  по синусам.
по синусам.
9.  по косинусам.
по косинусам.
10.  по синусам.
по синусам.
11.  по синусам.
по синусам.
12.  по косинусам.
по косинусам.
13.  по синусам.
по синусам.
14.  по косинусам.
по косинусам.
15. 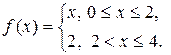 по синусам.
по синусам.
16. 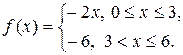 по косинусам.
по косинусам.
17.  по синусам.
по синусам.
18.  по косинусам.
по косинусам.
19.  по синусам.
по синусам.
|
|
|
20.  по косинусам.
по косинусам.
Общие требования к написанию
Контрольной работы
1. Контрольная работа выполняется от руки в обычной тетради для работ по математике или в печатном виде.
2. Решенное задание должно строго соответствовать присвоенному Вам варианту.
3. Перед решением необходимо переписать общее задание и задание Вашего варианта. По окончании решения записывается полученный ответ.
Рекомендации по организации выполнения
контрольной работы, примерный календарный план еЕ выполнения
Неопределенный интеграл
1. Определение. Неопределенным интегралом от функции y = f(x) называется выражение вида  . Функция F(x) называется первообразной для заданной функции f(x).
. Функция F(x) называется первообразной для заданной функции f(x).
При интегрировании наиболее часто используются следующие методы:
1) Если

где a и b – некоторые постоянные.
2) Подведение под знак дифференциала:
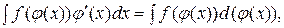
так как 
3) Формула интегрирования по частям:

Обычно выражение dv выбирается так, чтобы его интегрирование не вызывало особых затруднений. Зa u, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемым по частям, относятся, в частности функции вида P(x)eax, P(x)sinax, P(x)cosax, P(x)lnx, P(x)arcsinx, P(x)arctgx, где P(x) – многочлен от x.
4) Интегрирование радиальных дробей  сводится к разложению подынтегральной функции на элементарные дроби:
сводится к разложению подынтегральной функции на элементарные дроби:
а) корни Qn(x) простые вещественные:
 ;
;
б) среди корней знаменателя есть кратные:
 ;
;
в) среди корней знаменателя есть комплексные:
 .
.
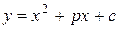 – не имеет действительных корней.
– не имеет действительных корней.
5) Интегрирование тригонометрических выражений.
1. Интегрирование выражений  .
.
С помощью «универсальной» подстановки  интегралы от функций
интегралы от функций  приводятся к интегралам от рациональных функций новой переменной t. Действительно, подставляя в подынтегральное выражение
приводятся к интегралам от рациональных функций новой переменной t. Действительно, подставляя в подынтегральное выражение  , получаем:
, получаем:
 .
.
Если подынтегральная функция имеет специальный вид, то лучше применять подстановки, требующие меньше вычислений:
1. Если  , то применяем подстановку
, то применяем подстановку  . Действительно, подынтегральное выражение приобретает вид
. Действительно, подынтегральное выражение приобретает вид
 .
.
2. Если 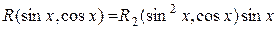 , то применяем подстановку
, то применяем подстановку  . Действительно, подынтегральное выражение приобретает вид
. Действительно, подынтегральное выражение приобретает вид
|
|
|
 .
.
3. Если 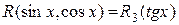 , то применяем подстановку
, то применяем подстановку  . Действительно, подынтегральное выражение приобретает вид
. Действительно, подынтегральное выражение приобретает вид
 .
.
4. Если  или
или
 , то применяем подстановку
, то применяем подстановку 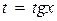 , тогда:
, тогда:
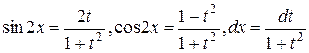 ,
,
или
 .
.
2. Интегрирование выражений  .
.
Для решения данных тригонометрических выражений необходимо применять формулы понижения степени:

до тех пор, пока не придем к табличным интегралам или к интегралам, которые известным образом сводятся к табличным.
3. Интегрирование выражений 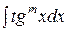 ,
,  .
.
Для решения данных тригонометрических выражений необходимо применять формулы:  .
.
4. Интегрирование выражений
 ,
,  ,
,  .
.
Для решения данных тригонометрических выражений необходимо применять формулы:

2. Таблица основных интегралов:
1. 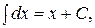
| 1. 
|
2. 
| 2. 
|
3. 
| 3. 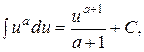
|
4. 
| 4. 
|
5. 
| 5. 
|
6. 
| 6. 
|
7. 
| 7. 
|
8. 
| 8. 
|
9. 
| 9. 
|
10. 
| 10. 
|
11. 
| 11. 
|
12. 
| 12. 
|
13. 
| 13. 
|
14. 
| 14. 
|
15. 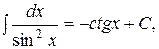
| 15. 
|
16. 
| 16. 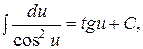
|
17. 
| 17. 
|
18. 
| 18. 
|
19. 
| 19. 
|
20. 
| 20. 
|
21. 
| 21. 
|
22. 
| 22. 
|
23. 
| 23. 
|
24. 
| 24. 
|
25. 
| 25. 
|
26. 
| 26. 
|
При внешней схожести формул в столбцах таблицы, следует понимать, что x это переменная интегрирования, а u – некоторая функция.
Пример 1. Найти  .
.
Решение. Так как  , то, используя формулы
, то, используя формулы


