 |
Системы обыкновенных дифференциальных уравнений
|
|
|
|
Система дифференциальных уравнений вида
где х 1, х 2, …, х n – неизвестные функции независимой переменной t, называется нормальной системой.
Пусть дана система n линейных дифференциальных уравнений с постоянными коэффициентами:
Эту систему можно записать в виде одного матричного дифференциального уравнения 
, где
Решение системы ищем в виде 
, 
, …, 
. Подставив значения 
в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно 
:
Система должна иметь ненулевое решение, поэтому для определения l получаем уравнение n -й степени:
.
Пусть это характеристическое уравнение имеет n различных корней 
. Тогда система дифференциальных уравнений имеет n решений:
1-е решение, соответствующее корню l = l 1:
; 
; …; 
;
2-е решение, соответствующее корню l = l 2:
; 
; …; 
;
……………………………………………………………………..
n -е решение, соответствующее корню l = ln:
; 
; …; 
.
Получена фундаментальная система решений. Общее решение системы имеет вид
Пример 1. Найти общее решение системы
Решение. Перепишем систему в виде
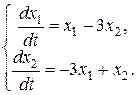
Рассмотрим характеристическое уравнение:
Подставим найдённые значения корней характеристического уравнения в систему линейных алгебраических уравнений относительно р 1, р 2.
Для 
имеем
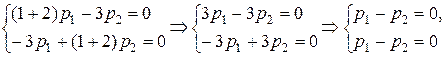
(второе уравнение есть следствие первого). Возьмём, например,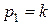 
; тогда 
. Полагая k = 1, найдем 
Итак, для 
получим 
Фундаментальная система решений:
для 
для
для 
Следовательно, общее решение системы имеет вид
Числовые ряды
Определение. Числовой ряд
(1)
называется сходящимся, если существует предел его частичных сумм 
. Число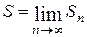 
называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимся.
|
|
|
Необходимый признак сходимости: если ряд (1) сходится, то его общий член стремится к нулю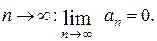 
К достаточным признакам сходимости рядов с положительными членами (аn ³ 0)относятся:
а) Признак сравнения в предельной форме: если
(2)
то ряды 
и 
одновременно сходятся или расходятся. В качестве эталонных рядов для сравнения обычно служат:
ряд 
, сходящийся при a >1 и расходящийся при a £ 1;
ряд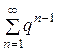 
, сходящийся при 0 £ q < 1 и расходящийся при q ³ 1.
Б) Признак Даламбера: если существует
(3)
то ряд сходится при 0 £ q <1 и расходится при q > 1. Если же q = 1, то вопрос о сходимости ряда этим признаком не решается.
Ряд с членами, имеющими разные знаки, называется условно сходящимся, если ряд сходится, а ряд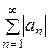 
расходится, и абсолютно сходящимся, если ряд 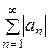сходится.
В) Признак Лейбница: если члены ряда удовлетворяют условиям: 1) 
(т.е. ряд знакочередующийся); 2) 
; 3) 
, то ряд сходится. Погрешность D, происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:
. (4)
Пример 1. Исследовать на сходимость числовой ряд
Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как общий член ряда 
, то, заменяя в выражении n -го члена n на n + 1, находим 
. Затем ищем предел отношения последующего члена аn +1 к предыдущему аn при n®¥:
Поскольку полученный предел равен единице, признак Даламбера не даёт ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем ряд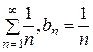 
и в силу формулы (2) получим
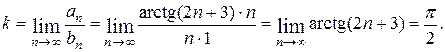
Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с общим членом bn = 1/ n расходится (гармоничный ряд).
Степенные ряды
Определение. Ряд вида
|
|
|
(1)
называется степенным рядом [относительно (х – а)], точка х = а – центром разложения, аn – коэффициентами ряда. Число R называется радиусом сходимости степенного ряда, если ряд (1) сходится при 
и расходится при 
. При 
ряд может, как сходится, так и расходится. Интервал 
называется интервалом сходимости степенного ряда (5). Радиус сходимости R может быть найден по формуле
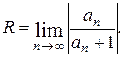(2)
Степенной ряд (1) внутри интервала сходимости можно почленно дифференцировать и интегрировать с сохранением радиуса сходимости.
3. Степенным рядом с комплексными членами называется выражение вида
,
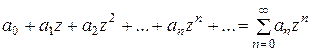где zn = xn + ijn, an – комплексные постоянные. Областью сходимости этого ряда является круг с центром в начале координат: 
, где R – радиус сходимости ряда.
По определению,
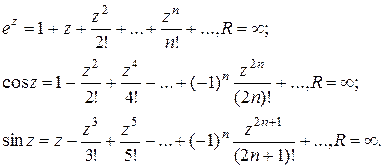(3)
Отсюда следует, что
(4)
Пример 1. Найти радиус и интервал сходимости степенного ряда 
. Исследовать сходимость ряда на концах интервала сходимости.
Решение. Радиус сходимости находим по формуле (6):
Интервал сходимости данного ряда определяется неравенства 
или 
.
Исследуем концы интервала сходимости. При х = –1 получаем числовой ряд
расходимость которого может быть установлена с помощью предельного признака сравнения (эталонный ряд – гармонический).
При х = –3 получаем числовой знакочередующийся ряд
который сходится по признаку Лейбница. Так как ряд, составленный из абсолютных членов данного ряда, т.е. ряд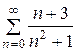 
, расходится, то исследуемый ряд сходится условно.
Таким образом, интервал сходимости исследуемого степенного ряда имеет вид 
.
Пример 2. Вычислить 
с точностью до 0,001.
Решение. Разложим подынтегральную функцию в биномиальный ряд по степеням х:
Так как отрезок интегрирования [–0,6; 0] находится внутри интервала сходимости биномиального ряда, то ряд можно почленно интегрировать. Подставляя в интеграл вышеприведенное разложение подынтегральной функции и почленно интегрируя в указанных пределах, получаем
Четвертый член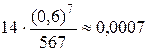 
меньше 0,001. Поэтому согласно неравенству (4) для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться первыми тремя членами ряда:
Ряды Фурье
Определение. Рядом Фурье периодической функции f (x), – l £ x £ l, называется ряд вида
|
|
|
Функция, заданная на полупериоде [0, l ], может быть представлена различными рядами Фурье. При чётном продолжении данной функции на второй полупериод [– l, 0) получается ряд по косинусам:
(1)
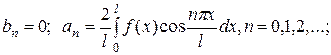
а при нечётном продолжении – ряд по синусам:
Пример 1. Разложить периодическую функцию 
, в ряд Фурье по косинусам. Построить график функции.
Решение. Данная функция определена на полупериоде [0, 3], т.е. l =3. Для разложения такой функции в ряд Фурье по косинусам ее следует продолжить на второй полупериод [–3, 0) чётным образом (рисунок 1). Для чётной функции коэффициенты bn = 0, а коэффициенты аn вычисляются по формулам:
 |
то отрезок интегрирования разобьем на два отрезка: от 0 до 1, где 
, и от 1 до 3, где 
. Тогда
При n = 0 имеем
Для вычисления коэффициентов an (n = 1, 2,…) применим метод интегрирования по частям:
причём в первом интеграле примем u = 1 – x, 
, откуда 
, 
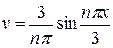. Во втором интеграле положим 
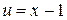, , откуда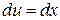 
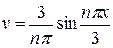, . Тогда
так как 
Следовательно, искомое разложение функции в ряд Фурье по косинусам имеет вид
.
Это разложение справедливо в области непрерывности данной функции.
|
|
|
