 |
Дифференциальные уравнения
|
|
|
|
1. Определение. Общим решением дифференциального уравнения первого порядка называется дифференцируемая функция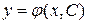 
, которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения 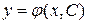при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям 
при 
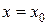(другая запись 
), называется задачей Коши.
Определение. График всякого решения 
данного дифференциального уравнения, построенный на плоскости хОу, называется интегральной кривой этого уравнения.
2. Определение. Уравнение вида 
называется линейным. Если 
, то уравнение называется однородным; если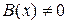 
– неоднородным.
Общее решение однородного уравнения получается путем разделения переменных; общее решение неоднородного уравнения получается из общего решения соответствующего однородного уравнения с помощью вариации произвольной постоянной интегрирования С.
Данное неоднородное уравнение можно интегрировать также с помощью замены 
, где u, v – две неизвестные функции.
3. Определение. Дифференциальное уравнение n-го порядка, разрешенное относительно производной, имеет вид 
.
Определение. Задача нахождения решения данного уравнения, удовлетворяющего начальным условиям
; 
; …; 
,
называется задачей Коши.
Для нахождения частного решения иногда используют так называемые краевые условия. Эти условия (их число не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Краевые условия ставятся лишь для уравнений порядка выше первого.
4. Теорема существования и единственности решения задачи Коши. Если в уравнении функция 
: а) непрерывна по всем своим аргументам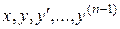 
в некоторой области D их изменения; б) имеет ограниченные в области D частные производные 
по аргументам 
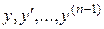, то найдется интервал 
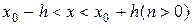, на котором существует единственное решение данного уравнения, удовлетворяющее условиям 
; 
; …; 
, где значения ; ;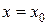 
; …; 
содержится в области D.
|
|
|
Проинтегрировать (в конечном виде) уравнение n -го порядка можно только в некоторых частных случаях.
5. Определение. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид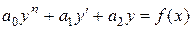 
, где а 0, а 1, а 2 – числа, причём 
. Если f (x) = 0, то уравнение называется однородным, а если 
– неоднородным.
6. Определение. Квадратное уравнение 
называется характеристическим уравнением дифференциального уравнения 
. Пусть 
– дискриминант квадратного уравнения. Возможны следующие случаи:
1) 
– общим решением уравнения является функция 
(k 1 и k 2 – корни характеристического уравнения);
2) 
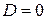– общим решением служит функция 
(k – корень характеристического уравнения);
3) 
– общим решением служит функция 
(k 1 = a + bi, k 2 = a – bi – корни характеристического уравнения).
7. Решение линейного неоднократного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.
Теорема. Если y * – некоторое частное решение неоднократного уравнения 
и Y – общее решение соответствующего однородного уравнения , то общее решение неоднородного уравнения имеет вид 
.
Укажем правило нахождения частного решения неоднородного уравнения методом неопределённых коэффициентов.
1) Пусть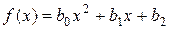 
; тогда:
а) 
, если нуль не является корнем характеристического уравнения;
б) 
, если нуль является простым корнем характеристического уравнения;
в)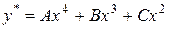 
, если нуль является двукратным корнем характеристического уравнения.
2) Пусть 
; тогда:
а) 
, если число a не является корнем характеристического уравнения;
|
|
|
б) 
, если число a является корнем характеристического уравнения;
в) 
, если число a является двукратным корнем характеристического уравнения.
3) Пусть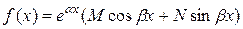 
; тогда:
а)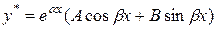 
, если число 
не является корнем характеристического уравнения;
б) 
, если число является корнем характеристического уравнения.
Пример 1. Найти общее решение уравнения 
и частное решение, удовлетворяющее начальному условию у (1) = 2.
Решение. Перепишем данное уравнение в виде: 
– и рассмотрим однородное уравнение 
. Так как 
(значение х = 0 не является решением неоднородного уравнения), то 
– общее решение однородного уравнения.
Применяем далее метод вариации произвольной С. Общее решение неоднородного уравнения будем искать в виде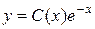 
; 
. Поставив значения y и 
в неоднородное уравнение, получим
Так как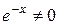 
, то
Подставив это значение С (х) в общее решение неоднородного уравнения, получим 
– общее решение неоднородного уравнения.
Для нахождения частного решения подставим значения х = 1, у = 2 в общее решение: 
. Значит, 
– частное решение неоднородного уравнения.
Пример 2. Найти общее решение уравнения 
и частное решение, удовлетворяющее начальным условиям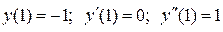 
.
Решение. Пусть 
. Имеем 
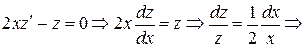
. Но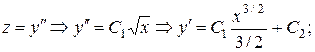 
.
Следовательно,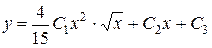 
– общее решение дифференциального уравнения.
Чтобы найти частное решение, подставим в выражения для у, и 
значение х = 1.
Из системы уравнений 
находим 
. Значит, искомое частное решение имеет вид
Пример 3. Найти общее решение уравнения 
и частное решение, удовлетворяющее начальным условиям 
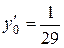при х = 0.
Решение. Рассмотрим однородное уравнение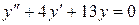 
. Соответствующее характеристическое уравнение имеет вид 
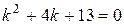, откуда 
, 
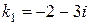. Следовательно, 
общее решение однородного уравнения.
Частное решение неоднородного уравнения будем искать в виде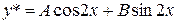 
. Имеем
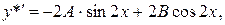
Подставим эти выражения в неоднородное уравнение
и получим систему для вычисления коэффициентов А и В:
Итак, частное решение неоднородного уравнения имеет вид
а общее решение неоднородного уравнения – вид
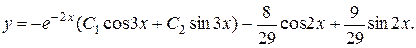
Найдём частное решение, удовлетворяющее заданным начальным условиям:
;
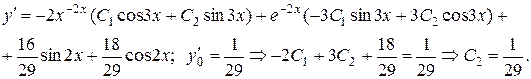
Искомое частное решение таково:
|
|
|
