 |
Циркуляция вектора индукции магнитного поля
|
|
|
|
Циркуляцией вектора индукции магнитного поля (циркуляцией вектора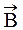 
) называют криволинейный интеграл по произвольному контуру L скалярного произведения вектора индукции 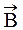и вектора элемента этого контура 
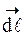, т. е.
, (25)
где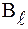 
- проекция 
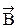на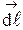 
.
6.1. Теорема о циркуляции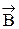 
Циркуляция 
по произвольному контуру L в вакууме равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охваченных этим контуром.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта, а ток противоположного направления - отрицательным (рис. 7, где I1 > 0, I3 > 0, I2 < 0, I4 < 0).
Рис.7.
|
Рассмотрим магнитное поле прямого проводника с током бесконечной длины (рис.8, ток направлен к нам). В качестве замкнутой поверхности используем окружность L радиуса r. Вектор индукции магнитного поля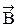 
перпендикулярен радиус-вектору 
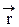и совпадает по направлению с вектором элемента длины 
.
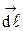Рис. 8
|
Согласно определению циркуляции вектора 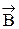имеем
, (cosa =1).
Применив формулу индукции прямого проводника с током бесконечной длины, последнее равенство перепишем в виде
. (26)
Теорема остается справедливой и для контура произвольной формы, который охватывает N проводников с током, т. е.
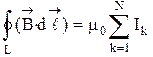. (27)
Формулу (27) называют законом полного тока.
Если ток распределен по объему, где расположен контур L, то
.
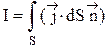Интеграл берется по произвольной поверхности S, натянутой на контур L.
Поэтому плотность тока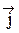 
под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали 
связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде
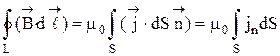. (28)
Замечание 1: Магнитное поле называют вихревым, или соленоидальным, поскольку циркуляция вектора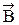 
не равна нулю (в отличие от электростатического поля, которое является потенциальным).
|
|
|
Замечание 2: Поле вектора 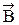определяется всеми токами, а циркуляция вектора 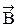- только теми токами, которые охватывает данный контур.
6.2. Дифференциальная форма теоремы о циркуляции 
Рассмотрим отношение циркуляции вектора к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали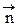 
к плоскости контура правилом правого винта. В пределе при S ® 0, имеем
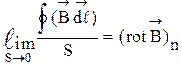. (29)
Формулу (29) называют ротором поля .
Следовательно, этот предел представляет собой скалярную величину, равную проекции вектора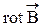 
на нормаль. Используя (29), формулу (28) представим в виде
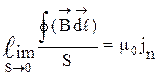(30)
или
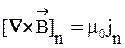, (31)
где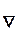 
- векторный дифференциальный оператор.
Следовательно,
. (32)
Ротор поля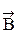 
совпадает по направлению с вектором плотности тока 
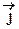в данной точке. Формула (32) - дифференциальная форма теоремы о циркуляции 
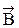. Дифференциальная форма теоремы о циркуляции 
расширяет ее возможности для исследования и расчета сложных магнитных полей.
7. Применение теоремы о циркуляции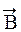 
Магнитное поле соленоида
Соленоидом называют катушку с током, витки которой намотаны вплотную друг к другу на цилиндрический каркас (рис. 9). Если длина соленоида много больше его диаметра, то магнитное поле снаружи его практически равно нулю. Магнитное поле внутри соленоида можно считать однородным.
Силовые линии магнитного поля направлены вдоль оси, причем вектор 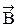составляет с направлением тока в соленоиде правовинтовую систему.
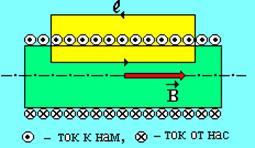Рис. 9
|
Найдем индукцию магнитного поля соленоида в центре на его оси, используя теорему о циркуляции .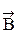
Пусть прямоугольный контур охватывает n витков (n - число витков на единицу длины соленоида, т. е. n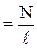 
, где N - полное число витков соленоида; 
- длина соленоида, витки с током которого охвачены прямоугольным контуром).
|
|
|
Циркуляция вектора по данному контуру 
.
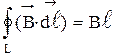Контур охватывает суммарный ток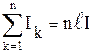 
.
Согласно теореме о циркуляции 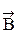, имеем В = m0n I.
Следовательно, индукция магнитного поля внутри соленоида
В = m0nI, (33)
где nI - число ампервитков.
|
|
|
