 |
Формулы численного дифференцирования.
|
|
|
|
Рассмотрим 1-ую формулу Ньютона И.М.:
дифференцируем по х:
Формулу в (5.1) дифференцируем по у:
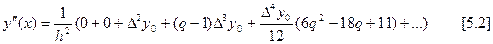
В формулах (5.1) и (5.2) решение можно обрывать раньше. При этом, если в этих формулах до k, то мы получим производную И.М., которая интерполирует функцию не во всех (
), а только (
) точках.
Пусть в (5.1) и (5.2)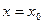 
, т.е. q=0, получаем:
(5.3) 
(5.4) 
На практике удобнее дифференцировать не односторонние формулы (1,2 формулы Ньютона), а центральные (формулу Стирлинга), так как узлы интерполяции располагаются симметрично относительно начальной точки x0. Возьмём в формуле Стирлинга первые три слагаемых (интерполяция по трём точкам x-1,x0,x1), получим:
Если же в формуле Стирлинга взять не 3, а 5 первых слагаемых (интерполяция по 5-ти точкам x-2,x-1,x0,x1,x2) продифференцируем и подставим 
, то получим:
Если взять 3 первых слагаемых и продифференцировать дважды по q, то получим:
Оценка погрешностей численного дифференцирования.
Также как и при интерполяции в численном дифференцировании возникают две погрешности: 
и 
.
Погрешность усечения – из-за замены функции на ее интерполирующий многочлен и ее производной на производную от интерполяционного многочлена.
Погрешность округления – из-за того, что значение функции в узлах xi известны не точно, а с некоторой погрешностью h. Оценим погрешность усечения.
Теорема 5.1:
Погрешность усечения в формуле (5.3) численного дифференцирования (при суммировании k-слагаемых) имеет следующую оценку:
где С Î [х0,хк].
Доказательство:
Замечания:
При доказательстве теоремы был использован тот факт, что С=С(х) и С’(x) – существует. Это будет так, если функция f была достаточно гладкой.
Из-за того, что С’(x) мы вообще никак не можем оценить, погрешность усечения мы можем находить только в узлах интерполяции, с тем, чтобы 1-ое слагаемое, где присутствует С’(x), занулилось.
|
|
|
На практике формулу (5.8) мы заменяем на формулу (5.9) (оценка сверху для )
(5.9)
где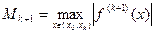 
Вспомним, что конечная разность очень похожа на производную (
).
Тогда (5.9) можно заменить на (5.10):
Для формул (5.5), (5.6) и (5.7) можно вывести таким же образом, как и в теореме 5.1, получаем:
Для (5.5) ® 
Для (5.6) ® 
Для (5.7) → 
где 
, 
Оценим для центральных формул.
Рассмотрим формулу (5.5)
, 
таким образом : 
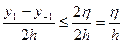
Аналогично:
для (5.6) ® 
для (5.7) ® 
Заметим, что во всех формулах при 
и при 
Поэтому имеем следующую картину:
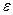
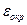
Таблица для погрешностей центральных формул:
| 
|
| 
| |
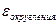
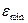
| 4.6 | 
| 
| 
| 
|
| 4.7 | 
| 
| 
| 15/8 
|
| 4.8 | 
| 
| 
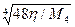
| 2/ 
|
П.6. Численное интегрирование.
Общая идея, решение.
Постановка задачи: в узлах 
заданы значения функции 
= f() 
Необходимо найти значение 
для любых a,b.
Основная идея численного интегрирования: заменить функцию f(x) на интерполирующую ее функцию, которую мы и будем интегрировать.
, где 
не зависит от исходной функции f, а зависит от узлов интерполяции .
Вычислим :
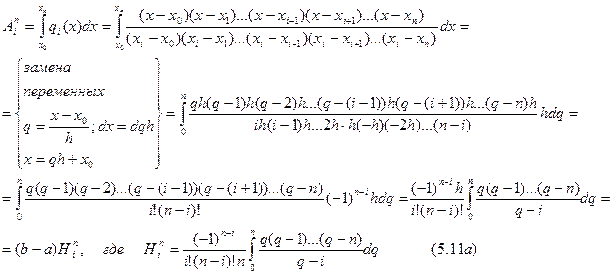
Замечания:
Замена 
на 
была сделана с той целью, чтобы коэффициенты Ч.И. не зависели от h, а зависели от n и i.
Частные случаи, формулы Ньютона - Котеса.
Итак, формула Ч.И. принимает следующий вид:
(5.11б)
где 
вычисляется по формуле (5.11а).
Выпишем частные случаи (5.11а):
n=1
Таким образом, при n=1, формула Ньютона - Котеса следующий вид:
(5.12) – формула трапеций Ч.И. (выражение из правой части площадь трапеции):
Вычислим коэффициенты Н.-К. n=2:
Итак, при n=2, формула Ч.И. принимает следующий вид (формула Симпсона):
Аналогичным образом вычисляем коэффициенты при большем n.
Таблица коэффициентов Ньютона - Котеса:
| i n | ||||||||
| H0 | ½ | 1/6 | 1/8 | 7/90 | 19/288 | 41/840 | 751/17280 | 989/28350 |
| H1 | ½ | 2/3 | 3/8 | 32/90 | 75/288 | 216/840 | 3577/17280 | 5888/28350 |
| H2 | 1/6 | 3/8 | 12/90 | 60/288 | 27/840 | 1323/17280 | -928/28350 | |
| H3 | 1/8 | 32/90 | 50/288 | 272/840 | 2989/17280 | 10496/28350 | ||
| H4 | 7/90 | 75/288 | 27/840 | 2989/17280 | */28350 | |||
| H5 | 19/288 | 216/840 | 1323/17280 | 10496/28350 | ||||
| H6 | 41/840 | 3577/17280 | -928/28350 | |||||
| H7 | 751/17280 | *5888/28350 | ||||||
| H8 | 989/28350 |
|
|
|
|
|
|
