 |
Факторный анализ. Метод главных компонент
|
|
|
|
В стремлении предельно точно описать исследуемую область аналитики часто отбирают большое число независимых переменных (p). В этом случае может возникнуть серьезная ошибка: несколько описывающих переменных могут характеризовать одну и ту же сторону зависимой переменной и, как следствие, высоко коррелировать между собой. Мультиколлинеарность независимых переменных серьезно искажает результаты исследования, поэтому от нее следует избавляться.
Метод главных компонент (как упрощенная модель факторного анализа, поскольку при этом методе не используются индивидуальные факторы, описывающие только одну переменную xi) позволяет объединить влияние высоко коррелированных переменных в один фактор, характеризующий зависимую переменную с одной единственной стороны. В результате анализа, осуществленного по методу главных компонент, мы добьемся сжатия информации до необходимых размеров, описания зависимой переменной m (m<p) числом обобщенных факторов, линейно зависящих от исходных признаков, а также выявления взаимосвязи наблюдаемых признаков с полученными факторами. Далее мы построим уравнение регрессии на главных компонентах и сравним результаты с построенными ранее уравнениями регрессии. Достоинством главных компонент, полученных в результате анализа, является их некоррелируемость между собой.
Для начала необходимо решить, сколько факторов необходимо выделить в данном исследовании. В рамках метода главных компонент первый главный фактор описывает наибольших процент дисперсии независимых переменных, далее – по убывающей. Таким образом, каждая следующая главная компонента, выделенная последовательно, объясняет все меньшую долю изменчивости факторов xi. Задача исследователя состоит в том, чтобы определить, когда изменчивость становится действительно малой и случайной. Другими словами – сколько главных компонент необходимо выбрать для дальнейшего анализа.
|
|
|
Существует несколько методов рационального выделения необходимого числа факторов. Наиболее используемый из них – критерий Кайзера. Согласно этому критерию, отбираются только те факторы, собственные значения которых больше 1. Таким образом, фактор, который не объясняет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, опускается.
Проанализируем Таблицу 19, построенную в SPSS:
Таблица 19. Полная объясненная дисперсия
| Компонента | Начальные собственные значения | Суммы квадратов нагрузок вращения | ||||||
| Итого | % Дисперсии | Кумулятивный % | Итого | % Дисперсии | Кумулятивный % | |||
| dimension0 | 5,442 | 90,700 | 90,700 | 3,315 | 55,246 | 55,246 | ||
| ,457 | 7,616 | 98,316 | 2,304 | 38,396 | 93,641 | |||
| ,082 | 1,372 | 99,688 | ,360 | 6,005 | 99,646 | |||
| ,009 | ,153 | 99,841 | ,011 | ,176 | 99,823 | |||
| ,007 | ,115 | 99,956 | ,006 | ,107 | 99,930 | |||
| ,003 | ,044 | 100,000 | ,004 | ,070 | 100,000 | |||
| Метод выделения: Анализ главных компонент. |
Как видно из Таблицы 19, в данном исследовании переменные xi высоко коррелирут между собой (это также выявлено ранее и видно из Таблицы 5 «Парные коэффициенты корреляции»), а следовательно, характеризуют зависимую переменную Y практически с одной стороны: изначально первая главная компонента объясняет 90,7 % дисперсии xi, и только собственное значение, соответствующее первой главной компоненте, больше 1. Конечно, это является недостатком отбора данных, однако в процессе самого отбора этот недостаток не был очевиден.
Анализ в пакете SPSS позволяет самостоятельно выбрать число главных компонент. Выберем число 6 – равное количеству независимых переменных. Второй столбец Таблицы 19 показывает суммы квадратов нагрузок вращения, именно по этим результатам и сделаем вывод о числе факторов. Собственные значения, соответствующие первым двум главным компонентам, больше 1 (55,246% и 38,396% соответственно), поэтому, согласно методу Кайзера, выделим 2 наиболее значимые главные компоненты.
|
|
|
Второй метод выделения необходимого числа факторов – критерий «каменистой осыпи». Согласно этому методу, собственные значения представляются в виде простого графика, и выбирается такое место на графике, где убывание собственных значений слева направо максимально замедляется:
Рисунок 3. Критерий "каменистой осыпи"

Как видно на Рисунке 3, убывание собственных значений замедляется уже со второй компоненты, однако постоянная скорость убывания (очень маленькая) начинается лишь с третьей компоненты. Следовательно, для дальнейшего анализа будут отобраны первые две главные компоненты. Это умозаключение согласуется с выводом, полученным при использовании метода Кайзера. Таким образом, окончательно выбираются первые две последовательно полученные главные компоненты.
После выделения главных компонент, которые будут использоваться в дальнейшем анализе, необходимо определить корреляцию исходных переменных xi c полученными факторами и, исходя из этого, дать названия компонентам. Для анализа воспользуемся матрицей факторных нагрузок А, элементы которой являются коэффициентами корреляции факторов с исходными независимыми переменными:
Таблица 20. Матрица факторных нагрузок
| Матрица компонентa | ||||||
| Компонента | ||||||
| X1 | ,956 | -,273 | ,084 | ,037 | -,049 | ,015 |
| X2 | ,986 | -,138 | ,035 | -,080 | ,006 | ,013 |
| X3 | ,963 | -,260 | ,034 | ,031 | ,060 | -,010 |
| X4 | ,977 | ,203 | ,052 | -,009 | -,023 | -,040 |
| X5 | ,966 | ,016 | -,258 | ,008 | -,008 | ,002 |
| X6 | ,861 | ,504 | ,060 | ,018 | ,016 | ,023 |
| Метод выделения: Анализ методом главных компонент. | ||||||
| a. Извлеченных компонент: 6 |
В данном случае интерпретация коэффициентов корреляции затруднена, следовательно, довольно сложно дать названия первым двум главным компонентам. Поэтому далее воспользуемся методом ортогонального поворота системы координат Варимакс, целью которого является поворот факторов так, чтобы выбрать простейшую для интерпретации факторную структуру:
|
|
|
Таблица 21. Коэффициенты интерпретации
| Матрица повернутых компонентa | ||||||
| Компонента | ||||||
| X1 | ,911 | ,384 | ,137 | -,021 | ,055 | ,015 |
| X2 | ,841 | ,498 | ,190 | ,097 | ,000 | ,007 |
| X3 | ,900 | ,390 | ,183 | -,016 | -,058 | -,002 |
| X4 | ,622 | ,761 | ,174 | ,022 | ,009 | ,060 |
| X5 | ,678 | ,564 | ,472 | ,007 | ,001 | ,005 |
| X6 | ,348 | ,927 | ,139 | ,001 | -,004 | -,016 |
| Метод выделения: Анализ методом главных компонент. Метод вращения: Варимакс с нормализацией Кайзера. | ||||||
| a. Вращение сошлось за 4 итераций. |
Из Таблицы 21 видно, что первая главная компонента больше всего связана с переменными x1, x2, x3; а вторая – с переменными x4, x5, x6. Таким образом, можно сделать вывод, что объем инвестиций в основные средства в регионе (переменная Y) зависит от двух факторов:
- объема собственных и заемных средств, поступивших в предприятия региона за период (первая компонента, z1);
- а также от интенсивности вложений предприятий региона в финансовые активы и количества иностранного капитала в регионе (вторая компонента, z2).
Далее построим диаграмму рассеивания по первым двум главным компонентам:
Рисунок 4. Диаграмма рассеивания

Данная диаграмма демонстрирует неутешительные результаты. Еще в самом начале исследования мы старались подобрать данные так, чтобы результирующая переменная Y была распределена нормально, и нам практически это удалось. Законы распределения независимых переменных были достаточно далеки от нормального, однако мы старались максимально приблизить их к нормальному закону (соответствующим образом подобрать данные). Рисунок 4 показывает, что первоначальная гипотеза о близости закона распределения независимых переменных к нормальному закону не подтверждается: форма облака должна напоминать эллипс, в центре объекты должны быть расположены более густо, нежели чем по краям. Стоит заметить, что сделать многомерную выборку, в которой все переменные распределены по нормальному закону – задача, выполнимая с огромным трудом (более того, не всегда имеющая решение). Однако к этой цели нужно стремиться: тогда результаты анализа будут более значимыми и понятными при интерпретации. К сожалению, в нашем случае, когда проделана большая часть работы по анализу собранных данных, менять выборку достаточно затруднительно. Но далее, в последующих работах, стоит более серьезно подходить в выборке независимых переменных и максимально приближать закон их распределения к нормальному.
|
|
|
Последним этапом анализа методом главных компонент является построение уравнения регрессии на главные компоненты (в данном случае – на первую и вторую главные компоненты).
При помощи SPSS рассчитаем параметры регрессионной модели:
Таблица 22. Параметры уравнения регресии на главные компоненты
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | |||
| B | Стд. Ошибка | Бета | |||||
| (Константа) | 47414,184 | 1354,505 | 35,005 | ,001 | |||
| Z1 | 26940,937 | 1366,763 | ,916 | 19,711 | ,001 | ||
| Z2 | 6267,159 | 1366,763 | ,213 | 4,585 | ,001 | ||
Уравнение регрессии примет вид:
y=47 414,184 + 0,916*z1+0,213*z2,
(b0) (b1) (b2)
т. о. b0 = 47 414,184 показывает точку пересечения прямой регрессии с осью результирующего показателя;
b1= 0,916 – при увеличении значения фактора z1 на 1 ожидаемое среднее значение суммы объема инвестиций в основные средства увеличится на 0,916;
b2= 0,213 – при увеличении значения фактора z2 на 1 ожидаемое среднее значение суммы объема инвестиций в основные средства увеличится на 0,213.
В данном случае значение tкр («альфа»=0,001, «ню»=53) = 3,46 меньше tнабл для всех коэффициентов «бета». Следовательно, все коэффициенты значимы.
Далее оценим качество построенной модели:
Таблица 24. Качество регрессионной модели на главные компоненты
| Модель | R | R-квадрат | Скорректированный R-квадрат | Стд. ошибка оценки | |||
| dimension0 | ,941a | ,885 | ,881 | 10136,18468 | |||
| a. Предикторы: (конст) Z1, Z2 | |||||||
| b. Зависимая переменная: Y | |||||||
В Таблице 24 отражены показатели, которые характеризуют качество построенной модели, а именно: R – множественный к-т корреляции – говорит о том, какая доля дисперсии Y объясняется вариацией Z; R^2 – к-т детерминации – показывает долю объяснённой дисперсии отклонений Y от её среднего значения. Стандартная ошибка оценки характеризует ошибку построенной модели. Сравним эти показатели с аналогичными показателями степенной регрессионной модели (ее качество оказалось выше качества линейной модели, поэтому сравниваем именно со степенной):
Таблица 25. Качество степенной регрессионной модели
| Модель | R | R-Квадрат | Скорректированный R-квадрат | Стд. ошибка оценки |
| (d) | ,991(d) | ,981 | ,980 | ,10909 |
Так, множественный к-т корреляции R и к-т детерминации R^2 в степенной модели несколько выше, чем в модели главных компонент. Кроме того, стандартная ошибка модели главных компонент НАМНОГО выше, чем в степенной модели. Поэтому качество степенной регрессионной модели выше, чем регрессионной модели, построенной на главных компонентах.
|
|
|
Проведем верификацию регрессионной модели главных компонент, т. е. проанализируем ее значимость. Проверим гипотезу о незначимости модели, рассчитаем F(набл.) = 204,784 (рассчитано в SPSS), F(крит) (0,001; 2; 53)=7,76. F(набл)>F(крит), следовательно, гипотеза о незначимости модели отвергается. Модель значима.
Итак, в результате проведения компонентного анализа, было выяснено, что из отобранных независимых переменных xi можно выделить 2 главные компоненты – z1 и z2, причем на z1 в большей степени влияют переменные x1, x2, x3, а на z2 – x4, x5, x6. Уравнение регрессии, построенное на главных компонентах, оказалось значимым, хотя и уступает по качеству степенному уравнению регрессии. Согласно уравнению регрессии на главные компоненты, Y положительно зависит как от Z1, так и от Z2. Однако изначальная мультиколлинеарность переменных xi и то, что они не распределены по нормальному закону распределения, может искажать результаты построенной модели и делать ее менее значимой.
Кластерный анализ
Следующим этапом данного исследования является кластерный анализ. Задачей кластерного анализа является разбиение выбранных регионов (n=56) на сравнительно небольшое число групп (кластеров) на основе их естественной близости относительно значений переменных xi. При проведении кластерного анализа мы предполагаем, что геометрическая близость двух или нескольких точек в пространстве означает физическую близость соответствующих объектов, их однородность (в нашем случае - однородность регионов по показателям, влияющим на инвестиции в основные средства).
На первой стадии кластерного анализа необходимо определиться с оптимальным числом выделяемых кластеров. Для этого необходимо провести иерархическую кластеризацию – последовательное объединение объектов в кластеры до тех пор, пока не останется два больших кластера, объединяющиеся в один на максимальном расстоянии друг от друга. Результат иерархического анализа (вывод об оптимальном количестве кластеров) зависит от способа расчета расстояния между кластерами. Таким образом, протестируем различные методы и сделаем соответствующие выводы.
Метод «ближнего соседа»
Если расстояние между отдельными объектами мы рассчитываем единым способом – как простое евклидово расстояние – расстояние между кластерами вычисляется разными методами. Согласно методу «ближайшего соседа», расстояние между кластерами соответствует минимальному расстоянию между двумя объектами разных кластеров.
Анализ в пакете SPSS проходит следующим образом. Сначала рассчитывается матрица расстояний между всеми объектами, а затем, на основе матрицы расстояний, объекты последовательно объединяются в кластеры (для каждого шага матрица составляется заново). Шаги последовательного объединения представлены в таблице:
Таблица 26. Шаги агломерации. Метод «ближайшего соседа»
| Этап | Кластер объединен с | Коэффициенты | Этап первого появления кластера | Следующий этап | ||
| Кластер 1 | Кластер 2 | Кластер 1 | Кластер 2 | |||
| ,003 | ||||||
| ,004 | ||||||
| ,004 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,006 | ||||||
| ,007 | ||||||
| ,007 | ||||||
| ,009 | ||||||
| ,010 | ||||||
| ,010 | ||||||
| ,010 | ||||||
| ,010 | ||||||
| ,011 | ||||||
| ,012 | ||||||
| ,012 | ||||||
| ,012 | ||||||
| ,012 | ||||||
| ,012 | ||||||
| ,013 | ||||||
| ,014 | ||||||
| ,014 | ||||||
| ,014 | ||||||
| ,014 | ||||||
| ,015 | ||||||
| ,015 | ||||||
| ,016 | ||||||
| ,017 | ||||||
| ,018 | ||||||
| ,018 | ||||||
| ,019 | ||||||
| ,019 | ||||||
| ,020 | ||||||
| ,021 | ||||||
| ,021 | ||||||
| ,022 | ||||||
| ,024 | ||||||
| ,025 | ||||||
| ,027 | ||||||
| ,030 | ||||||
| ,033 | ||||||
| ,034 | ||||||
| ,042 | ||||||
| ,052 | ||||||
| ,074 | ||||||
| ,101 | ||||||
| ,103 | ||||||
| ,126 | ||||||
| ,163 | ||||||
| ,198 | ||||||
| ,208 | ||||||
| ,583 | ||||||
| 1,072 |
Как видно из Таблицы 26, на первом этапе объединились элементы 7 и 8, т. к. расстояние между ними было минимальным – 0,003. Далее расстояние между объединенными объектами увеличивается. По таблице также можно сделать вывод об оптимальном числе кластеров. Для этого нужно посмотреть, после какого шага происходит резкий скачок в величине расстояния, и вычесть номер этой агломерации из числа исследуемых объектов. В нашем случае: (56-53)=3 – оптимальное число кластеров.

Рисунок 5. Дендрограмма. Метод "ближайшего соседа"
Аналогичный вывод об оптимальном количестве кластеров можно сделать и глядя на дендрограмму (Рис. 5): следует выделить 3 кластера, причем в первый кластер войдут объекты под номерами 1-54 (всего 54 объекта), а во второй и третий кластеры – по одному объекту (под номерами 55 и 56 соответственно). Данный результат говорит о том, что первые 54 региона относительно однородны по показателям, влияющим на инвестиции в основные средства, в то время как объекты под номерами 55 (Республика Дагестан) и 56 (Новосибирская область) значительно выделяются на общем фоне. Стоит заметить, что данные субъекты имеют самые большие объемы инвестиций в основные средства среди всех отобранных регионов. Этот факт еще раз доказывает высокую зависимость результирующей переменной (объема инвестиций) от выбранных независимых переменных.
Аналогичные рассуждения проводятся для других методов расчета расстояния между кластерами.
Метод «дальнего соседа»
Таблица 27. Шаги агломерации. Метод "дальнего соседа"
| Этап | Кластер объединен с | Коэффициенты | Этап первого появления кластера | Следующий этап | ||
| Кластер 1 | Кластер 2 | Кластер 1 | Кластер 2 | |||
| ,003 | ||||||
| ,004 | ||||||
| ,004 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,005 | ||||||
| ,007 | ||||||
| ,009 | ||||||
| ,010 | ||||||
| ,010 | ||||||
| ,011 | ||||||
| ,011 | ||||||
| ,012 | ||||||
| ,012 | ||||||
| ,014 | ||||||
| ,014 | ||||||
| ,014 | ||||||
| ,017 | ||||||
| ,017 | ||||||
| ,018 | ||||||
| ,018 | ||||||
| ,019 | ||||||
| ,021 | ||||||
| ,022 | ||||||
| ,026 | ||||||
| ,026 | ||||||
| ,027 | ||||||
| ,034 | ||||||
| ,035 | ||||||
| ,035 | ||||||
| ,037 | ||||||
| ,037 | ||||||
| ,042 | ||||||
| ,044 | ||||||
| ,046 | ||||||
| ,063 | ||||||
| ,077 | ||||||
| ,082 | ||||||
| ,101 | ||||||
| ,105 | ||||||
| ,117 | ||||||
| ,126 | ||||||
| ,134 | ||||||
| ,142 | ||||||
| ,187 | ||||||
| ,265 | ||||||
| ,269 | ||||||
| ,275 | ||||||
| ,439 | ||||||
| ,504 | ||||||
| ,794 | ||||||
| ,902 | ||||||
| 1,673 | ||||||
| 2,449 |
При методе «дальнего соседа» расстояние между кластерами рассчитывается как максимальное расстояние между двумя объектами в двух разных кластерах. Согласно Таблице 27, оптимальное число кластеров равно (56-53)=3.
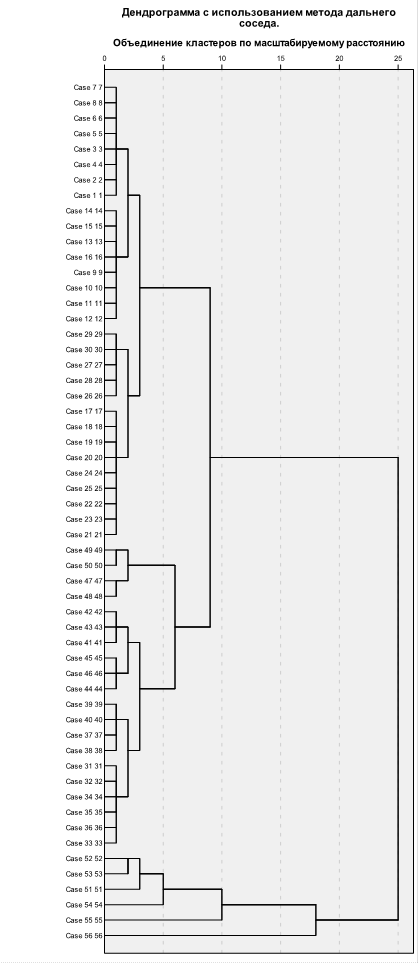
Рисунок 6. Дендрограмма. Метод "дальнего соседа"
Согласно дендрограмме, оптимальным решением также будет выделение 3 кластеров: в первый кластер войдут регионы под номерами 1-50 (50 регионов), во второй – под номерами 51-55 (5 регионов), в третий – последний регион под номером 56.
Метод «центра тяжести»
При методе «центра тяжести» за расстояние между кластерами принимается евклидово расстояние между «центрами тяжести» кластеров – средними арифметическими их показателей xi.
При анализе таблицы шагов объединения (далее не будем приводить саму таблицу из-за ее громоздкости) выяснилось, что оптимальное количество кластеров равно (56-52)=4.
Далее рассмотрим дендрограмму:

Рисунок 7. Дендрограмма. Метод "центра тяжести"
На Рисунке 7 видно, что оптимальное число кластеров следующее: 1 кластер – 1-47 объекты; 2 кластер – 48-54 объекты (всего 6); 3 кластер – 55 объект; 4 кластер – 56 объект.
Принцип «средней связи»
В данном случае расстояние между кластерами равно среднему значению расстояний между всеми возможными парами наблюдений, причем одно наблюдение берется из одного кластера, а второе – соответственно, из другого.
Анализ таблицы шагов агломерации показал, что оптимальное количество кластеров равно (56-52)=4. Сравним этот вывод с выводом, полученным при анализе дендрограммы. На Рисунке 8 видно, что в 1 кластер войдут объекты под номерами 1-50, во 2 кластер – объекты 51-54 (4 объекта), в 3 кластер – 55 регион, в 4 кластер – 56 регион.
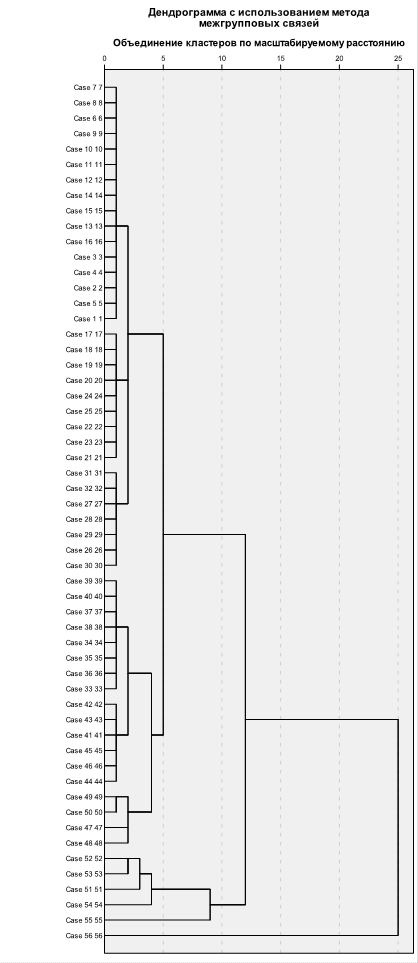
Рисунок 8. Дендрограмма. Метод "средней связи"
|
|
|


