 |
Метод «средней связи элементов разных кластеров и внутри групп»
|
|
|
|
В данном методе расстояние между кластерами рассчитывается на основании всех возможных пар наблюдений, принадлежащих обоим кластерам, причем учитываются также пары наблюдений, образующиеся внутри кластеров. В этом случае получаются интересные результаты. Оптимальное число кластеров равно 4: в первый кластер войдут 34 региона, во второй – 18 регионов, в третий – 3 региона (под номерами 52-54), а в 4 – один регион под номером 56.

Рисунок 9. Дендрограмма №5
На основании иерархического кластерного анализа, проведенного различными методами, можно сделать вывод, что оптимальное число кластеров равно 4.
Метод k-средних
Несмотря достоинства иерархического метода (можно отследить поэтапное объединение объектов в кластеры), при большом количестве объектов проводить данный анализ весьма сложно. Поэтому в случае, когда число объектов n велико, применяют метод k-средних. Идея этого метода состоит в том, чтобы разбить анализируемое множество объектов n на заранее известное число кластеров k, причем данное разбиение должно минимизировать функционал качества – сумму внутриклассовых дисперсий:
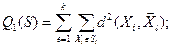
При помощи пакета SPSS рассчитаем значения средних показателей в кластерах:
Таблица 28. Конечные центры кластеров
| Кластер | ||||
| X1 | ||||
| X2 | ||||
| X3 | ||||
| X4 | ||||
| X5 | ||||
| X6 |
На основании Рисунка 10 можно сделать вывод, что 1 кластер характеризуется самыми низкими средними значениями показателей xi, в то время как 4 кластер – самыми высокими средними значениями соответствующих показателей. Таким образом, чем выше номер кластера, тем выше средние значения показателей xi.
|
|
|
Рисунок 10. Средние значения показателей в кластерах

В следующей таблице представлены регионы, входящие в каждый кластер:
Таблица 29. Распределение регионов по кластерам
| 1 кластер (32 региона) | 2 кластер (19 регионов) | 3 кластер (4 региона) | 4 кластер (1 регион) |
| Чукотский авт. округ | Смоленская область | Оренбургская область | Республика Дагестан |
| Республика Тыва | Владимирская область | Иркутская область | |
| Республика Калмыкия | Тамбовская область | Республика Коми | |
| Республика Алтай | Калининградская область | Новосибирская область | |
| Республика Адыгея | Алтайский край | ||
| Костромская область | Астраханская область | ||
| Магаданская область | Вологодская область | ||
| Респ. Северная Осетия | Ярославская область | ||
| Кабардино-Балкарская респ. | Тульская область | ||
| Псковская область | Омская область | ||
| Еврейская авт. область | Калужская область | ||
| Республика Хакасия | Волгоградская область | ||
| Орловская область | Томская область | ||
| Республика Марий Эл | Саратовская область | ||
| Республика Карелия | Архангельская область | ||
| Курганская область | Амурская область | ||
| Ивановская область | Тверская область | ||
| Камчатский край | Белгородская область | ||
| Республика Бурятия | Липецкая область | ||
| Кировская область | |||
| Мурманская область | |||
| Рязанская область | |||
| Республика Мордовия | |||
| Ненецкий авт. Округ | |||
| Новгородская область | |||
| Брянская область | |||
| Забайкальский край | |||
| Удмуртская республика | |||
| Чувашская республика | |||
| Курская область | |||
| Ульяновская область | |||
| Пензенская область |
|
|
|
Регионы, входящие в состав 1 кластера, характеризуются самыми низкими средними значениями всех показателей xi, и далее чем выше номер кластера – тем выше средние значения соответствующие значения показателей. Интересно, что аналогичная картина вырисовывается и при распределении данных регионов по среднему уровню инвестиций в основные средства: чем выше номер кластера, тем выше средний уровень инвестиций в основные средства (результирующий показатель Y):
Таблица 30. Среднее значение объема инвестиций в основные средства (переменная Y)
| 1 кластер (32 региона) | 2 кластер (19 регионов) | 3 кластер (4 региона) | 4 кластер (1 регион) |
Таким образом, деление регионов на кластеры, однородные по средним значениям независимых переменных, соответствует группировке этих регионов по среднему значению результирующей переменной. Следовательно, объем инвестиций в основные средства действительно тесно зависит от переменных xi.
Важной целью кластерного анализа является минимизация расстояния между объектами, находящимися в пределах одного кластера, и максимизация расстояния между кластерами. В этой связи рассмотрим следующую таблицу:
Таблица 31. Межгрупповая дисперсия
| Кластер | |||||
Из Таблицы 31 видно, что расстояние между кластерами очень велико, причем расстояние между 1 и 2 кластером намного меньше, чем расстояние, скажем, между 1 и 3 и тем более 1 и 4 кластерами. Учитывая предыдущие размышления о характере объектов, попавших в каждый кластер (об средних значениях показателей xi), этот результат представляется весьма логичным.
Поскольку анализ проводился на основании 6 независимых переменных, наглядно представить его результаты при помощи графиков – достаточно сложная задача. Скорее всего, на многомерном графике сложилась бы следующая картина: объекты, находящиеся в одном кластере, образовали бы «облако» точек, элементы которого находятся на достаточно близком расстоянии друг от друга. Вместе с тем, отдельные «облака» находились бы на большом друг от друга расстоянии. По крайней мере, такая «картинка» представляется автору работы крайне желательной.
|
|
|
Итак, в результате кластерного анализа были выделены 4 кластера и охарактеризованы особенности такой классификации. Далее перейдем к дискриминантному.
Дискриминантный анализ
Последней стадией данного исследования является проведение дискриминантного анализа. Плюсом этого анализа является то, что он позволяет проверить результаты проведенной ранее кластеризации наблюдений.
При помощи дискриминантного анализа в пакете SPSS проверим результаты кластерного анализа. В результате получим, что практически все наблюдения были классифицированы корректно: результаты распределения по группам совпали с результатами кластерного анализа, вероятности попадания в нужный кластер близки к 1, вероятности попадания в другие кластеры близка к 0. Смоленская область – единственный регион, классифицированный ошибочно:
Таблица 32. Поверка кластерного анализа
| Кластерный анализ | Регион | Дискриминантный анализ | Апостериорная в-ть (1) | Апостериорная в-ть (2) | Апостериорная в-ть (3) | Апостериорная в-ть (4) |
| … | … | … | … | … | … | … |
| Пензенская обл. | 0,9874 | 0,0126 | 0,0000 | |||
| Смоленская обл. | 0,5047 | 0,4953 | 0,0000 | |||
| Владимирская обл. | 0,3326 | 0,6674 | 0,0000 | |||
| … | … | … | … | … | … | … |
Согласно кластерному анализу Смоленская область должна была войти во 2 кластер, однако апостериорная вероятность попадания этого региона в 1 кластер является самой высокой, следовательно, Смоленская область должна быть отнесена к 1 кластеру.
Далее перейдем к построению дискриминантной функции. По значению этой функции мы можем определить, к какому кластеру лучше всего отнести новое, ранее не классифицированное наблюдение. Поскольку классификация проходит по числу групп m>2 (m=4), было получено несколько вариантов дискриминантной функции, а именно – 3. Средние значения дискриминантных функций составили:
Таблица 33. Средние значения дискриминантных функций
| Функции в центроидах групп | ||||
| Кластерный номер наблюдения | Функция | |||
| dimension0 | 2,990 | -2,176 | ,499 | |
| 4,634 | 11,183 | 1,398 | ||
| 3,170 | 1,288 | -1,136 | ||
| -174,440 | ,439 | ,030 | ||
Важным показателем качества дискриминантной функции является коэффициент канонической корреляции – мера связи между четырьмя (в данном случае) множествами переменных. Чем выше его величина, тем выше разделительная способность дискриминантной функции (максимальное значение равно единице). Сравним коэффициенты канонической корреляции трех полученных дискриминантных функций:
|
|
|
Таблица 34. Качество дискриминантных функций
| Функция | Собственное значение | % объясненной дисперсии | Кумулятивный % | Каноническая корреляция | |
| dimension0 | 596,002a | 97,7 | 97,7 | ,999 | |
| 13,144a | 2,2 | 99,9 | ,964 | ||
| ,775a | ,1 | 100,0 | ,661 | ||
Как видно из Таблицы 34, первая дискриминантная функция характеризуется самым высоким значением коэффициента канонической корреляции – 0,999. Кроме того, степень разделения кластеров зависит от собственного значения дискриминантной функции: чем больше собственное значение, тем выше степень разделения. Первая функция имеет наибольшее собственное значение (далее – вторая и т. д.), а значит, обладает наибольшей разделительной способностью. Также из Таблицы 34 видно, что первая функция объясняет наибольшую долю дисперсии признаков. Таким образом, приведенные выше рассуждения доказывают, что первая дискриминантная функция – лучший инструмент для проверки принадлежности нового наблюдения к той или иной обучающей выборке.
Чтобы проверить, значимо ли отличаются средние значения дискриминантной функции в четырех выделенных кластерах, используют Лябду-Уилкса:
Таблица 35. Лямбда-Уилкса
| Проверка функции(й) | Лямбда Уилкса | Хи-квадрат | ст.св. | Знч. | |
| dimension0 | ,000 | 480,747 | ,000 | ||
| ,040 | 161,151 | ,000 | |||
| ,563 | 28,687 | ,000 |
Согласно Таблице 35, средние значения первой дискриминантной функции в четырех различных кластерах очень значимо различаются (лямбда очень мала).
Далее проверим значимость первой дискриминантной функции. Тест на значимость проводится при помощи лямбда-статистики Уилкса. Чем меньше эта статистика, тем более значимой является дискриминантная функция. Смысл теста заключается в следующем. Критерий лямбда-статистики Уилкса оценивает остаточную дискриминантную способность, т. е. способность функции различать кластеры, при условии, что информация, полученная с помощью ранее рассчитанных выборок, отсутствует. Логично, что, если остаточная дискриминантная способность мала, нет никакого смысла выводить следующую дискриминантную функцию. В Таблице 35 мы видим, что первая функция обладает самым низким значением лямбды. Следовательно, она (первая функция) является наиболее значимой.
|
|
|
Далее рассмотрим структурную матрицу:
Таблица 36. Структурная матрица
| Функция | |||
| X4 | -,176 | ,807 | -,293 |
| X1 | -,058 | ,724 | -,325 |
| X6 | -,344 | ,663 | -,131 |
| X2 | -,072 | ,634 | -,425 |
| X3 | -,052 | ,608 | -,282 |
| X5 | -,067 | ,462 | ,176 |
Коэффициенты данной матрицы есть не что иное, как коэффициенты корреляции между переменными xi и соответствующими дискриминантными функциями. Так, все независимые переменные отрицательно коррелирут с первой функцией, причем степень корреляции довольно невысока.
Для классификации относительно четырех обучающих выборок было отобрано 10 дополнительных регионов:
| х1 | х2 | х3 | х4 | х5 | х6 | |
| Ростовская область | 1897403,98 | |||||
| Свердловская область | 3293641,16 | |||||
| Челябинская область | 3859178,82 | |||||
| Республика Саха (Якутия) | 2122326,19 | |||||
| Хабаровский край | 1407914,07 | |||||
| Сахалинская область | 33426742,79 | |||||
| Республика Татарстан | 4870539,35 | |||||
| Пермский край | 1269501,23 | |||||
| Нижегородская область | 1570237,56 | |||||
| Кемеровская область | 1177822,01 |
При помощи первой дискриминантной функции определим, к какому кластеру следует отнести каждый из регионов. Коэффициенты дискриминантных функций следующие:
Таблица 37. Нормированные коэффициенты дискриминантных функций
| Функция | |||
| X1 | 5,02 | 2,332 | 1,433 |
| X2 | 0,168 | -1,603 | -3,122 |
| X3 | -2,224 | -1,533 | -0,019 |
| X4 | -1,335 | 2,017 | 0,444 |
| X5 | 1,59 | 0,608 | 1,428 |
| X6 | -3,087 | -0,978 | -0,096 |
Классификация новых объектов по кластерам выглядит следующий образом:
| Регион | Оптимальный кластер | Апостериорная в-ть (1) | Апостериорная в-ть (3) | Апостериорная в-ть (2) | Апостериорная в-ть (4) |
| Ростовская область | 0,0039 | 0,0000 | 0,9962 | ||
| Свердловская область | 0,0000 | 0,0000 | 1,0000 | ||
| Челябинская область | 0,0000 | 0,0000 | 1,0000 | ||
| Республика Саха (Якутия) | 1,0000 | 0,0000 | 0,0000 | ||
| Хабаровский край | 1,0000 | 0,0000 | 0,0000 | ||
| Сахалинская область | 0,0000 | 0,0000 | 0,0000 | ||
| Республика Татарстан | 0,0000 | 1,0000 | 0,0000 | ||
| Пермский край | 0,0000 | 1,0000 | 0,0000 | ||
| Нижегородская область | 0,0000 | 1,0000 | 0,0000 | ||
| Кемеровская область | 0,0000 | 1,0000 | 0,0000 |
Из таблицы видно, что оптимальному кластеру соответствует наибольшая апостериорная вероятность – вероятность попадания в кластер. Таким образом, к единственному «лидеру» по величине значений переменных, влияющих на инвестиции в основные средства, – Республике Дагестан – можно присоединить Сахалинскую область. К отстающим регионам – с наименьшим объемом инвестирования в основные средства – можно отнести Республику Саха (Якутию) и Хабаровский край. Ростовская, Свердловская и Челябинская области попали в кластер с относительно небольшими значениями независимых переменных и, соответственно, уровнем инвестирования в основные средства. В то же время, Нижегородская, Кемеровская области, Пермский край и Республика Татарстан попали в сравнительно «передовой» - третий – кластер.
Аналогичные выводы (аналогичные дискриминантные функции, их нормированные коэффициенты, значения Лямбды-Уилкса, собственные значения, а также аналогичное распределение новых регионов по кластерам) получаются при проведении пошагового алгоритма в SPSS. Поэтому не имеет смысла приводить соответствующие аналитические таблицы еще раз.
Таким образом, в результате дискриминантного анализа были проверены результаты кластерного анализа, а также проведена классификация новых 10 регионов по четырем заданным кластерам.
Выводы
Во второй части данного исследования были проведены компонентный анализ (методом главных компонент), кластерный и дискриминантный анализ. Результатом компонентного анализа является выделение двух главных компонент: z1 - объем собственных и заемных средств, поступивших в предприятия региона за период; z2 - интенсивность вложений предприятий региона в финансовые активы и количества иностранного капитала в регионе. Далее была построена регрессия результирующего показателя Y (объем инвестиций в основные средства) на главные компоненты. Коэффициенты уравнения регрессии получились значимыми, как и само уравнение. Однако по качеству модель регрессии на главные компоненты уступает нелинейной степенной модели (ошибка степенной модели намного ниже, чем ошибка модели главных компонент, в то время как коэффициенты корреляции и детерминации у нелинейной модели выше).
В результате кластерного анализа с помощью различных методов иерархической кластеризации было выведено оптимальное число кластеров, равное 4. Далее методом k-средних была проведена кластеризация 56 регионов относительно заданных 4 кластеров. В первый кластер вошли регионы с самыми низкими значениями показателей, влияющими на Y (32 объекта). В 4 кластер вошел один объект (Республика Дагестан), который характеризуется самыми высокими значениями показателей xi. Расстояния между кластерами оказались достаточно большими, в то время как расстояния между объектами внутри кластера – относительно маленькими. Это говорит об адекватности проведенной кластеризации.
Наконец, дискриминантный анализ подтвердил результаты кластеризации методом k-средних. Далее, на основании наиболее оптимальной функции дискриминации, по соответствующим кластерам были разнесены новые 10 регионов. Результаты метода включения всех переменных сошлись с результатами, полученными при методе пошагового алгоритма. Дискриминантная функция оказалась значимой, следовательно, результаты дискриминантного анализа также можно признать значимыми при заданной надежности.
|
|
|


