Взаимодействие МП и заряженных частиц

Так как всякий ток есть движение заряженных частиц (электронов или ионов), то отсюда следует, что на движущийся заряд в магнитном поле действует сила. На движущуюся в магнитном поле заряженную частицу действует сила

, (14)

где 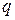— заряд частицы, 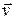— вектор скорости частицы, 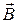— магнитная индукция поля, в котором движется частица. Эту силу называют силой Лоренца.

Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы 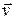и 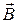. Если заряд положителен, направление силы совпадает с направлением вектора . В случае отрицательного заряда направления векторов и противоположны (рис. 4).

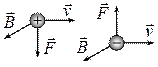
Рис. 4. Действие силы Лоренца на заряды

Поскольку сила Лоренца всегда направлена перпендикулярно к скорости заряженной частицы, она работы не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить её энергию нельзя.

Электромагнитная индукция

Выше отмечено, что электрические токи создают вокруг себя магнитное поле. Существует и обратное явление: магнитное поле вызывает появление электрических токов. Это явление было открыто М. Фарадеем (1831) и получило название электромагнитной индукции.

Суть явления в том, что при изменении потокосцепления, пронизывающего контур (обмотку), наводится электродвижущая сила .

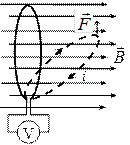
Изменения потокосцепления можно добиться, изменяя число линий магнитной индукции, пересекающих контур. При этом несущественно, чем вызвано изменение потокосцепления — деформацией контура, его перемещением в магнитном поле или изменением самого поля с течением времени. Например, на рис. 5 показан одновитковый контур, находящийся в постоянном магнитном поле. Наклоняя контур, мы изменяем поток через него, при этом вольтметр покажет возникновение индуцированного тока.

Рис. 5. Иллюстрация закона электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея): наведенная ЭДСпрямо пропорциональна и противоположна по знаку скорости изменения потокосцепления контура:

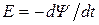. (15)

Знак минус в правой части (15) соответствует правилу Ленца: при всяком изменении потокосцепления контура в нем возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению потокосцепления, вызвавшему индукционный ток. Так, на рис. 5 при наклонении контура в нем возникает ток , который вызывает силу Ампера , препятствующую наклонению контура.

Явление наведения ЭДС в каком-либо контуре при изменении тока, протекающего по этому контуру, называют самоиндукцией. Наведенную ЭДС называют ЭДС самоиндукции.

Магнитная индукция в любой точке поля пропорциональна току в контуре. Поэтому и потокосцепление контура пропорционально току

. (16)

Коэффициент пропорциональности называется индуктивностью. Единицей индуктивности в системе СИ служит генри (Гн). Это индуктивность такого контура, в котором при силе тока 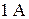возникает магнитный поток .

Подставляя (16) в (15), получаем для ЭДС самоиндукции выражение

. (17)

ЭДС самоиндукции пропорциональна скорости изменения тока.

Опыт показывает, что индуктивность какого-либо контура зависит не только от его формы и размеров, но и от свойств среды в которой он находится. Пусть — индуктивность контура в вакууме, а — индуктивность того же контура в однородном веществе, заполняющем все магнитное поле. Отношение

(18)

называют относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. Очевидно, что 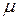— безразмерная величина. Магнитная проницаемость есть величина, характеризующая магнитные свойства вещества, она зависит от рода вещества и его состояния (например, от температуры).

Величина называется абсолютной магнитной проницаемостью. Размерность у 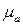такая же, как и у , т.е. .

В среде с магнитной проницаемостью 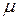при том же токе в контуре индукция в 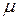раз больше, чем в вакууме:

. (19)

Атом в магнитном поле

Все тела при внесении их во внешнее МП намагничиваются в той или иной степени, т.е. создают собственное МП, которое накладывается на внешнее поле. Магнитные свойства вещества определяются магнитными свойствами электронов и атомов.

Рис. 6. Магнитный и механический моменты электрона

Электрон, движущийся по орбите в атоме, эквивалентен замкнутому контуру с орбитальным током (рис. 6). Если электрон совершает оборотов в секунду, то сила тока равна , где 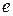— заряд электрона. Магнитный момент такого “витка” с током называется орбитальным магнитным моментом электрона. Он равен

,

где — площадь, ограниченная орбитой. Если, как показано на рис. 6, электрон обращается по часовой стрелке, то ток направлен против часовой стрелки (заряд электрона отрицательный) и орбитальный магнитный момент направлен, в соответствии с правилом правого буравчика, перпендикулярно к плоскости орбиты снизу вверх.

Электрон, движущийся по орбите, обладает орбитальным механическим моментом импульса

, (20)

где — масса электрона, — угловая скорость электрона, — радиус орбиты электрона. Направление также подчиняется правилу буравчика. Из рис. 6 видно, что направления и противоположно. Отношение орбитального магнитного момента электрона к его механическому моменту равно

. (21)

Это отношение называется гиромагнитным отношением орбитальных моментов. В (21) знак минус выражает противоположность направлений и . Гиромагнитное отношение полностью определяется универсальными постоянными, т.е. зарядом и массой электрона.

Кроме того, при движении по орбите каждый электрон обладает свойством, близким к свойствам заряженного тела, вращающегося вокруг своей оси. Это свойство называют спином электрона. Спин электрона, обусловливает спиновый магнитный момент (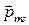 на рис. 6). Важнейшей особенностью спинового магнитного момента электрона является наличие только двух его проекций на направление вектора 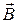индукции магнитного поля

, (22)

где , — постоянная Планка, — магнетон Бора, являющийся единицей измерения магнитных моментов.

Протоны и нейтроны, входящие в ядро атома, тоже имеют некоторые магнитные моменты, но они в сотни раз меньшие, чем электроны. Поэтому обычно их влиянием пренебрегают.

Соотношения (20) – (22) справедливы для каждого из электронов в атоме. Число совпадает с порядковым номером химического элемента в периодической системе Менделеева.

Орбитальным магнитным моментом атома называется векторная сумма орбитальных магнитных моментов всех его электронов

.

Орбитальным моментом импульса атома называется векторная сумма орбитальных моментов импульса всех электронов

.

Атомные моменты и связаны соотношением .

Рис. 7. Ларморова прецессия

Рассмотрим поведение атома под воздействием внешнего МП. Электрон, вращающийся вокруг ядра, можно представить в виде своеобразного волчка, который, двигаясь по орбите, образует замкнутый ток и обладает определенным магнитным моментом (рис. 7,а). Из-за того, что в МП на движущийся электрон действует сила Лоренца, стремящаяся ориентировать плоскость электронной орбиты перпендикулярно к полю 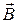, волчок будет совершать прецессионное движение, т.е. получит дополнительное равномерное вращение, при котором вектор будет описывать конус вокруг направления индукции 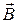с некоторой угловой скоростью (рис. 7,а). Такая угловая скорость называется частотой ларморовской прецессии и равна

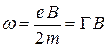. (23)

Эта скорость не зависит от ориентировки орбиты, т.е. от угла между векторами и .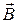

Прецессия электронной орбиты эквивалентна некоторому дополнительному вращению электрона, которое вследствие наличия у него электрического заряда дает дополнительный магнитный момент (рис. 7,б). Дополнительный магнитный момент ориентирован всегда против поля.

Теорема Лармора: действие МП на движущийся электрон в атоме не вызывает непосредственно переориентацию электронных орбит, а вызывает только их прецессию.

Магнитное поле в веществе

Из изложенного следует, что атомов, на которые бы не действовало МП, не существует. Все вещества в МП в той или иной степени намагничиваются. Намагниченность можно рассматривать как напряженность, создаваемую атомами вещества под действием внешнего МП. Единица намагниченности есть ампер на метр (А/м). 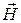Напряженность внутри вещества можно найти, суммируя собственную намагниченность с напряженностью внешнего МП. Поэтому индукцию 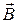в веществе можно представить как

. (24)

Разделим обе части равенства (24) на : .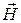

Отношение называют магнитной восприимчивостью вещества – :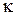

, (25)

где 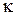— скалярная величина, зависящая от магнетика. Из сравнения (19), (24) и (25) следует, что

. (26)

По поведению в МП все вещества можно разделить на диамагнетики и парамагнетики. У диамагнетиков магнитная восприимчивость отрицательна (), а у парамагнетиков положительна (). Парамагнетики, в свою очередь, можно разделить на собственно парамагнетики, ферромагнетики, ферриты и антиферромагнетики.

В диамагнитных веществах орбитальные и спиновые магнитные моменты всех электронных орбит взаимно скомпенсированы и суммарный магнитный момент атома равен нулю. Диамагнетики в отсутствии внешнего МП не обладают собственным магнитным моментом, а в поле приобретают магнитный момент, направленный против внешнего поля (отсюда 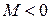и ). Последнее связано с тем, что под действием внешнего МП электронные орбиты атома совершают прецессионное движение, которое эквивалентно круговому току , и у атома появляется составляющая МП, направленная противоположно внешнему полю (рис. 7).

Диамагнетиками являются, например, все инертные газы. Величина диамагнитной восприимчивости растет с увеличением порядкового номера в таблице Менделеева. Это можно объяснить тем, что чем выше порядковый номер элемента, тем больше в атоме электронов и, следовательно, большее число электронных орбит будет прецессировать вокруг направления поля, создавая отрицательную намагниченность. Также диамагнетиками являются водород, азот, многие металлы (), большинство органических соединений, смолы, углерод и т.д.

В остальных веществах атомы обладают магнитным моментом. При помещении этих веществ в магнитное поле они приобретают суммарный магнитный момент (намагниченность), направленный вдоль внешнего поля.

Парамагнетиком называется вещество, у которого в отсутствие МП магнитные моменты атомов ориентированы хаотически (суммарный момент равен нулю). Под воздействием внешнего МП магнитные моменты атомов начинают ориентироваться вдоль направления поля и появляется намагниченность, величина которой в не очень сильных магнитных полях пропорциональна индукции внешнего поля.

В отсутствие МП магнитные моменты атомов в парамагнетике вследствие теплового движения ориентированы совершенно беспорядочно. И чем выше температура, тем труднее ориентируются магнитные моменты атомов под воздействием МП. Закон Кюри: магнитная восприимчивость парамагнетика обратно пропорциональна абсолютной температуре, т.е. , где — постоянная, 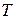— абсолютная температура.

Магнитная восприимчивость k у диа- и парамагнетиков весьма мала (порядка 10^–3 ¸10^–4). Поэтому магнитная проницаемость 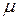близка к единице и все диа- и парамагнитные вещества намагничиваются весьма слабо.

Рис. 8. Ориентация доменов без внешнего МП

Ферромагнетик внутри обычно разбивается на макроскопические малые (размером ) области — домены, внутри которых атомные магнитные моменты сонаправлены и намагниченность велика. Домен можно представить как мельчайший магнитик. В веществе домены выстраиваются таким образом, чтобы энергия, заключенная в их МП, была минимальна. На рис. 8 приведен пример расположения доменов в ферромагнетике при отсутствии внешнего МП. Здесь сверху и снизу рисунка есть замыкающие домены, вследствие этого магнитный поток проходит исключительно внутри ферромагнетика и МП вещества будет незаметно.

Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля.

Различные фазы намагничивания представлены на рис. 9. В отсутствие внешнего МП ферромагнетик разбивается на домены таким образом, что его результирующий магнитный момент близок к нулю. Это схематически показано на рис. 9,а. При появлении внешнего поля, направленного так, как показано на рис. 9 вверху, происходит смещение границ доменов, при котором объем доменов, направленных против МП, уменьшается (рис. 9,б). Этой фазе соответствует область 1 на кривой намагничивания рис. 9,е.

Рис. 9. Фазы намагничивания ферромагнетика

При дальнейшем увеличении напряженности МП происходит исчезновение границ доменов (рис. 9,в). Этому соответствует область 2кривой намагничивания (рис. 9,е).

Если поле увеличивать еще больше, то будет изменяться направление магнитного момента внутри домена (намагничивание вращения, рис. 9,г; этому соответствует область 3на рис. 9,е).

Наконец, в очень сильном поле магнитные моменты всех доменов установятся параллельно полю. В этом состоянии ферромагнетик имеет наибольший возможный при данной температуре магнитный момент, т.е. намагничен до насыщения (рис. 9,д). Возникшая при этом индукция в сердечнике называется индукцией технического насыщения (рис. 10).

Рис. 10. Петля гистерезиса ферромагнетика

Техническое насыщение достигается при напряженности (рис. 10). Если после этого уменьшить до нуля напряженность внешнего МП, то не все домены вернутся к прежней ориентации, некоторые останутся ориентированными близко к направлению «выключенного» внешнего поля, материал будет иметь остаточную индукцию. Магнетики, у которых отношение близко к единице, называют магнитотвердыми. Остаточная индукция особенно велика у сплавов магния, никеля, кобальта, из которых изготавливают постоянные магниты.

Для того чтобы сделать намагниченность ферромагнетика нулевой, необходимо приложить магнитное поле противоположного направления. Напряженность такого поля называют коэрцитивной силой . Увеличивая обратное поле, затем уменьшая его и накладывая в первоначальном направлении, т.е. изменяя его величину и направление периодически, можно получить в координатах петлю гистерезиса (рис. 10).

Кристаллическая решетка антиферромагнетика состоит из двух подрешеток, намагниченных противоположно. Из-за этого магнитные моменты этих подрешеток оказываются взаимно скомпенсированы. В ферримагнетиках (ферритах) эта компенсация оказывается не полной. Схематическая ориентация магнитных моментов антиферромагнетиков и ферримагнетиков представлена в табл. 1.

	Таблица 1
Тип магнетика	Индукция внешнего МП B = 0	B > 0
Взаимная ориентация магнитных частиц вещества	Суммарный магнитный момент
Диамагнетик		M = 0	M < 0
Парамагнетик		M = 0	M > 0
Ферромагнетик		M > 0
Антиферро-магнетик	или	M = 0
Ферримагнетик		M > 0

Ферромагнетики и ферриты широко используются для изготовления трансформаторов, дросселей, различных датчиков. На высоких частотах ферриты имеют преимущество, т.к. обладают большим удельным электрическим сопротивлением и из-за этого у них меньшие потери на вихревые токи.

В табл. 1 представлены ориентация магнитных моментов и их результирующие магнитные моменты для всех рассмотренных нами магнетиков без внешнего МП и с ним.

Тепловое движение мешает упорядочению расположения магнитных моментов атомов в кристаллической решетке, и, кроме того, с ростом температуры меняются расстояния между атомами, поэтому при определенной для каждого ферромагнетика температуре (она называется температурой или точкой Кюри) он теряет свои особые магнитные свойства и становится парамагнетиком.

Магнитострикция — изменение размеров и формы образца при наложении МП. Возникающие при этом деформации весьма малы: обычно имеют порядок 10^–5–10^–6. Магнитострикция зависит от намагниченности, последняя же изменяется от температуры, поэтому величина магнитострикции также изменяется с температурой, обращаясь в точке Кюри в ноль. Магнитострикция не зависит от знака намагниченности.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: