 |
Определение срока ссуды и величины процентной ставки
|
|
|
|
В любой простейшей финансовой операции всегда присутствуют четыре величины: современная величина (PV), наращенная или будущая величина (FV), процентная ставка (i) и время (n).
Иногда при разработке условий финансовой сделки или ее анализе возникает необходимость решения задач, связанных с определением отсутствующих параметров, таких как срок финансовой операции или уровень процентной ставки.
Как правило, в финансовых контрактах обязательно фиксируются сроки, даты, периоды начисления процентов, поскольку фактор времени в финансово-коммерческих расчетах играет важную роль. Однако бывают ситуации, когда срок финансовой операции прямо в условиях финансовой сделки не оговорен, или когда данный параметр определяется при разработке условий финансовой операции.
Обычно срок финансовой операции определяют в тех случаях, когда известна процентная ставка и величина процентов.
Если срок определяется в годах, то
n = (FV - PV): (PV • i),
а если срок сделки необходимо определить в днях, то появляется временная база в качестве сомножителя:
t = [(FV - PV): (PV • i)] • T.
Пример 6. На сколько дней можно дать в долг 1'000 долларов, исходя из 8% годовых, если возвращенная сумма будет составлять 1'075 долларов?
Решение:
Исходя из формулы срока долга для простых процентов, следует:
для обычных процентов
t = [(FV - PV): (PV • i)] • T =
= [(1'075 - 1'000): (1'000 • 0,08) • 360 = 338 дней;
для точных процентов
t = [(FV - PV): (PV • i)] • T =
= [(1'075 - 1'000)/(1'000 • 0,08) • 365 = 342 дня.
Таким образом, сумма в 1'000 долларов может быть предоставлена на срок в 342 дня, если в условиях финансовой операции будет использован термин "точные проценты", а по умолчанию или использованию термина "обыкновенные проценты", срок ссуды сокращается до 338 дней.
|
|
|
Необходимость определения уровня процентной ставки возникает в тех случаях, когда она в явном виде в условиях финансовой операции не участвует, но степень доходности операции по заданным параметрам можно определить, воспользовавшись следующими формулами:
i = (FV - PV): (PV • n) = [(FV - PV): (PV • t)] • T.
Пример 7. В контракте предусматривается погашение обязательств через 120 дней в сумме 1'200 долларов, при первоначальной сумме долга 1'150 долларов. Определить доходность операции для кредитора в виде процентной ставки.
Решение:
Рассчитываем годовую процентную ставку, используя формулу "обыкновенного процента", поскольку в условиях сделки нет ссылки на "точный процент":
i = [(FV - PV): (PV • t)] • T =
= [(1'200 - 1'150): (1'150 • 120)] • 360 = 0,13
Таким образом, доходность финансовой операции составит 13% годовых, что соответствует весьма высокодоходной финансовой операции, т.к. обычно доходность подобных операций колеблется от 2% до 8%.
Формула сложных процентов
В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов.
Применение схемы сложных процентов целесообразно в тех случаях, когда:
- проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;
- срок ссуды более года.
Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:
FV = PV + I = PV + PV • i = PV • (1 + i)
– за один период начисления;
FV = (PV + I) • (1 + i) = PV • (1 + i) • (1 + i) = PV • (1 + i)2
– за два периода начисления;
|
|
|
отсюда, за n периодов начисления формула примет вид:
FV = PV • (1 + i) n = PV • kн,
где FV – наращенная сумма долга;
PV – первоначальная сумма долга;
i – ставка процентов в периоде начисления;
n – количество периодов начисления;
kн – коэффициент (множитель) наращения сложных процентов.
Эта формула называется формулой сложных процентов.
Как было выше указано, различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу. Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучаемого явления с постоянными абсолютными приростами. Сложные проценты характеризуют процесс роста первоначальной суммы со стабильными темпами роста, при наращении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста.
Согласно общей теории статистики, для получения базисного темпа роста необходимо перемножить цепные темпы роста. Поскольку ставка процента за период является цепным темпом прироста, то цепной темп роста равен:
(1 + i).
Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста, имеет вид:
(1 + i) n.
Базисные темпы роста или коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы и представлены в Приложении 2. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке i. 5>>>
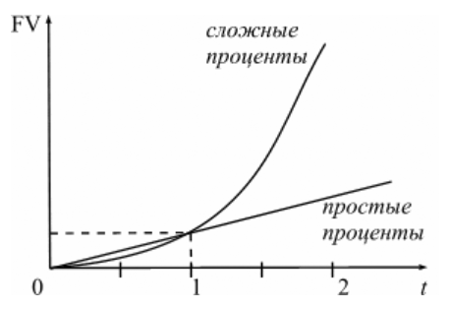
Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рисунке 4.
|
| Рис. 4. Наращение по простым и сложным процентам. |
Как видно из рисунка 4, при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.
|
|
|
При любом i,
если 0 < n < 1, то (1 + ni) > (1 + i) n;
если n > 1, то (1 + ni) < (1 + i) n;
если n = 1, то (1 + ni) = (1 + i) n.
Таким образом, для лиц, предоставляющих кредит:
- более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);
- более выгодной является схема сложных процентов, если срок ссуды превышает один год;
- обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.
Пример 8. Сумма в размере 2'000 долларов дана в долг на 2 года по ставке процента равной 10% годовых. Определить проценты и сумму, подлежащую возврату.
Решение:
Наращенная сумма
FV = PV • (1 + i) n = 2'000 • (1 + 0'1)2 = 2'420 долларов
или
FV = PV • kн = 2'000 • 1,21 = 2'420 долларов,
где kн = 1,21 (Приложение 2).
Сумма начисленных процентов
I = FV - PV = 2'420 - 2'000 = 420 долларов. 6>>>
Таким образом, через два года необходимо вернуть общую сумму в размере 2'420 долларов, из которой 2'000 долларов составляет долг, а 420 долларов – "цена долга".
Достаточно часто финансовые контракты заключаются на период, отличающийся от целого числа лет.
В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов:
- общий метод заключается в прямом расчете по формуле сложных процентов:
FV = PV • (1 + i) n,
n = a + b,
где n – период сделки;
a – целое число лет;
b – дробная часть года.
- смешанный метод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов:
FV = PV • (1 + i) a • (1 + bi).
Поскольку b < 1, то (1 + bi) > (1 + i) a, следовательно, наращенная сумма будет больше при использовании смешанной схемы.
Пример. В банке получен кредит под 9,5% годовых в размере 250 тыс. долларов со сроком погашения через два года и 9 месяцев. Определить сумму, которую необходимо вернуть по истечении срока займа двумя способами, учитывая, что банк использует германскую практику начисления процентов.
|
|
|
Решение:
Общий метод:
FV = PV • (1 + i) n = 250 • (1 + 0,095)2,9 = 320,87 тыс. долларов.
Смешанный метод:
FV = PV • (1 + i) a • (1 + bi) =
= 250 • (1 + 0,095)2 • (1 + 270/360 • 0,095) =
= 321,11 тыс. долларов.
Таким образом, по общему методу проценты по кредиту составят
I = S - P = 320,87 - 250,00 = 70,84 тыс. долларов, 7>>>
а по смешанному методу
I = S - P = 321,11 - 250,00 = 71,11 тыс. долларов.
Как видно, смешанная схема более выгодна кредитору.

| <<<5 | При пользовании финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки. |
| <<<6 | Сравните полученный результат с результатом примера 1. Не трудно заметить, что сложная ставка дает большую сумму процентов. |
| <<<7 | При расчете по смешанному методу результат всегда оказывается больше. |
|
|
|


