 |
Линейного программирования
|
|
|
|
Данный метод применяется для решения задач, содержащих не более трех переменных, чаще всего для задач с двумя переменными. Он базируется на следующих моментах:
§ множество допустимых решений задачи выпукло, в линейном случае оно представляет собой конечный или простирающийся в бесконечность многоугольник;
§ целевая функция достигает своего оптимального значения в вершине области. Если она принимает это значение в двух вершинах области, то оптимум достигается в любой точке отрезка, соединяющего эти вершины;
§ направляющий вектор (вектор нормали) перпендикулярен прямой функции цели и всегда указывает направление ее возрастания.
Схему применения графического метода проиллюстрируем на конкретном примере, рассматривая три этапа:
§ построение области допустимых решений;
§ построение направляющего вектора и определение оптимальных точек;
§ нахождение оптимальных значений переменных и целевой функции.
Найти максимальное и минимальное значение функции

при ограничениях

І этап. Построение области допустимых решений
1. Каждому неравенству ставим в соответствие равенство, геометрическим образом которого является прямая линия. Для ее построения достаточно двух точек.
§ 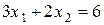 - эта прямая пройдет через точки (2; 0) и (0; 3).
- эта прямая пройдет через точки (2; 0) и (0; 3).

| 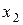
|
§  - эта прямая пройдет через точки (-3; 0) и (0; 2).
- эта прямая пройдет через точки (-3; 0) и (0; 2).

| 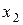
|
| – 3 |
§ 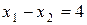 - эта прямая пройдет через точки (4; 0) и (0; -4).
- эта прямая пройдет через точки (4; 0) и (0; -4).

| 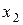
|
| – 4 | |
§  - эта прямая пройдет через точки (7; 0) и (0; 4).
- эта прямая пройдет через точки (7; 0) и (0; 4).

| 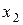
|
2. Каждая прямая делит плоскость на две полуплоскости, в одной из которых будет справедливо соответствующее неравенство. Чтобы установить, точки какой полуплоскости будут обеспечивать выполнение неравенства, необходимо взять произвольную точку и ее координаты подставить в неравенство. Если для этой точки неравенство выполнилось, то решением неравенства будет та полуплоскость, в которой брали точку. Если неравенство для выбранной точки не выполнилось, то его решением будут точки второй полуплоскости. Рассматривая поочередно все ограничения, получим область, в которой будут справедливы все неравенства, - это и есть область допустимых решений.
|
|
|

Неравенства 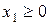 и
и  означают, что область будет находиться в первой четверти. В нашем случае областью допустимых решений являются точки пятиугольника
означают, что область будет находиться в первой четверти. В нашем случае областью допустимых решений являются точки пятиугольника  .
.
ІІ этап. Определение оптимальных точек
1. Направляющий вектор проводят из начала координат в точку с координатами, равными коэффициентам целевой функции, то есть в точку  . Он всегда указывает направление возрастания функции, направление убывания целевой функции будет противоположным.
. Он всегда указывает направление возрастания функции, направление убывания целевой функции будет противоположным.
2. Перпендикулярно направляющему вектору на области допустимых решений проводят прямую  (она показана пунктиром).
(она показана пунктиром).
3. Если в задаче требуется найти максимум, прямую  перемещают параллельно в сторону стрелки направляющего вектора до последней точки области – эта точка и будет точкой максимума. В примере наибольшее значение достигается в вершине
перемещают параллельно в сторону стрелки направляющего вектора до последней точки области – эта точка и будет точкой максимума. В примере наибольшее значение достигается в вершине  .
.
4. Если требуется найти минимум, то прямую  перемещают параллельно в противоположную сторону до последней точки области. В данном случае наименьшее значение достигается в вершине
перемещают параллельно в противоположную сторону до последней точки области. В данном случае наименьшее значение достигается в вершине  .
.
ІІІ этап. Нахождение оптимальных значений
Чтобы найти переменные, обеспечивающие экстремум, необходимо решить систему уравнений тех прямых, на пересечении которых располагается точка экстремума
а) находим 
| б) находим 
|




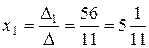

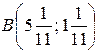

| 







|
Таким образом, найдены максимальное и минимальное значение функции, все промежуточные значения будут достигаться в других точках области допустимых значений.
|
|
|
Замечание 1. Если прямая функции  окажется параллельной какой-нибудь стороне многоугольника ограничений, то в этом случае задача имеет бесчисленное множество решений: координаты любой точки этой стороны многоугольника (в том числе и вершины) будут решением задачи.
окажется параллельной какой-нибудь стороне многоугольника ограничений, то в этом случае задача имеет бесчисленное множество решений: координаты любой точки этой стороны многоугольника (в том числе и вершины) будут решением задачи.
Замечание 2. Если область решений не ограничена, то задача или не имеет решения, или целевая функция может принять только максимальное или только минимальное значение, или задача имеет бесконечное множество решений.
Симплексный метод
Симплексный метод является универсальным методом решения задач линейного программирования.
Его алгоритм в той или иной интерпретации содержится практически во всех учебниках и учебных пособиях по этой дисциплине. Следует при этом учесть, что решение нужно начинать с приведения задачи к каноническому виду. Решение осуществляется в три этапа:
а) строится начальное решение;
6) проводится оценка найденного решения по соответствующему критерию оптимальности;
в) если условие оптимальности не выполняется, переходят к новому решению.
Этапы б) и в) выполняются до тех пор, пока будет получено оптимальное решение.
Все правила проиллюстрируем на примере:
Найти  , при ограничениях
, при ограничениях


I этап. Построение начального решения.
а) Приводим задачу к каноническому виду.
1. Необходимо перейти к нахождению минимума, чтобы все правила рассмотреть для этого случая. Если в условии требуется найти максимум, то переходят к минимуму противоположной функции, а, решив задачу, возвращаются к заданной функции цели. В указанном примере:

2. Если среди свободных членов в системе ограничений есть отрицательные, то соответствующие ограничения умножают на (–1). В нашем случае это правило относится к ІІІ-му ограничению. В результате его применения система станет такой:

3. Если среди ограничений есть неравенства, то, вводя дополнительные переменные, преобразуют их в уравнения. В нашем случае:
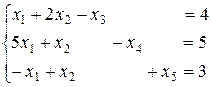



Получили канонический вид задачи.
б) В ограничения, где дополнительные переменные вычитаются, добавляют искусственные переменные с последующими номерами. Эти искусственные неизвестные вносят и в целевую функцию с коэффициентом  . В результате таких преобразований задача приобретет вид:
. В результате таких преобразований задача приобретет вид:
|
|
|

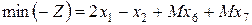 ,
,
где 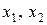 – основные переменные;
– основные переменные;
 – дополнительные переменные;
– дополнительные переменные;
 – искусственные переменные.
– искусственные переменные.
Все переменные – неотрицательны.
в) Выписывают векторы коэффициентов при неизвестных и вектор свободных членов.








г) строят первую симплексную таблицу следующего вида:
Таблица 1
| Базис | 
| 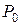
| - 1 | 
| 
| С.О. | ||||
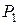
| 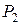
| 
| 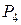
| 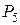
| 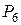
| 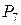
| ||||
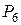
| 
| -1 | ||||||||
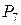
| 
| -1 | ||||||||
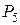
| -1 | - | ||||||||
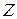 -строка -строка
| -2 | |||||||||
 -строка -строка
| -1 | -1 |
Заполняют таблицу по правилам:
1. Вносят все векторы  .
.
2. В самую верхнюю строку записывают коэффициенты целевой функции при соответствующих неизвестных.
3. В качестве первоначального базиса берут векторы, образующие единичную матрицу, - в данном случае это векторы 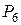 ,
, 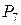 ,
, 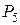 .
.
4. В столбец  переносят из верхней строки числа, соответствующие базисным векторам.
переносят из верхней строки числа, соответствующие базисным векторам.
5. Чтобы получить элементы двух последних строк, вектор  умножают последовательно на векторы
умножают последовательно на векторы 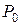 ,
, 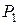 ,…,
,…, 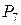 и от результата вычитают соответствующее число из верхней строки
и от результата вычитают соответствующее число из верхней строки

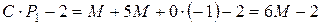


| 



|
В  -строку записывают коэффициенты при
-строку записывают коэффициенты при  , в
, в 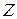 -строку – коэффициенты без
-строку – коэффициенты без  .
.
д) После того, как составлена симплекс-таблица, можно записать решение. Оно всегда содержится в столбце 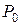 и соответствует переменным с номерами базисных векторов. Неизвестные, векторы которых не входят в базис, равны нулю. В данном случае имеем:
и соответствует переменным с номерами базисных векторов. Неизвестные, векторы которых не входят в базис, равны нулю. В данном случае имеем:
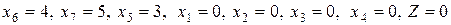 .
.
ІІ этап. Проверка оптимальности решения
а) Критерий оптимальности: функция достигает минимума, если среди элементов  -строки (а затем
-строки (а затем 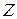 -строки), начиная со второго, нет положительных чисел. В противном случае необходимо улучшать решение.
-строки), начиная со второго, нет положительных чисел. В противном случае необходимо улучшать решение.
Следуя данному критерию, можем заключить, что полученное из таблицы 1 решение не является оптимальным: в  -строке есть 2 положительных числа – это 6 и 3.
-строке есть 2 положительных числа – это 6 и 3.
б) В случае, когда критерий оптимальности не выполняется, выбирают ключевой столбец – по наибольшему положительному числу в  -строке (а затем в
-строке (а затем в 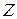 -строке), начиная со второго. Ключевой столбец показывает, какой вектор войдет в новый базис. В таблице 1 – наибольшее число в
-строке), начиная со второго. Ключевой столбец показывает, какой вектор войдет в новый базис. В таблице 1 – наибольшее число в  -строке (начиная со второго) равно 6, в новый базис войдет
-строке (начиная со второго) равно 6, в новый базис войдет 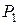 .
.
|
|
|
в) Определяют симплексные отношения, для этого элементы 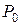 делят на положительные элементы ключевого столбца (на отрицательные и нули не делят). В таблице 1 симплексные отношения равны 4 и 1, в третьей строке ставят прочерк, т.к. на (– 1) не делят.
делят на положительные элементы ключевого столбца (на отрицательные и нули не делят). В таблице 1 симплексные отношения равны 4 и 1, в третьей строке ставят прочерк, т.к. на (– 1) не делят.
г) Ключевую строку выбирают по наименьшему симплексному отношению (С.О.), она показывает, какой вектор выйдет из базиса. Наименьшее симплексное отношение равно 1, ключевой будет вторая строка, из базиса уйдет искусственный вектор 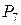 .
.
д) Элемент, стоящий на пересечении ключевой строки и ключевого столбца, называется генеральным. В построенной таблице генеральный элемент равен 5.
III этап. Построение нового решения (таблицы 2).
а) Формируют новый базис, заменяя вектор 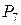 на вектор
на вектор 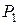 . В данной задаче новый базис будет состоять из векторов
. В данной задаче новый базис будет состоять из векторов 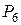 ,
, 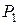 ,
, 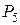 . Поскольку из базиса вышел искусственный вектор
. Поскольку из базиса вышел искусственный вектор 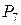 , то соответствующий ему столбец следует отбросить. Когда из базиса уходит последний искусственный вектор, то отбрасывают и
, то соответствующий ему столбец следует отбросить. Когда из базиса уходит последний искусственный вектор, то отбрасывают и  -строку.
-строку.
б) Столбец  заполняют по правилу, изложенному выше – из верхней строки.
заполняют по правилу, изложенному выше – из верхней строки.
Таблица 2
| Базис | 
| 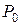
| - 1 | 
| С.О. | ||||
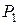
| 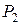
| 
| 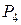
| 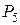
| 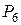
| ||||
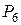
| 
| 9/5 | -1 | 1/5 | 5/3 | ||||
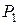
| 1/5 | -1/5 | |||||||
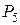
| 6/5 | -1/5 | 10/3 | ||||||
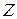 -строка -строка
| 7/5 | -2/5 | |||||||
 -строка -строка
| 9/5 | -1 | 1/5 |
в) Вычисления ведут по таким правилам.
1. Элементы ключевой строки делят на генеральный элемент и записывают в новую таблицу.
2. Ключевой столбец дополняют нулями.
3. Если в ключевой строке есть нули, то соответствующие им столбцы переносят без изменения – это  .
.
4. Остальные элементы определяют по правилу прямоугольника. Для его построения в предыдущей таблице старый элемент соединяют с ключевой строкой и ключевым столбцом, а затем по строке и столбцу ведут к генеральному элементу, (см. табл. 1)

| 
| ||

| |||
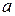
| 
|
 – генеральный элемент,
– генеральный элемент, 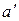 – новый элемент,
– новый элемент, 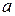 – старый элемент,
– старый элемент,  – элемент ключевой строки,
– элемент ключевой строки,  – элемент ключевого столбца.
– элемент ключевого столбца.
Новый элемент находят так: вычисляют произведение элементов диагонали, содержащей генеральный элемент, из него вычитают произведение элементов другой диагонали; полученною разность делят на генеральный элемент, и результат вносят в новую таблицу (см. табл. 2).
Например, для столбца 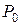 имеем:
имеем:
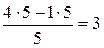



Для столбца 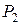 получим:
получим:
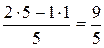

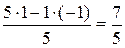

Решение, соответствующее ІІ-й таблице, берем из 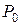 , оно имеет вид:
, оно имеет вид:
|
|
|
 .
.
Для анализа второго решения повторяют все действия, начиная со II этапа. Проверка показала, что во II таблице условие оптимальности не выполняется: есть два положительных числа – это 9/5 и 1/5. Берут наибольшее и выделяют ключевой столбец  , находят симплексные отношения и выбирают ключевою строку (первая), генеральный элемент равен 9/5. Все вычисления приводят к таблице 3. Из базиса уходит последний искусственный вектор
, находят симплексные отношения и выбирают ключевою строку (первая), генеральный элемент равен 9/5. Все вычисления приводят к таблице 3. Из базиса уходит последний искусственный вектор  , поэтому таблица 3 не будет содержать столбец
, поэтому таблица 3 не будет содержать столбец  и
и  -строку.
-строку.
Таблица 3
| Базис | 
| 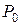
| - 1 | С.О. | ||||
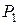
| 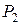
| 
| 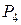
| 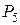
| ||||

| -1 | 5/3 | -5/9 | 1/9 | - | |||
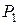
| 2/3 | 1/9 | -2/9 | |||||
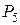
| 2/3 | -1/3 | ||||||
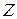 -строка -строка
| -1/3 | 7/9 | -5/9 |
Решение в соответствии с таблицей 3 имеет вид:
 .
.
Данное решение оптимальным не является – проверку ведем по 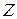 -строке, в ней содержится положительное число 7/9. Строим еще одну таблицу.
-строке, в ней содержится положительное число 7/9. Строим еще одну таблицу.
Таблица 4
| Базис | 
| 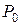
| - 1 | ||||
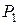
| 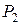
| 
| 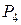
| 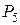
| |||

| -1 | 10/3 | -1/6 | 5/6 | |||
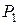
| 1/3 | -1/6 | -1/6 | ||||
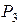
| -1/2 | 3/2 | |||||
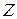 -строка -строка
| -8/3 | -1/6 | -7/6 |
В 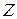 -строке среди элементов, начиная со второго, нет положительных чисел, значит, в табл. 4 условие оптимальности выполнилось. Оптимальное решение имеет вид:
-строке среди элементов, начиная со второго, нет положительных чисел, значит, в табл. 4 условие оптимальности выполнилось. Оптимальное решение имеет вид:
 .
.
Дадим геометрическую интерпретацию симплексному решению. Для этого построим область допустимых решений и проанализируем, каким точкам соответствует каждая симплекс-таблица. В расчет берем только значения основных переменных  и
и  .
.

Область решений не является конечной, а простирается в бесконечность и содержит бесчисленное множество точек, для которых выполняются все ограничения.
Первой симплекс-таблице соответствуют значения 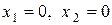 , это точка
, это точка 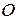 – она не лежит в области решений, т.к. в таблице присутствуют искусственные переменные. Второй таблице соответствуют
– она не лежит в области решений, т.к. в таблице присутствуют искусственные переменные. Второй таблице соответствуют 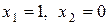 это точка
это точка 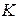 , она тоже находится вне области решений. В третьей таблице искусственные переменные исключены, поэтому решение уже принадлежит области решений:
, она тоже находится вне области решений. В третьей таблице искусственные переменные исключены, поэтому решение уже принадлежит области решений:  – это точка
– это точка  . Данная вершина не является оптимальной, мы переходим к четвертой таблице и к вершине
. Данная вершина не является оптимальной, мы переходим к четвертой таблице и к вершине  :
:  .
.
|
|
|


