 |
Диапазоны целевых коэффициентов
|
|
|
|
| Переменные ------------------------ | Нижний предел –––––––––––––––– | Текущее значение –––––––––––––––––– | Верхний предел ------------------------ |
| XI | -5.0 | 3.0 | 4.4 |
| Х2 | 3.4 | 5.0 | нет |
| Диапазон правых частей | |||
| Ограничение ------------------------ | Нижний предел ------------------------ | Текущее значение ------------------------ | Верхний предел ------------------------ |
| нет | 10.0 | 19.2 | |
| -0.0 | 4.0 | 7.0 | |
| 36.3 | 56.0 | 60.0 | |
| 52.0 | 56.0 | нет | |
| -23.2 | 15.0 | нет |
Аналогичным образом вводятся и решаются задачи пакета. В целочисленных задачах, к примеру, добавляется меню типизации переменных: будут ли все переменные целыми или только какая-то часть из них. В транспортных задачах и задачах о назначении ввод данных проводится по строкам в режиме диалога и занимает значительное время, но это вполне оправдано быстротой решения и т.д.
Пакет QSB
В этом пакете реализуется количественные методы в экономике, поэтому он может быть использован в разных разделах математики. С его помощью решаются задачи линейного, целочисленного, квадратического и динамического программирования, распределительные задачи, сетевые модели и другие проблемы.
Использование пакета происходит в режиме диалога. Уточняется дата, время. Нажимая клавишу ENTER, приходят к Главному меню пакета (рис. 6).
| 1. Линейное программирование | A– | Динамическое программирование |
| 2. Целочисленное программирование | B – | Управление запасами |
| 3. 2-х-целевое программирование | C – | Теория массового обслуживания |
| 4. Квадратическое программирование | D – | Имитационное моделирование |
| 5. Транспортная задача | E – | Теория вероятностей |
| 6. Задача о назначении и коммивояжере | F – | Марковские процессы |
| 7. Сетевое программирование | G – | Прогнозирование временных рядов |
| 8. Проектирование расписаний (I) (CPM) | H – | Настройка аппаратуры |
| 9. Проектирование (II) (PERT) | J – | Выход из QSB |
|
|
|
Рисунок 6 – Главное меню пакета
Для выбора нужного модуля необходимо на клавиатуре нажать соответствующую цифру или букву. После этого появится функциональное меню. Например, нажав цифру 1, попадаем в модуль линейного программирования и получаем такое Меню функции (рис. 7).
| Функции | ||
| – | Краткий обзор системы LP | |
| – | Ввод новой задачи | |
| – | Чтение задачи с диска | |
| – | Просмотр введенных данных | |
| – | Решение задачи | |
| – | Сохранение задачи на диске | |
| – | Корректировка условия задачи | |
| – | Просмотр решения | |
| – | Возврат к Главному меню | |
| – | Выход из пакета |
Рисунок 7 – Меню функции для линейного программирования
Функция набирается нажатием соответствующего номера. Для ввода задачи ей необходимо дать имя, после чего на экране появляются характеристики задачи, которые следует конкретизировать. Например, дадим задаче имя “optimum”, после чего следует ответить на ряд вопросов (рис. 8).
| Max (1) или Min (2) целевой функции | <2> |
| Число основных переменных | <2> |
| Число ограничений | <3> |
| Приблизительный процент ненулевых решений (5% по умолчанию) | ENTER |
| Числа переменных (X1, X2,…,Xn) (1) | <1> |
| Использовать свободный формат при вводе данных | <0> |
| Использовать фиксированный формат | <1> |
Рисунок 8 – Подготовка задачи к вводу
Справа указаны цифры, соответствующие задаче: 
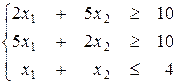
Целесообразно использовать фиксированный формат. Если все данные указаны, то следует нажать пробел. После этого появится шаблон для ввода коэффициентов и знаков неравенств. После ввода каждого элемента нажимают ENTER. Для продолжения работы нажимают ПРОБЕЛ и дважды ENTER, после чего возвращаются в Меню функции.
|
|
|
Если есть необходимость, то нажимают клавишу 4 – “Просмотр введенных данных” и получают Меню для работы с исходными данными (рис. 9).
| – | Ввод входных данных на экран | |
| – | Печать входных данных | |
| – | Сохранить входные данные в файле ASСП | |
| – | Просмотр в свободном формате | |
| – | Печать с свободном формате | |
| – | Сохранить с свободном формате | |
| – | Возврат в функциональное меню |
Рисунок 9 – Работа с исходными данными
Возвращаясь в функциональное меню, используют пункт 5 “Решение задачи”, в результате чего получают Меню решения проблемы (рис. 10).
| – | Решить без отображения таблиц | |
| – | Решить и отобразить начальную таблицу | |
| – | Решить и отобразить последнюю таблицу | |
| – | Решить и отобразить начальную и последнюю таблицы | |
| – | Решить и отобразить каждую таблицу | |
| – | Решить графическим методом | |
| – | Не использовать масштаб | |
| – | Возврат в функциональное меню |
Рисунок 10 – Меню решения проблемы
Если выбрать опцию 5 – “Решить и отобразить каждую таблицу”, то нажатием клавиши ENTER получают все последовательные операции, пока дойдут до оптимального решения. При этом вводимые в базис переменные и выводимые из него будут подсвечены. После финальной таблицы, нажав ПРОБЕЛ, оказываются в Меню просмотра последнего решения (рис. 11).
| – | Отобразить итоговый отчет | |
| – | Печатать итоговый отчет | |
| – | Отобразить решение | |
| – | Печатать решение | |
| – | Отобразить решение и анализ чувствительности | |
| – | Печатать решение и анализ чувствительности | |
| – | Печатать последнюю таблицу | |
| – | Сохранить последнее решение в файле ASСП | |
| – | Возврат к функциональному меню |
Рисунок 11 – Меню просмотра последнего решения
Для разных модулей Главного меню могут появиться несущественные особенности в определении решения и его анализе. В процессе диалога можно экспериментировать и выбрать интересующую пользователя опцию.
| 5. Л и т е р а т у р а |
1. Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высшая школа, 1986.
2. Басов А.С. Линейное программирование в технико-экономических задачах. - М: Наука, 1974.
|
|
|
3. Вентцель Е.С. Введение в исследование операций. - М.: Радио, 1984.
4. Гасс С. Линейное программирование. - М.: Физматгиз, 1971.
5. Гершгорн А.С. Математическое программирование и его применение в экономических расчетах. - М.: Экономика, 1978.
6. Дегтярев Ю.И. Исследование операций. - М.: Высшая школа, 1986.
7. Зайченко Ю.П. Исследование операций. - К.: Вища школа, 1988.
8. Карасев А.И. и др. Курс высшей математики для экономических вузов, ч. II. - М.: Высшая школа, 1983.
9. Карманов В.Г. Математическое программирование. - М.: Наука, 1980-
10. Кузнецов Ю.Н. и др. Математическое программирование. - М.: Высшая школа, 1980.
11. Ляшенко И.Н. и др. Линейное и нелинейное программирование. - К.: Вища школа, 1975.
12. Монахов В.М. Методы оптимизации. - М.: Просвещение. 1978.
13. Пенина Г.Г., Дрибан В.М. Математическое программирование (часть I). - Донецк, ДИП, 1996.
14. Полунин И.Ф. Курс математического программирования. - Минск.: Мир, 1970.
15. Щедрин Н.И., Кархов А.И. Математические методы программирования в экономике. - М.: Статистика, 1974.
16. Пенина Галина Геннадиевна – канд.экон.наук, доцент
Пенина Галина Геннадиевна – канд.экон.наук, доцент
|
|
|


