Дробно-линейное программирование

Если в задаче с линейными ограничениями задана дробно-линейная целевая функция, то такая задача мо­жет быть преобразована к традици­онному виду путем несложных пре­образований. Преобразованная модель может быть разрешена симплексным ме­тодом, а найденное решение трансформировано в решение ис­ходной задачи дробно-линейного программирования. Все этапы алгоритма проиллюстрируем на конкретном примере.

1. Систему ограничений приводят к каноническому виду:

где	─ основные переменные;
	─ дополнительные переменные;
	─ искусственные переменные.

2. Знаменатель целевой функции обозначают через , это приво­дит к следующему:

§ появится дополнительное ограничение или ;

§ функция цели приобретет вид .

3. Все ограничения умножают на 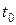и к ним добавляют дополни­тельное соотношение.

 

4. Вводят обозначения:

; ; ;

; ; ; .

Упорядочивают систему относительно новых переменных, перено­ся из правой части элементы, связанные с 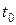. Кроме того, в допол­нительное ограничение вводят искусственную переменную со сле­дующим номером, в данном случае вводят . Это необходимо для формирования начального базиса. В результате указанных преоб­разований задача приобретает вид:

 

5. Задача приобрела каноническую форму, ее решение может быть выполнено симплексным методом. Учитывая, что индексы векторов должны соответствовать индексам переменных (, , и т.д.), вектор свободных членов обозна­чают через - это избавит от путаницы.

 

 

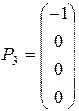
Таблица 1

Начальное симплекс-решение

 

Б	С											С.о.
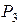
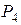
			-6			-1
			-14				-1
			-5
												1/5
-строка			-3	-2
-строка		-20			-1	-1

 

Данной таблице соответствуют такие значения переменных:

; ; ; ; ; ; ; ; .

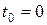Это решение не оптимально.

В таблице 1 получено три одинаковых симплексных отноше­ния, - все они равны нулю. При выборе ключевой строки руковод­ствуются правилом: берут ту, которая соответствует большему элементу ключевого столбца. В данном случае выбирают первую строку, и генеральный элемент равен 6.

Таблица 2

Вторая симплексная таблица

 

Б	С										С.о.
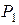
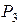
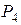
			-1	1/6		-1/6
			-12	40/6		2/6	-1
			-4	5/6		1/6
				19/6		5/6					6/19
-строка		-2	-16/6		-2/6
-строка		-7	59/6		7/6	-1

 

Второе решение выглядит так:

; ; ; ; ; ; ; ; .

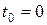Оно не оптимально.

Переход к третьей таблице выполняется по обычным правилам с учетом комментария к выбору ключевой строки, сделанного после таблицы 1.

Таблица 3

Третье симплексное решение

 

Б	С									С.о.
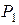
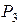
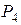
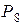
			-28/40			-7/40	1/40			-
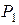
			-72/40			2/40	-6/40			-
			-100/40			5/40	5/40			-
			428/40			27/40	19/40			40/428
-строка		-272/40			-8/40	-16/40
-строка		428/40			27/40	19/40

 

Третье решение:

.

Условие оптимальности все еще не выполняется, переходят к следующей таблице.

Анализ показывает, что значения большинства переменных будут равны нулю до тех пор, пока ключевой строкой будет оставаться строка с нулевым элементом в . Как только ключевой станет строка с ненулевым эле­ментов в , так базисные переменные обретут конкретные зна­чения.

Таблица 4

Четвертое симплексное решение

 

Б	С								С.о.
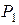
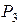
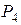
		28/428				-56/428	24/428		-
		72/428				70/428	-30/428		72/70
		100/428				121/428	101/428		100/121
		40/428				27/428	19/428		40/27
-строка	272/428				98/428	-42/428

 

Решение, соответствующее таблице 4, имеет вид:

, , , , .

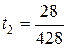Оно не является оптимальным, строят следующее симплекс-преобразование.

 

Таблица 5

Пятое симплексное решение

 

Б	С
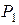
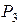
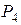
		21/121					20/121	56/121
		4/121					-25/121	-70/121
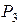
		100/121					101/121	428/121
		5/121					-1/121	-27/121
-строка	54/121					-35/121	-98/121

 

В таблице 5 получено решение, удовлетворяющее условию опти­мальности:

, , , , .

 

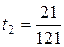6. Определяют значения исходных переменных:

Таким образом, решение задачи дробно-линейного программиро­вания будет следующим:

.

7. Дают, если возможно, геометрическую интерпретацию задачи:

§ находят область допустимых значений;

§ отмечают точки, соответствующие симплекс-таблицам.

 

Областью решений является треугольник . Первые ре­альные значения переменных появились в четвертой симплекс­ной таблице, им соответствуют такие значения исходных неизвестных: 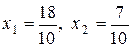. На графике – это вершина 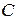, она оптимальной не является. Оптимальное решение обеспечивает верши­на .

 

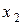
														А
																С					В
		-5		-4		-3		-2		-1
												-1

Замечание. Дробно-линейную задачу с двумя переменными можно решать графическим методом, основываясь на таких правилах:

1. По системе заданных ограничений строят область допустимых решений.

2. Выбирают произвольное значение 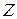и строят соответствующую прямую 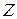– она обязательно пройдет через начало координат.

3. Обозначим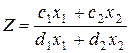

§ если , то, поворачивая прямую 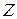против часовой стрелки до опорного положения, получим точку минимума (для получения максимума прямую поворачивают по часовой стрелке);

§ если 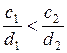, то для получения минимума прямую поворачивают по часовой стрелке до опорного положения (для максимума – против часовой стрелки).

4. Определив оптимальные точки, находят их координаты – это и будут оптимальные значения переменных, после чего вычисляют величину функции цели.

 

Пример. Найти решение дробно-линейной задачи.

, рассмотрим 2 варианта функции

а)

б)

 

1. Строим область допустимых решений – она определяется тремя неравенствами и представляем собой треугольник .

 

2. Строим прямую

а)

б)

; ;

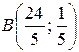а) ; ; ; ;

б) ; ; ; ;

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: