 |
Классическое определение вероятности события.
|
|
|
|
Преп. Т.Г. Макусева
Контрольная работа для студентов группы 5426, 28, 29 по дисциплине «Математика», задачи 1, 2, 3 и «Математика, ч. 2», задачи 1, 2, 3, 4.
Математика
Задача 1. Вычислить площадь плоской фигуры с помощью определенного интеграла. Сделать рисунок.
Пример решения задачи 4. 1) Вычислить площадь фигуры, ограниченной линиями 
, 
(рис. 8).
Решение. Площадь 
фигуры, ограниченной сверху и снизу непрерывными линиями 
и 
, пересекающимися в точках с абсциссами 
и 
, определяется по формуле
. (1)
Для нахождения точек пересечения данных линий решаем систему уравнений
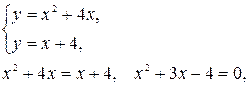
откуда 
. Применяя формулу (1), получим:
ЗАДАЧА 2. Составить уравнение прямой линии на плоскости. К задаче сделать рисунок.
1. Составить уравнение прямой, проходящей через точку М (-1, 2) параллельно вектору s (2, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
2. Составить уравнение прямой, проходящей через точку М (-3, 5) параллельно вектору s (1, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
3. Составить уравнение прямой, проходящей через точку М (6, 2) параллельно вектору s (0, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
4. Составить уравнение прямой, проходящей через точку М (1, 0) параллельно вектору s (-1, 2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
5. Составить уравнение прямой, проходящей через точку М (3, 5) параллельно вектору s (1, 0). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
6. Составить уравнение прямой, проходящей через точки М1 (3; 4), М2 (5; -1). Привести уравнение:
|
|
|
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
7. Составить уравнение прямой, проходящей через точки М1 (-1, 2), М2 (0, 2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
8. Составить уравнение прямой, проходящей через точки М1 (0, -1), М2 (3, -2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
9. Составить уравнение прямой, проходящей через точки М1 (2, 3), М2 (-2, 2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
10. Составить уравнение прямой, проходящей через точки М1 (6, 1), М2 (4, 2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
11. Составить уравнение прямой, проходящей через точку М (-1, 2) параллельно вектору s (2, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
12. Составить уравнение прямой, проходящей через точку М (-3, 5) параллельно вектору s (1, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
13. Составить уравнение прямой, проходящей через точку М (6, 2) параллельно вектору s (0, 1). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
14. Составить уравнение прямой, проходящей через точку М (1, 0) параллельно вектору s (-1, 2). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
15. Составить уравнение прямой, проходящей через точку М (3, 5) параллельно вектору s (1, 0). Привести уравнение:
а) к каноническому; б) параметрическому виду; в) к уравнению в отрезках.
ЗАДАЧА 3. Найти расстояние от точки А (х;у) до прямой
(уравнение прямой взять из задачи 2).
Координаты точки (x, y) вычисляются по формуле:
x=2k – 5, y = 3k – 10, где k – номер варианта контрольной работы.
|
|
|
Пример решения задачи 2-3.
1) Составить параметрическое и каноническое уравнения прямой, проходящей через точку М (3; -1) параллельно вектору s (2; 3).
Решение. Параметрическое уравнение прямой, проходящей через точку М (х 0; y 0) параллельно вектору s (m; n):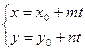 
.
Подставляя в формулу координаты данной точки М и вектора s, получаем: 
.
Каноническое уравнение прямой, проходящей через точку М (х0;y0) параллельно вектору s (m; n): 
.
Тогда каноническое уравнение прямой, проходящей через точку М (3;-1) параллельно вектору s (2; 3): 
.
Ответ: Параметрическое уравнение искомой прямой , каноническое .
2). Составить уравнение прямой в отрезках, проходящей через точки А (5; 4) и В (2; -3).
Решение. Уравнение прямой, проходящей через две точки М1(х1;y1) и М2(х2;y2) имеет вид: 
.
Уравнение прямой в отрезках: 
, где a и b – отрезки, которые отсекает данная прямая на осях Ох и Оу.
Составим сначала уравнение прямой, проходящей через данные точки:
Þ 
Þ 3(у + 3) = 7(х – 2) Þ 7х – 3y = 5.
Разделим полученное уравнение на 5: 
.
Ответ: уравнение прямой в отрезках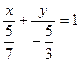 
.
3). Найти расстояние от точки М(-1; 4) до прямой 7х – 3y – 5 = 0.
Решение. Расстояние от точки М (х 0; у 0) до прямой Ах + Ву + С = 0 вычисляется по формуле: d = 
.
Т.о. расстояние от точки М(-1; 4) до прямой 7х – 3y – 5 = 0:
d =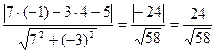 
.
Ответ: 
.
Математика, ч. 2.
Краткие теоретические сведения:
Классическое определение вероятности события.
За вероятность события А принимается отношение числа благоприятствующих этому событию элементарных исходов (m) к общему числу возможных исходов (n):
Если составляются такие комбинации из n элементов по m, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из n элементов по m определяется по формуле
Если комбинации отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится по формуле
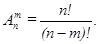
Если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно
|
|
|
