 |
Теоремы сложения и умножения вероятностей.
|
|
|
|
Теорема сложения вероятностей несовместных событий. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Сумма вероятностей событий, образующих полную группу, равна единице.
Теорема умножения вероятностей двух событий. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго относительно первого:
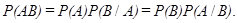
Данная теорема обобщается на любое конечное число событий.
Для независимых событий вероятность их произведения равна произведению вероятностей этих событий. Для двух независимых событий
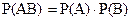
Теорема сложения вероятностей двух совместных событий. Вероятность сложения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Формула полной вероятности и формула Байеса.
Если некоторое событие В совершается с одним из n несовместных событий А1, А2, …Аn, образующих полную группу событий, то для определения вероятности этого события может быть использована формула полной вероятности
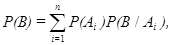
где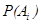 
- вероятность события 
; 
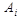условная вероятность события В.
Для определения вероятности события 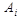при условии, что произошло событие В, используется формула Байеса
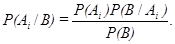
Формулы Бернулли и Пуассона.
Формула Бернулли определяет вероятность появления ровно m раз события А в серии из n независимых испытаний, в каждом из которых вероятность появления события А равна p:
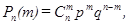
где
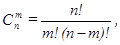
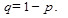
В некоторых случаях требуется определить вероятность появления события А менее m раз (X<m), более m раз (X>m), не менее m раз (X 
m), не более m раз (x m). В этих случаях могут быть использованы формулы
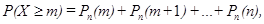
При больших n и малых p вычисления по формуле Бернулли затруднены. В этих случаях обычно используется формула Пуассона
|
|
|
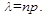
Обратите внимание, что есть еще шестая задача, она приведена в конце.
ВАРИАНТ I
Классическое определение вероятности события.
В магазин поступило 30 холодильников, пять из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность того, что он будет без дефекта?
Теоремы сложения и умножения вероятностей.
Вероятность попадания первым стрелком в мишень равно 0,3, вторым - 0,6, третьим – 0,5. Найти вероятность попадания в мишень двумя стрелками.
Формула полной вероятности и формула Байеса.
На предприятии, изготавливающем замки, первый цех производит 25, второй 35, третий 40% всех замков. Брак составляет соответственно 5, 4 и 2%.
а) Найти вероятность того, что случайно выбранный замок является дефектным.
б) Случайно выбранный замок является дефектным. Какова вероятность того, что он был изготовлен в первом, втором, третьем цехе?
Формулы Бернулли и Пуассона.
В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:
а) одного мальчика;
б) двух мальчиков.
ВАРИАНТ 2
Классическое определение вероятности события.
В коробке находится шесть одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки. Какова вероятность того, что сверла извлекутся в порядке возрастания их диаметра?
Теоремы сложения и умножения вероятностей.
Вероятность правильного оформления счета на предприятии составляет 0,95. Во время аудиторской проверки были взяты два счета. Какова вероятность того, что только один из них оформлен правильно?
|
|
|
