 |
Сложение гармонических колебаний одного направления и одинаковой частоты.
|
|
|
|
В этом случае результирующее колебание также является гармоническим. При этом амплитуда и фаза колебания определяются следующим образом:
амплитуда результирующего колебания
;
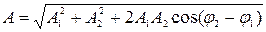начальная фаза результирующего колебания
,
где А 1, φ 1 и А 2, φ 2 – амплитуды и фазы складываемых колебаний.
Траектория точки, участвующей в двух взаимно-перпендикулярных колебаниях x = A 1cos ωt; y = A 2cos (ωt + φ), описывается уравнениями:
, если разность фаз φ = 0;
, если разность фаз φ = 
π;
, если разность фаз φ = 
.
Волновой процесс (волна) – это процесс распространения колебаний в пространстве.
Уравнение плоской (бегущей) синусоидальной волны имеет вид:
или 
,
где S (x, t) – мгновенное значение смещения любой точки среды от ее положения равновесия;
х – расстояние от источника волны до рассматриваемой точки;
υ – скорость распространения волны в среде;
k – волновое число, 
; λ – длина волны;
– фаза колебания точки среды.
Разность фаз Δφ колебаний двух точек волны, находящихся друг от друга на расстоянии Δ x, отсчитанном в направлении распространения волны, определяется как
,
где λ – длина волны.
Наложение когерентных волн.
Когерентными называются волны с постоянной во времени разностью фаз.
Когерентными являются гармонические волны с одинаковыми частотами (длинами волн).
При наложении когерентных волн в одних точках пространства они взаимно усиливают, а в других ослабляют друг друга. То есть происходит перераспределение энергии волн в пространстве. Это явление называется интерференцией волн.
Результат наложения волн зависит от разности их хода Δх, с которой они приходят в данную точку.
|
|
|
Условие усиления волн.
Если разность хода равна
, m = 0, 1, 2,
то в точку наложения волны приходят с одинаковыми фазами и усиливают друг друга. Величина m называется номером максимума.
Условие ослабления волн.
Если разность хода равна
, m = 0, 1, 2,
то в точку наложения волны приходят с противоположными фазами и ослабляют друг друга. Величина m называется номером минимума.
Примеры решения задач
Пример 15. Частица массой m = 0,01 кг совершает гармонические колебания с периодом T = 2 с. Полная энергия колеблющейся частицы E = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F max, действующей на частицу.
Решение
Для определения амплитуды колебаний воспользуемся выражением для полной энергии частицы
E = 1/2· m · ω 2· A 2,
где ω = 2π/ T.
Отсюда для амплитуды получим
A = 
.
Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = – k x, где k – коэффициент квазиупругой силы; x – смещение колеблющейся точки. Сила будет максимальной при максимальном смещении x max, равном амплитуде:
F max = kA.
Коэффициент k выразим через период колебаний:
k = m ω2 = 4π2 m / T 2.
Подставив выражения для полной энергии и коэффициента k в формулу для амплитуды и произведя упрощения, получим
.
Проведем анализ размерности:
.
Произведем вычисления:
A = 
= 0,045 (м) = 45 мм;
F max = 
= 4,44·10-3 (Н) = 4,44 мН.
Пример 16. Платформа совершает гармонические колебания в горизонтальной плоскости с частотой 2 Гц и амплитудой 1 см. На платформе лежит груз, коэффициент трения которого о платформу 0,2. Будет ли груз скользить по платформе? Ответ обосновать.
Решение
Для решения приведем рисунок 13.
Груз будет скользить в том случае, когда максимальная сила инерции m · amax, действующая на груз будет равна или больше силы трения F тр. В рассматриваемом случае сила трения
|
|
|
F тр = µ · m · g, (34)
где m – масса груза;
g – ускорение свободного падения.
Максимальное ускорение силы инерции amax равно максимальному ускорению колеблющейся платформы, которое определяется как
amax = ω 2 · А или amax = 4π2 · ν 2 · А.
Произведение amax и массы груза дает максимальную силу инерции:
F ин = m · 4 π 2 · ν 2 · А. (35)
Приравняв (34) и (35) и выразив ν, получим формулу для частоты, при которой груз будет скользить по платформе
.
Произведем вычисления:
.
Согласно условию груз будет скользить при значении частоты, равном полученному значению или больше него. Так как заданное значение частоты меньше полученного, то груз не будет скользить по платформе.
Пример 17. В колебательном контуре происходят свободные колебания. Зная, что максимальный заряд конденсатора 10-6 Кл, а максимальная сила тока 10 А, найти частоту колебаний этого контура.
Решение
При электрических колебаниях кинематическое уравнение колебания заряда записывается в виде
,
где ω – циклическая частота колебания;
φ 0 – начальная фаза колебания.
Взяв производную по времени от заряда, получим уравнение колебания силы тока
. (36)
В уравнении (36) произведение максимального заряда и циклической частоты определяет максимальное (амплитудное) значение силы тока:
. (37)
При известных значениях q max и I max можно найти циклическую частоту. По условию задачи требуется найти ν. Поэтому используем формулу, которая связывает ω и ν:
ω = 2π · ν. (38)
Подставив (38) в (37) и выразив ν, получим расчетную формулу
.
Произведем расчеты:
.
Пример 18. Напряжение и сила тока в катушке изменяются по законам U (t) = 60sin(314 t + 0,25 π)и i (t) = 15·sin(314· t).
Определить разность фаз Δφ между током и напряжением, а также полное Z, активное R и реактивное X p сопротивления катушки.
Решение
Известно, что фазой колебания называется величина, стоящая под знаком sin или cos. Поэтому искомая разность фаз Δφ определяется, как разность
Δ φ = (314· t +0,25 π) – 314· t = 0,25 π.
Полное сопротивление определим с помощью законf Ома для цепи переменного тока
|
|
|
,
где U a и I a – амплитудные значения напряжения и силы тока.
Из заданных уравнений следует, что U a = 60 В и I a = 15 А. Следовательно, полное сопротивление
.
Для определения активного R и реактивного 
сопротивлений запишем формулы для полного сопротивления
(39)
и для сдвига фаз
, (40)
где L – индуктивность катушки.
Выразив ω · L из (40) и подставив в (39), получим формулу для активного сопротивления
.
Подставив в эту формулу найденные значения Z и Δ φ рассчитаем R:
.
Теперь по формуле (39) можно найти Х р
.
Таким образом, получили, что при такой разности фаз R = X p.
Пример 19. Синусоидальная волна распространяется вдоль упругого шнура со скоростью 15м/с. Период колебания точек шнура 2,4 с, а амплитуда колебания 7 см. Определить длину волны, фазу и смещение точки, отстоящей на 45 м от источника колебаний, через 4 с.
Решение
Уравнение синусоидальной волны имеет вид:
, (41)
где ω – циклическая частота;
k – волновое число;
ω·t – k·x =Ф – фаза колебаний.
Выразим ω и k через заданные величины:
и 
.
Тогда формула фазы примет вид
. (42)
Определим длину волны λ:
λ = υ ·Т = 15 · 2,4 = 36 м
и фазу волны:
.
Теперь, подставив это значение фазы в формулу (41), определим искомое смещение:
S (x,t) = 7 · 10-2 · sin(5π/6) = 3,5 · 10-2 м.
Пример 20. Два когерентных источника колеблются в одинаковых фазах с частотой 300 Гц. Скорость распространения колебаний в среде равна 1,5 км/с. Определить, при какой наименьшей разности хода волн будет наблюдаться максимальное ослабление колебаний. Каков результат интерференции в точке, расположенной на расстоянии 20 м от первого источника и 30 м от второго?
Решение
Для решения задачи используем условие усиления
(43)
и ослабления когерентных волн при их наложении
, (44)
где m = 0, 1, 2,
λ – длина волны.
Найдем искомую разность хода.
Из (44) следует, что волны будут ослаблять друг друга, если в точку наложения они приходят с разностью хода Δх, равной нечетному числу полуволн. Минимальной разности хода соответствует m = 0.
|
|
|
Поэтому
. (45)
По известной формуле найдем длину волн:
λ = υ· Т = υ / ν = 1500/300 = 5 м.
По формуле (44) для ∆х min получим
∆ х min = 5/2 = 2,5 м.
Найдем результат наложения волн в заданной точке, для которой разность хода равна х 2 – х 1 = 30 – 20 =10 м.
Из формул (43) и (44) видно, что результат наложения волн зависит от того, четному или нечетному числу λ /2 равна разность хода.
Поделив заданную разность хода на λ /2, получим
.
Число полуволн получилось четным. Это значит, что в заданной точке будет происходить усиление волн.
Список литературы
1. Трофимова, Т.И. Курс физики: Учебное пособие для втузов / Т.И. Трофимова – М.: Изд. «Академия», 2007.– 560с.
2. Детлаф А.А, Яворский Б.М. Курс физики. – М.: Высшая школа. 2001. – 718с.
3. Трофимова, Т.И. Курс физики. Задачи и решения. Учебное пособие для втузов/Т.И. Трофимова, А.В. Фирсов.– М.: Изд. «Академия», 2004.–592с.
4. Волькенштейн, B.C. Сборник задач по общему курсу физики.– М.: Изд. «Наука», 2003.– 328с.
5. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высш. шк. 1981.– 430с.
6. Сена, Л.А. Единицы физических величин и их размерность. – М.: Наука, 1988.– 432 с.
Приложение А
(справочное)
|
|
|
