 |
Орбиты группы перестановок
|
|
|
|
Связь комбинаторики с различными разделами математики
Выполнила:
студентка V курса математического факультета
Бородулина Юлия Анатольевна
Научный руководитель:
к. ф-м. н., доцент кафедры алгебры и геометрии
Е.М. Ковязина
Рецензент:
к. ф-м. н., доцент кафедры алгебры и геометрии
О.С. Руденко
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой Е.М. Вечтомов
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение........................................................................................................... 3
§1. Применение леммы Бернсайда к решению комбинаторных задач......... 5
1.1. Орбиты группы перестановок.......................................................... 5
1.2. Длина орбиты группы перестановок. Лемма Бернсайда................ 5
1.3. Комбинаторные задачи.................................................................... 8
§2. «Метод просеивания».............................................................................. 21
2.1. Формула включения и исключения................................................ 21
2.2. Общий «метод просеивания» или «пропускания через решето». Решето Сильва-Сильвестра........................................................................................ 23
2.3. Использование общего метода решета в теории чисел................. 23
§3. Разбиение фигур на части меньшего диаметра...................................... 28
§4. «Счастливые билеты».............................................................................. 34
Библиографический список........................................................................... 39
Введение
Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов называется комбинаторикой. Комбинаторика возникла в XVI веке. Вопросы, касающиеся азартных игр, явились движущей силой в развитии комбинаторики. Сейчас комбинаторные методы применяются как в самой математике, так и вне её – теория кодирования, планирование эксперимента, топология, конечная алгебра, математическая логика, теория игр, кристаллография, биология, статистическая физика, экономика и т.д.
|
|
|
Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования.
Цель дипломной работы: показать связь комбинаторики с различными разделами математики.
Задачи:
1. Изучить лемму Бернсайда и решить комбинаторные задачи о раскраске с её применением;
2. Показать применение метода «просеивания» для подсчёта количества простых и взаимно простых чисел;
3. Рассмотреть теорему Борсука, которая решает задачу для плоских фигур о разбиении их на части меньшего диаметра;
4. Решить задачу о «счастливых билетах».
Дипломная работа состоит из четырёх частей:
В § 1 рассмотрена связь теории групп с комбинаторикой: применение группы перестановок к решению комбинаторных задач. Основной используемый факт в этом параграфе – лемма Бернсайда.
В § 2 показан наиболее общий метод пересчёта (известный ещё в XVIII веке), а также приведены примеры его использования в теории чисел.
Параграф 3 посвящён вопросу комбинаторной геометрии – вопросу о разбиении фигуры на несколько меньших частей. Рассмотренная теорема Борсука является тем стержнем, вокруг которого возможно дальнейшее рассмотрение этого вопроса.
В § 4 решается известная задача о счастливых билетах с привлечением методов из математического анализа.
§ 1. Применение леммы Бернсайда к решению комбинаторных задач [3]
|
|
|
Орбиты группы перестановок
Пусть G – группа перестановок на множестве М={1, 2, …, n }. Подмножество О 
М называется орбитой группы G, если: а) α(a) 
O для любого α G и любого a O, то есть действие перестановок из G на элементы О не выводит за пределы О; б) любые два элемента из О можно перевести друг в друга некоторой перестановкой из G.
Легко показать, что всякая группа перестановок G ={ ε = α 0, α 1, …, αk -1 } имеет орбиты.
Орбитами подобного вида исчерпываются все типы орбит, то есть, если О – орбита группы G и а О, то О=О(а).
Любые две орбиты О(а) и О(b) либо совпадают (если b 
O (a)), либо не пересекаются (если b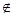 
O (a)).
Таким образом, множество М распадается в объединение непересекающихся подмножеств – орбит группы G. В связи с разбиением множества М на орбиты группы перестановок G возникают следующие два вопроса:
1) Сколько орбит имеет группа G на множестве М?
2) Какова длина каждой из этих орбит, то есть из скольких элементов они состоят?
Ответим на эти вопросы.
|
|
|
