 |
Использование общего метода решета в теории чисел
|
|
|
|
Теорема 1. Пусть А={1, 2, …, n } и а1, а2, …, а r, 
, i =1, 2, …, r, попарно взаимно просты. Количество целых чисел k таких, что 0 < k ≤ n, ai не делит k, i =1, 2, …, r, равно
(8)
Доказательство. Обозначим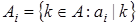 
и выпишем формулу (2):
(9)
Имеем
Card A=n,
Card Ai= 
, i=1, 2, …,r,
, i≠j, i, j=1, 2, …,r,
∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ (10)
= 
.
Подставляя (10) в (9), получаем (8).
Пример. Пусть 
, а1=3, а2=7, а3=8.
Количество целых чисел, не превосходящих 35 и не делящихся ни на 3, ни на 7, ни на 8, равно
Рассмотрим другие приложения.
Количество целых чисел k таких, что
0 < k ≤ n, (k, n)=1, 
,
обозначают через φ (n) и называют функцией Эйлера.
Теорема 2. Пусть . Тогда
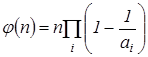, (11)
где произведение берётся по всем простым делителям а i числа n.
Доказательство. Так как все ai делят n и взаимно просты, то имеем
= 
.
По формуле (8)
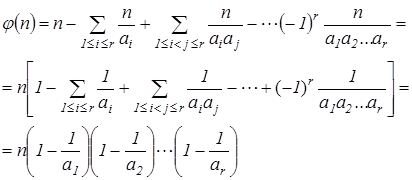
т.е. получаем (11).
Пример. Пусть n =84. Простыми делителями 84 являются 2, 3, 7; поэтому
Функция Мёбиуса. Представим (11) в другом виде, используя функцию Мёбиуса μ(n), определяемую следующим образом:
μ(1) = 1;
μ(n) = 0, если n делится на квадрат простого числа;
μ(а1а2…а r)=(-1) r, если ai – различные простые множители, i =1, 2, …, r.
Преобразуем равенство (11), используя функцию Мёбиуса:
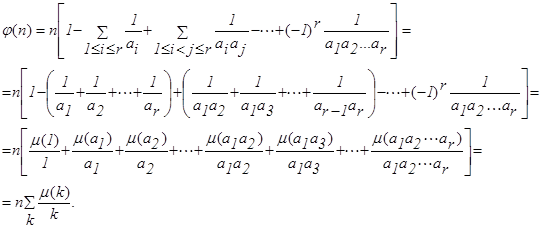
Тогда
, (12)
где суммирование производится по всем k, делящим n (включая 1).
Пример. Имеем
μ(1) =1, 
, 
,
, 
,
, 
,
, 
,
, 
, 
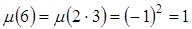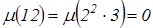При n =84 формула (12) даёт
|
|
|
Решето Эратосфена. Известен следующий способ перечисления простых чисел pi, pi ≤ n: вычисляется 
и из последовательности 2, 3, …, n вычеркиваются последовательно все числа, кратные 2, затем кратные 3, …, кратные c. Оставшиеся числа и есть искомые.
Используя теорему 2, можно получить следующую формулу пересчёта. Если через M (n) обозначить количество простых чисел q таких, что 
, то в силу (8)
M (n)= 
(13)
где pi -, i =1, 2, …, r, - простые числа, не превосходящие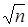 
(- 1 в правой части добавляется, так как 1 не считается простым).
В силу (12)
M (n)= 
, (14)
где суммирование в (14) производится по всем простым делителям n (включая 1).
Пример. Сколько простых среди чисел 2, 3, …, 84? Имеем 
=9. Простыми числами между 2 и 9 будут 2, 3, 5, 7. Согласно (13)
Таким образом, имеется всего 19 + 4 = 23 простых числа среди 2, 3, …, 84. Решето Эратосфена перечисляет их: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83.
Расширения данной темы: иногда подмножества не выделяются, а фиксируется число свойств, которыми обладают их элементы. Для этого случая можно вывести формулу, используя формулу (6).
§3. Разбиение фигур на части меньшего диаметра [1, 2]
Диаметром фигуры F назовём такое расстояние d, что, во-первых, расстояние между любыми двумя точками M и N фигуры F не превосходит d, и, во-вторых, можно отыскать в фигуре F хотя бы одну пару точек A, B, расстояние между которыми в точности равно d.
Примеры:
· Если фигура F представляет собой сегмент круга, ограниченный дугой l и хордой а, то в случае, когда дуга l не превосходит полуокружности, диаметр фигуры F равен а; в случае же, когда дуга l больше полуокружности, диаметр фигуры F совпадает с диаметром всего круга.
· Если фигура F представляет собой многоугольник, то его диаметром является наибольшее из расстояний между вершинами.
В фигуре может существовать и много пар точек, расстояние между которыми равно d: в случае эллипса такая пара точек только одна, в случае квадрата их две, в случае правильного треугольника – три, в случае круга таких пар бесконечно много.
|
|
|
Постановка задачи: Круг диаметра d нельзя разбить на две части, диаметр каждой из которых будет меньше d, но можно разбить на три такие части (рис. 4(а, б)).
Тем же свойством обладает равносторонний треугольник со стороной d. Но имеются фигуры, которые можно разбить на две части меньшего диаметра (рис. 5(а, б)).
Мы можем рассматривать для любой фигуры F задачу о разбиении её на части меньшего диаметра. Наименьшее число частей, которые для этого потребуются, обозначим через a (F). Если F – круг или равносторонний треугольник, то a (F) = 3, а для эллипса или параллелограмма a (F) = 2. Возникает вопрос, нельзя ли найти плоскую фигуру, для которой a (F)>3, то есть такую фигуру, что для разбиения её на части меньшего диаметра нельзя обойтись тремя частями, а потребуется 4 или большее число частей?
Ответ даёт т еорема Борсука: Всякая плоская фигура F диаметра d может быть разбита на три части диаметра меньше d, то есть a (F) ≤ 3.
Лемма: Всякая плоская фигура диаметра d может быть заключена в правильный шестиугольник, у которого расстояние между параллельными сторонами равно d.
Доказательство леммы.
Проведём к фигуре F опорные прямые l 1 и l 2, причём l 2 параллельна l 1. Вся фигура будет находиться в полосе между прямыми l 1 и l 2, расстояние между которыми не превосходит d (так как диаметр фигуры F равен d) (рис. 6). Проведём к фигуре F две параллельные опорные прямые m 1 и m 2, составляющие с l 1 угол 60°. Прямые l 1, l 2, m 1, m 2 образуют параллелограмм ABCD с углом 60° и высотами не превосходящими d, внутри которого целиком заключается фигура F. Проведём две опорные прямые p 1, p 2 фигуры F, составляющие с l 1 угол 120°, и обозначим через M и N основания перпендикуляров, опущенных на эти прямые из концов диагонали AC параллелограмма (рис. 6). Покажем, что направление прямой l 1 можно выбрать таким образом, чтобы выполнялось равенство AM = CN. Допустим, AM ≠ CN, и пусть, для определённости, AM < CN. Таким образом, величина y = AM – CN отрицательна. Начнём непрерывно изменять направление прямой l 1 так, чтобы она повернулась на 180° (фигуру F будем оставлять неподвижной). Вместе с прямой l 1 будут менять своё положение прямые l 2, m 1, m 2, p 1, p 2 (так как их положение определяется выбором l 1). Поэтому при повороте прямой l 1 будут непрерывно перемещаться и точки A, C, M, N, а значит, будет не 
прерывно изменяться величина y = AM – CN.
|
|
|
Но когда прямая l 1 повернётся на 180°, она займет положение, которое раньше занимала прямая l 2. Поэтому мы получим тот же параллелограмм, что и на рис. 6, но в нем точки А и С, а так же М и N поменяются «ролями». Следовательно, в этом положении величина у будет уже положительной.
Если мы теперь изобразим график изменения величины у при повороте прямой l 1 от 0° до 180° (рис. 7), то увидим, что найдётся положение прямой l 1, при котором величина у обращается в нуль, т.е. АМ = CN (ибо, непрерывно изменяясь от отрицательного значения до положительного, величина у должна в некоторый момент обратиться в нуль). Мы рассмотрим положение всех наших прямых как раз в тот момент времени, когда величина у обращается в нуль (рис. 8). Из равенства АМ = CN вытекает, что шестиугольник, образованный прямыми l 1, l 2, m 1, m 2, p 1, p 2, центрально-симметричен.
Каждый угол этого шестиугольника равен 120°, а расстояние между противоположными сторонами не превосходит d. Если расстояние между p 1 и p 2 меньше d, то мы раздвинем эти прямые (перемещая их на одинаковое расстояние) так, чтобы расстояние между раздвинутыми прямыми было равно d. Точно так же мы поступим с прямыми l 1, l 2, а за тем с прямыми m 1, m 2. В результате мы получим центрально-симметричный шестиугольник (с углами 120°), у которого противоположные стороны удалены друг от друга на расстояние d. Из сказанного ясно, что все стороны этого шестиугольника равны между собой, т. е. этот шестиугольник – правильный, причём фигура F расположена внутри шестиугольника.
Доказательство теоремы Борсука. Пусть F – фигура диаметра d. Согласно доказательной лемме, фигура F содержится внутри правильного шестиугольника, расстояние между противоположными сторонами которого равно d. Покажем, что этот правильный шестиугольник можно разрезать на три части, каждая из которых имеет диаметр, меньший d. При этом фигура F также разрежется на три части, диаметр каждой из которых будет меньше d. Требуемое разбиение правильного шестиугольника на три части показано на рис. 9 (точки P, Q и R являются серединами сторон, а О – центр шестиугольника). Чтобы убедится, что диаметры частей меньше d, достаточно заметить, что в треугольнике PQL угол Q прямой, и поэтому PQ < PL = d. Таким образом, теорема доказана.
|
|
|
Из доказательства теоремы легко заключить, что всякая плоская фигура диаметра d может быть разбита на три части, диаметр каждой из которых не превосходит 
(так как PQ = 
) (рис. 9). Эта оценка диаметров частей является наилучшей, так как круг диаметра d нельзя разбить на три части, диаметр каждой из которых был бы меньше (часть, имеющая диаметр меньше 
, высекает на окружности множество, расположенное на дуге, меньшей 120°, поэтому три такие части не покрывают всей окружности).
Можно предложить следующие расширения по данному вопросу:
Теорема Борсука является стержнем этого вопроса, но она не даёт полного решения вопроса о том, чему равно a (F) для произвольной заданной фигуры F диаметра d. Она даёт лишь оценку a (F) сверху: a (F) ≤ 3. В то же время, очевидно, что a (F) ≥ 2 для любой фигуры. Возникает задача: для каких плоских фигур a (F) равно двум и для каких оно равно трём.
Можно рассматривать задачу о покрытии выпуклых фигур гомотетичными (о наименьшем числе «уменьшенных копий» фигуры F, которыми можно покрыть всю фигуру F) и задачу о наименьшем числе направлений, освещающих всю границу фигуры F.
Все эти задачи можно рассмотреть для пространственных тел.
§4. «Счастливые билеты» [5]
Назовём билет счастливым, если сумма первых трёх цифр его номера равняется сумме последних трёх цифр (для шестизначных номеров). Возникает вопрос, сколько всего существует счастливых билетов?
Разобьём все счастливые билеты на классы, в каждом из которых сумма первых трёх цифр одинакова. Эта сумма может принимать значения от 0 (для тройки цифр 000) до 27 (для тройки 999). Поэтому число классов равно 28. Обозначим через an число различных троек цифр с суммой цифр n. Первые несколько значений an нетрудно вычислить:
· а0 = 1 (есть всего одна тройка цифр 000 с суммой 0);
· а1 = 3 (есть три тройки 001, 010, 100 с суммой цифр 1);
· а2 = 6 (тройки 002, 020, 200, 011, 101, 110).
Число счастливых билетов, сумма первых трёх цифр которых равна n, есть an 2 (как в начале, так и в конце номера счастливого билета можно поставить любую тройку цифр с суммой n). Таким образом, для подсчёта числа счастливых билетов нам достаточно вычислить числа an, а затем найти сумму квадратов этих 28 чисел.
|
|
|
Для вычисления значений an посчитаем число одно- и двухзначных чисел с суммой цифр n. Для каждого n = 0, 1, 2, …,9 существует ровно одно однозначное число с суммой цифр n (запись этого числа совпадает с записью числа n). Будем описывать однозначные числа многочленом 
. Смысл у этого многочлена следующий: коэффициент при sn в многочлене А1 равен числу однозначных чисел, сумма цифр которых равна n. Другими словами, коэффициент при sn в многочлене А1 равен 1, если 0≤ n ≤9, и равен 0, если n >9.
Выпишем многочлен А2(s), описывающий двузначные числа. Коэффициент при sn в многочлене А2(s) равен числу двузначных чисел с суммой цифр n. (Мы рассматриваем и такие двузначные числа, в которых первая цифра или обе цифры могут равняться нулю). Степень многочлена А2 равна 18 (это наибольшая возможная сумма цифр двузначного числа): 
.
Предложение 1. А2(s) = (А1(s))2.
Доказательство. Произведение мономов sk и sm даёт вклад в коэффициент при мономе sn многочлена (А1(s))2 в том и только в том случае, если n = k + m. Поэтому коэффициент при мономе sn в многочлене (А1(s))2 есть в точности число способов представить число n в виде суммы n = k + m, k, m = 0, 1,..., 9. Таким образом, многочлен в правой части равенства совпадает с многочленом А2.
Выпишем многочлен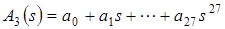 
.
Предложение 2. А3(s) = (А1(s))3.
Доказательство. Коэффициент при мономе sn в многочлене (А1(s))3 равен числу представлений числа n в виде суммы трёх цифр n = k + m + l, k, m, l = 0, 1,..., 9.
Итак, задача о числе счастливых билетов свелась к следующему: надо посчитать число р0 – сумму квадратов коэффициентов многочлена (А1(s))3. Умножение на многочлен А1(s) – очень простая операция. Но мы применим аппарат математического анализа.
Подставим вместо s выражение eiφ. Тогда А3(eiφ) = (А1(eiφ))3 будет тригонометрическим полиномом 27-й степени:
.
Воспользовавшись тем, что
, получим
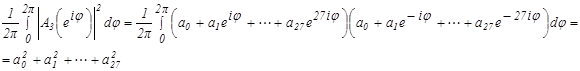
Суммируя геометрическую прогрессию и пользуясь тем, что 
,
получаем 
, откуда искомая величина равна
. (15)
Попробуем оценить значение интеграла (15). График функции 
на отрезке 
выглядит так:
В нуле функция достигает своего максимума, равного 10. Вне отрезка 
величина функции f не превосходит 
. Поэтому вклад дополнения к отрезку 
в интеграл (1) не превосходит π∙36≈2100 (на самом деле он значительно меньше). Основная же составляющая интеграла (1) сосредоточена на отрезке 
. Для оценки вклада этого отрезка воспользуемся методом стационарной фазы. Этот метод позволяет оценить значение интеграла 
при t → ∞. При больших значениях t величина интеграла определяется поведением функции ln f («фазы») в окрестности своей стационарной точки 0 (точки, в которой (ln f)′ = 0, или, что то же самое, f ′ = 0). В окрестности нуля 
, а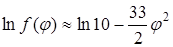 
.
При больших t имеем
.
Полагая t = 6 и пользуясь формулой (15), получаем приближённое равенство 
. Полученный результат с хорошей точностью (отклонение составляет не более 3%) приближает искомое значение.
На основании рассмотренного примера можно сделать некоторые выводы о комбинаторных задачах и методах их решения. Задачи перечислительной комбинаторики состоят в подсчёте числа объектов, принадлежащих некоторому семейству конечных множеств. У каждого множества семейства имеется свой номер (в задаче о счастливых билетах таким номером была сумма цифр трёхзначного числа).
Как правило, задача перечислительной комбинаторики «в принципе» разрешима: для каждого множества из семейства можно выписать все его элементы и таким образом узнать их число. Проблема состоит в том, чтобы найти «хорошее» решение, не требующее выписывания всех элементов изучаемых множеств. Определить, что такое «хорошее» решение, довольно трудно.
При решении задач перечислительной комбинаторики очень полезно рассматривать производящие многочлены. В нашем случае пользу принёс производящий многочлен А3. Операции с комбинаторными объектами очень естественно выражаются в терминах производящих функций. Так, переход от однозначных чисел с заданной суммой цифр к трёхзначным числам состоял просто в возведении производящего многочлена А1 в куб. Привлечение методов из смежных областей математики (например, из анализа) позволяет по-иному взглянуть на перечислительную задачу и найти новые, зачастую неожиданные, подходы к её решению.
Библиографический список
1. Болтянский, В.Г. Теоремы и задачи комбинаторной геометрии [Текст] / В.Г. Болтянский, И.Ц. Гохберг // – М.: Наука, 1965.
2. Болтянский, В.Г. Разбиение фигур на меньшие части [Текст] / В.Г. Болтянский, И.Ц. Гохберг // – М.: Наука, 1971.
3. Калужнин, Л.А. Преобразования и перестановки [Текст] / Л.А. Калужнин, В.И. Сущанский // – М.: Наука, 1979.
4. Кофман, А. Развитие методов пересчета [Текст] / А. Кофман // Введение в прикладную комбинаторику – М.: Наука, 1975. – с. 60–73.
5. Ландо, С.К. Счастливые билеты [Текст] // Математическое просвещение, сер. 3, вып. 2. – М.: Просвещение, 1998. – с. 127–132.
|
|
|
