Длина орбиты группы перестановок. Лемма Бернсайда

Ответим на второй вопрос. Для любого элемента а М можно рассмотреть группу G_a всех перестановок из G, для которых точка а является неподвижной. Она называется стабилизатором точки а. Ответим на вопрос, доказав следующую теорему:

Длина орбиты О(а) равна индексу стабилизатора G_a в группе G, то есть | O (a)|= | G |:| G_a |.

Доказательство. Пусть G ={ ε = α ₀, α ₁, …, α_{k -1} }, G_a ={ε=β₀, β₁, …, β _{s -1} }. Для подсчёта различных элементов в последовательности a =α₀(a), α₁(a), …, α _{k -1} (a) удобно особым образом расположить в ряд элементы группы G. Для этого используем тот факт, что группу G можно представить в виде объединения всевозможных непересекающихся правых классов смежности по подгруппе G_a, имеющих одинаковое число элементов. То есть существуют перестановки γ₀=ε, γ₁, …, γ _{l -1} из группы G такие, что все перестановки ряда

α ₀₌ β₀° γ₀= ε, α ₁ = β₁° γ₀, …, α _{s -1} = β _{s -1} ° γ₀,

α_{s =} β₀° γ₁, α_{s +1} = β₁° γ₁, …, α_{2 s -1} = β _{s -1} ° γ₁,                                        (*)

- - - - - - - - - - - - - - - - - - - - - - - - - - - -

α_(l-1)s= β ₀ ° γ _l-1, α_(l-1)s+1= β ₁ ° γ _l-1, …, α _ls-1 = β _s-1 ° γ _l-1

попарно различны и исчерпывают всю группу G.

Для любого i =0, …, l -1 применение s перестановок α _is, α _{is +1}, …, α_{( i +1) s -1}, образующих i -тую строку таблицы (*), к элементу а даёт один и тот же элемент γ _i (а) (так как β₀, β₁, …, β _{s -1} оставляют а неподвижным). Все l элементов γ _i (а) попарно различны. Действительно, если бы γ _i (а)=γ _j (а) для некоторых i, j, то а=(γ _j ° γ _i ^-1) (a), то есть перестановка (γ _j ° γ _i ^-1) G_a. Но это возможно только тогда, когда γ _i и γ _j содержатся в одном правом классе смежности группы G по подгруппе G_a, чего быть не может. Таким образом, длина орбиты О(а) равна l, то есть числу строк в таблице (*): k = l ∙ s (то есть l является индексом подгруппы в группе). По теореме Лагранжа l =| G |:| G_a |, то есть | O (a)|= | G |:| G_a |. Теорема доказана.

Теперь ответим на первый вопрос. Для этого сформулируем и докажем лемму Бернсайда.

Пусть λ(α) – число неподвижных точек перестановки α, t (G) – число орбит группы перестановок G ={ ε = α ₀, α ₁, …, α_{k -1} }, действующей на множестве М={1, 2, …, n }. Тогда для любой группы перестановок имеет место равенство:

t (G)= λ(α),           где α G.

Доказательство. Рассмотрим отношение «перестановка α сохраняет неподвижным элемент m» между перестановками группы G и элементами множества М. Сопоставим парам (α, m), α G, m M, вершины прямоугольной сети и отметим те из них, для которых соответствующая пара (α, m) находится в указанном отношении, то есть α(m)= m (рис. 1).

Ин ыми словами, построим график указанного отношения.

 

Число отмеченных точек (точек, принадлежащих графику) можно подсчитать двумя способами: определить число отмеченных точек на каждой вертикали и просуммировать полученные величины или же определить число таких точек на каждой горизонтали и вычислить их сумму. Согласно определению отношения на каждой вертикали отмечаются все точки, сохраняемые перестановкой α, соответствующей этой вертикали. Их число равно λ(α). Поэтому число всех точек графика равно

λ (α ₀) + λ (α ₁) + … + λ (α _k-1)= λ (α), где α G.

С другой стороны, на каждой горизонтали отмечаются все перестановки, сохраняющие элемент m M, отвечающий этой горизонтали. А такие перестановки образуют группу G_m – стабилизатор элемента m, - и их число, по теореме, доказанной ранее, равно | G_m |=| G |:| O (m)|. Поэтому при втором способе подсчёта числа отмеченных точек графика рассматриваемого отношения получаем выражение | G ₁ | + | G ₂ | + … + | G_n | = | G_m |(m M).

Однако, если элементы i, j M содержатся в одной орбите, то О(i)= O (j), и поэтому | G_i |=| G |:| O (i)|=| G |:| O (j)|=| G_j |. Пусть О₁, О₂, …, О _t – все орбиты группы G такие, что , и слагаемые в этом объединении не пересекаются. Разобьём | G_m | (где m M) на части так, чтобы внутри каждой из этих частей суммирование шло по элементам некоторой орбиты:

_m | 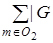= _m | + _m | + … + _m |.

Каждое из t слагаемых в правой части этого равенства можно преобразовать следующим образом:

_m| =  =  =  = | G |.

Поэтому _m| = | G | + … +| G | = t ∙| G |.

Таким образом, при втором способе подсчёта мы получили t ∙| G | отмеченных точек графика. Приравнивая величины, полученные при первом и втором способах, получим

t | G | = ,

то есть t = t (G) = .

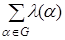Лемма доказана.

 

Комбинаторные задачи

Рассмотрим несколько примеров, иллюстрирующих возможности применения леммы Бернсайда при решении комбинаторных задач на перечисление.

Задача 1. Сколькими способами можно раскрасить вершины куба в три цвета (например, красный, синий и зелёный)?

Решение. (В остальных задачах будем использовать обозначения, аналогичные обозначениям в этой задаче). Поскольку каждую из восьми вершин куба можно раскрасить тремя способами, причём независимо от того, как раскрашены другие вершины, то множество всех вершин куба можно раскрасить 3⁸=6561 различными способами (по формуле 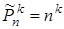). Однако при таком подходе к решению задачи молчаливо предполагается, что мы умеем различать вершины куба перед окраской, то есть, скажем, куб жёстко закреплён или его вершины занумерованы. При этом полученный ответ можно интерпретировать следующим образом: можно так раскрасить 3⁸ абсолютно одинаковых, жёстко закреплённых кубов, что все они будут различаться. Для 3⁸+1 кубов этого сделать уже нельзя. Ситуация существенно меняется, если мы откажемся от предположения о том, что кубы жёстко закреплены, так как по-разному окрашенные кубы можно повернуть так, что в новом положении их окраски совпадут (рис.2).

Естественно считать, что два куба раскрашены одинаково, если их раскраски совпадают вплоть до способа размещения кубов в пространстве, то есть вплоть до некоторого вращения одного из кубов. Будем говорить, что такие раскраски кубов геометрически неотличимы. Поэтому естественным уточнением задачи о раскраске является следующая задача: сколькими геометрически различными способами можно раскрасить вершины куба в три цвета.

Переформулируем теперь эту задачу так, чтобы стала понятной её связь с леммой Бернсайда. Пусть М – множество всевозможных по-разному раскрашенных кубов одного размера, положение которых в пространстве фиксировано (| M |=3⁸), G – группа всех вращений куба. Группа G естественным образом определяет группу перестановок на множестве М. Именно, если α G – некоторое вращение, то каждому кубу из М можно сопоставить некоторый другой куб, который получается из первого при вращении α. Это соответствие является перестановкой на М, которую будем обозначать . Группу всех таких перестановок множества М, определяемых перестановками из G будем обозначать . Ясно, что | | = | G |. То, что два куба К₁ и К ₂ из М раскрашены геометрически одинаково, означает, что один из них можно перевести вращением в такое положение, в котором они неразличимы. Иными словами, существует такая перестановка , что (К₁) = К₂, то есть К₁ и К₂ содержатся в одной орбите группы , действующей на множестве М. Таким образом, для того чтобы определить число геометрически различимых способов раскраски вершин куба, нужно найти количество орбит группы  на множестве М. Считая вершины кубов занумерованными числами 1, 2, 3, 4, 5, 6, 7, 8, раскраску каждого из 3⁸ кубов можно однозначно охарактеризовать «словом» из восьми букв, каждая из которых есть либо к, либо с, либо з. То, что i -тая буква слова равна к (или с, или з) означает, что i -тая вершина при выбранной нумерации окрашена в красный цвет (или в синий, или в зелёный соответственно). Перестановки из группы  переставляют последовательности букв к, с, з. Для того чтобы применить лемму Бернсайда, необходимо определить число неподвижных точек каждой перестановки из . 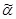Последовательность букв к, с, з будет неподвижной для перестановки  тогда и только тогда, когда при разложении соответствующей перестановки α G в произведение циклов вершины куба, номера которых входят в один и тот же цикл, окрашены одним цветом. Если перестановка α G разложена в произведение k циклов, то число её неподвижных точек равно 3 ^k, где , так как вершины куба, номера которых входят в один цикл, можно раскрасить тремя способами. Опишем разложения в произведение циклов для всех перестановок из группы G вращений куба.

а) Вокруг каждой из трёх осей, соединяющих центры противоположных граней, имеется три вращения на углы , , . Им соответствуют перестановки:

1) (1, 5, 8, 4) (2, 6, 7, 3)

2) (1, 8) (2, 7) (3, 6) (4, 5)

3) (1, 4, 8, 5) (2, 3, 7, 6)

4) (1, 4, 3, 2) (5, 8, 7, 6)

5) (1, 3) (2, 4) (5, 7) (6, 8)

6) (1, 2, 3, 4) (5, 6, 7, 8)

7) (1, 5, 6, 2) (3, 4, 8, 7)

8) (1, 6) (2, 5) (3, 8) (4, 7)

9) (1, 2, 6, 5) (3, 7, 8, 4)

б) Вокруг каждой из четырёх диагоналей куба имеется по два вращения. Им соответствуют перестановки:

10) (1) (2, 5, 4) (3, 6, 8) (7)

11) (2) (1, 3, 6) (4, 7, 5) (8)

12) (3) (1, 6, 8) (2, 7, 4) (5)

13) (4) (1, 3, 8) (2, 7, 5) (6)

14) (1) (2, 4, 5) (3, 8, 6) (7)

15) (2) (1, 6, 3) (4, 5, 7) (8)

16) (3) (1, 8, 6) (2, 4, 7) (5)

17) (4) (1, 8, 3) (2, 5, 7) (6)

в) Вокруг каждой из шести осей, соединяющих середины противоположных рёбер куба, имеется одно вращение. Им соответствуют перестановки:

18) (1, 5) (2, 8) (3, 7) (4, 6)

19) (1, 2) (3, 5) (4, 6) (7, 8)

20) (1, 7) (2, 3) (4, 6) (5, 8)

21) (1, 7) (2, 6) (3, 5) (4, 8)

22) (1, 7) (2, 8) (3, 4) (5, 6)

23) (1, 4) (2, 8) (3, 5) (6, 7)

Вместе с тождественной перестановкой (1)(2)(3)(4)(5)(6)(7)(8) получаем 24 перестановки – все элементы группы G. Итак, в группе G вращений куба имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1, 1, 1>,

6 перестановок типа <4, 4>,

9 перестановок типа <2, 2, 2, 2>,

8 перестановок типа <1, 1, 3, 3>.

Тогда перестановка первого типа имеет 3⁸ неподвижных точек, любая из перестановок второго типа – 3², третьего и четвёртого типов – 3⁴ неподвижных точек (по формуле _n^k = n^k). Поэтому согласно лемме Бернсайда, имеем (3⁸ + 6∙3² + 9∙3⁴ + 8∙3⁴) = 333.

Таким образом, число геометрически различимых способов раскраски вершин куба в три цвета равно 333.

Задача 2. Сколько различных ожерелий из семи бусин можно составить из бусин двух цветов – красного и синего?

Решение. Переформулируем эту задачу следующим равносильным образом: сколькими геометрически различными способами можно раскрасить вершины правильного семиугольника в два цвета? Пусть М – множество всевозможных по-разному раскрашенных правильных семиугольников одного размера, положение которых в пространстве фиксировано. Тогда имеется 2⁷ = 128 различных вариантов раскраски вершин семиугольника, так как каждую вершину независимо от других можно раскрасить двумя способами. Здесь два способа раскраски неотличимы, если один из них можно получить из другого, применяя к семиугольнику либо преобразования вращения, либо симметрии относительно осей. Будем описывать раскраски «словами» длины 7, составленными из букв к (вершина окрашена в красный цвет) и с (вершина окрашена в синий цвет). Проделаем те же действия, что и в задаче 1 для применения леммы Бернсайда. Опишем разложения в произведение циклов для всех перестановок из группы G.

а) Тождественному преобразованию соответствует перестановка:

1) (1)(2)(3)(4)(5)(6)(7)

б) Поворотам на углы  соответствуют перестановки:

2) (1,2,3,4,5,6,7)

3) (1,3,5,7,2,4,6)

4) (1,4,7,3,6,2,5)

5) (1,5,2,6,3,7,4)

6) (1,6,4,2,7,5,3)

7) (1,7,6,5,4,3,2)

в) Симметриям относительно осей, соединяющих вершины семиугольника с серединами противоположных сторон, соответствуют перестановки:

8) (1) (2,7) (3,6) (4,5)

9) (2) (1,3) (7,4) (5,6)

10) (3) (2,4) (1,5) (6,7)

11) (4) (3,5) (2,6) (7,1)

12) (5) (4,6) (3,7) (2,1)

13) (6) (5,7) (4,1) (2,3)

14) (7) (1,6) (2,5) (3,4),

где 1, 2, 3, 4, 5, 6, 7 – числа, с помощью которых занумерованы вершины семиугольника.

Итак, в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1, 1>,

6 перестановок типа <7>,

7 перестановок типа <1, 2, 2, 2>.

Слово неподвижно относительно перестановки  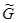тогда и только тогда, когда буквы, стоящие на местах с номерами из одного цикла в перестановке α, совпадают. Поэтому тождественная перестановка имеет 2⁷ неподвижных точек на М, перестановки второго типа – по 2, а перестановки третьего типа – по 2⁴. Применяя лемму Бернсайда, получаем

(2⁷ + 6∙2 + 7∙2⁴) = 18.

Итак, из бусин двух цветов можно составить 18 семибусенных ожерелий.

Задача 3. Грани куба можно раскрасить: а) все в белый цвет; б) все в чёрный цвет; в) часть в белый, а остальные в чёрный. Сколько имеется разных способов раскраски?

Решение.

Грань (1' 4' 5' 8') – 1

Грань (2' 3' 6' 7') – 2

Грань (3' 4' 7' 8') – 3

Грань (1' 2' 5' 6') – 4

Грань (1' 2' 3' 4') – 5

Грань (5' 6' 7' 8') – 6

 

Рис. 3

а) Вокруг каждой из трёх осей, соединяющих центры противоположных граней, имеется три вращения на углы , , . Им соответствуют перестановки:

1) (1) (2) (5, 4, 6, 3)

2) (1) (2) (4, 3) (6, 5)

3) (1) (2) (5, 3, 6, 4)

4) (3) (4) (1, 6, 2, 5)

5) (3) (4) (1, 2) (6, 5)

6) (3) (4) (5, 2, 6, 1)

7) (5) (6) (1, 3, 2, 4)

8) (5) (6) (1, 2) (3, 4)

9) (5) (6) (4, 2, 3, 1)

б) Вокруг каждой из четырёх диагоналей куба имеется по два вращения. Им соответствуют перестановки:

10) (2, 6, 3) (1, 5, 4)

11) (3, 6, 2) (4, 5, 1)

12) (6, 4, 2) (1, 5, 3)

13) (2, 4, 6) (3, 5, 1)

14) (1, 3, 6) (2, 4, 5)

15) (6, 3, 1) (5, 4, 2)

16) (1, 4, 6) (2, 3, 5)

17) (6, 4, 1) (5, 3, 2)

в) Вокруг каждой из шести осей, соединяющих середины противоположных рёбер куба, имеется одно вращение. Им соответствуют перестановки:

18) (2, 3) (1, 4) (5, 6)

19) (1, 3) (4, 2) (5, 6)

20) (1, 6) (5, 2) (3, 4)

21) (1, 5) (6, 2) (3, 4)

22) (4, 6) (3, 5) (1, 2)

23) (6, 3) (5, 4) (1, 2)

Вместе с тождественной перестановкой (1)(2)(3)(4)(5)(6) получаем 24 перестановки – все элементы группы G. Итак, в группе G вращений куба имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1>,

6 перестановок типа <1, 1, 4>,

3 перестановки типа <1, 1, 2, 2>,

8 перестановок типа <3, 3>,

6 перестановок типа <2, 2, 2>.

Поэтому тождественная перестановка имеет 2⁶ неподвижных точек на М, перестановки второго и пятого типов имеют по 2³ неподвижных точек на М, перестановки третьего типа – по 2⁴, а перестановки четвёртого типа – по 2². Тогда по лемме Бернсайда получаем (2⁶ + 6∙2³+ 3∙2⁴+ 8∙2² + 6∙2³) = 10.

Итак, число геометрически различных способов раскраски граней куба в два цвета равно 10.

Задача 4. Сколько различных ожерелий можно составить из двух синих, двух белых и двух красных бусин?

Решение. Переформулируем задачу так: сколькими геометрически различными способами можно раскрасить вершины правильного шестиугольника так, чтобы две были синего цвета, две – белого, две – красного? а) Вокруг центра шестиугольника имеется пять поворотов на углы . Им соответствуют перестановки:

1) (1, 2, 3, 4, 5, 6)

2) (1, 3, 5) (2, 4, 6)

3) (1, 4) (2, 5) (3, 6)

4) (1, 5, 3) (2, 6, 4)

5) (1, 6, 5, 4, 3, 2)

б) Имеется три симметрии относительно осей, соединяющих противоположные вершины правильного шестиугольника. Им соответствуют перестановки:

6) (1) (4) (2, 6) (3, 5)

7) (2) (5) (3, 1) (4, 6)

8) (3) (6) (2, 4) (1, 5)

в) Имеется три симметрии относительно осей, соединяющих середины противоположных сторон правильного шестиугольника. Им соответствуют перестановки:

9) (1, 2) (6, 3) (5, 4)

10) (1, 6) (2, 5) (3, 4)

11) (2, 3) (1, 4) (6, 5)

Вместе с тождественной перестановкой (1) (2) (3) (4) (5) (6) получаем 12 перестановок – все элементы группы G. Итак, в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1>,

2 перестановки типа <6>,

2 перестановки типа <3, 3>,

4 перестановки типа <2, 2, 2>,

3 перестановки типа <1, 1, 2, 2>.

Определим количество неподвижных точек для перестановок каждого типа. Так как количество различных цветов, в которые нужно раскрасить шестиугольник, равно трём, то минимальное количество циклов в перестановке должно быть равно трём, чтобы она имела неподвижные точки. То есть перестановки 1), 2), 4), 5) неподвижных точек не имеют. Для перестановки первого типа получим ₃⁶ =  = 90 неподвижных точек. Для каждой перестановки типа <2, 2, 2> по принципу умножения получаем по Р ₃ = 3∙2∙1= 6 неподвижных точек. Для каждой перестановки типа <1, 1, 2, 2> по принципу умножения получим по Р ₃ = 3∙2∙1∙1= 6 неподвижных точек. Применим лемму Бернсайда: 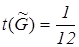(1∙90+ 4∙6+ 3∙6) = 11.

Итак, 11 различных ожерелий можно составить из двух синих, двух белых, двух красных бусин.

Задача 5. Сколькими геометрически различными способами три абсолютно одинаковые мухи могут усесться в вершинах правильного пятиугольника?

Решение. Обозначим М – множество различных способов расположения трёх одинаковых мух в вершинах пятиугольника, если вершины занумерованы. Тогда | M | = ₂⁵ (3, 2)= =10 способов расположения мух, где 2 – количество элементов множества М₁ = {м, с} (где м – муха, с – свободная вершина),

3, 2 – кратности соответственно м и с.

а) Вокруг центра пятиугольника имеется четыре поворота на углы . Им соответствуют перестановки:

1) (1, 2, 3, 4, 5)

2) (1, 3, 5, 2, 4)

3) (1, 4, 2, 5, 3)

4) (1, 5, 4, 3, 2)

б) Имеется пять симметрий относительно осей, соединяющих вершины пятиугольника с серединами противоположных сторон. Им соответствуют перестановки:

5) (1) (2, 5) (3, 4)

6) (2) (1, 3) (5, 4)

7) (3) (2, 4) (1, 5)

8) (4) (3, 5) (2, 1)

9) (5) (1, 4) (2, 3),

где 1, 2, 3, 4, 5 – числа, с помощью которых занумерованы вершины пятиугольника. Вместе с тождественной перестановкой (1)(2)(3)(4)(5) имеем 10 элементов группы G. Итак, в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1>,

4 перестановки типа <5>,

5 перестановок типа <1, 2, 2>.

Определим количество неподвижных точек для перестановок каждого типа. Чтобы перестановка имела неподвижные точки, минимальное количество циклов в перестановке должно быть равно двум, так как множество М₁ состоит из двух элементов м и с. Поэтому перестановки 1) – 4) не имеют неподвижных точек. Тогда для перестановки типа <1, 1, 1, 1, 1> имеем по формуле: ₂⁵ (3, 2) = = 10 неподвижных точек. Для каждой перестановки типа <1, 2, 2> получим по принципу умножения по Р ₂ = 2∙1∙1= 2 неподвижные точки. По лемме Бернсайда получаем (1∙10+ 5∙2) = 2.

Итак, двумя геометрически различными способами три одинаковые мухи могут усесться в вершинах правильного пятиугольника.

Задача 6. Сколькими способами можно раскрасить вершины куба в два цвета (красный и синий) так, чтобы вершин каждого цвета было поровну?

Решение. Для решения этой задачи воспользуемся задачей 1. Пусть М – множество всевозможных по-разному раскрашенных кубов одного размера, положение которых в пространстве фиксировано. Тогда по формуле _n ^k (k ₁, k ₂, …, k_n) =   получим | M | = ₂⁸ (4,4) = 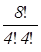= 70 по-разному раскрашенных кубов. Так как нам нужно раскрасить вершины в два цвета (4 - в красный, 4 - в синий), то минимальное количество циклов в перестановке должно быть равно двум. Поэтому все перестановки 1) – 24) (задача 1) имеют неподвижные точки. В результате в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1, 1, 1>,

6 перестановок типа <4, 4>,

9 перестановок типа <2, 2, 2, 2>,

8 перестановок типа <1, 1, 3, 3>.

Тогда перестановка типа <1, 1, 1, 1, 1, 1, 1, 1> имеет ₂⁸ (4,4) = = 70 неподвижных точек. Каждая перестановка типа <4, 4> имеет (по принципу умножения Р ₂ = 2∙1= 2 неподвижные точки. Для каждой перестановки типа <2, 2, 2, 2> имеется ₂⁴ (2, 2) = = 6 неподвижных точек. Каждая перестановка типа <1, 1, 3, 3> имеет (по принципу умножения) Р ₂ = 2∙1∙2∙1= 4 неподвижные точки. По лемме Бернсайда получаем 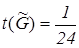(1∙70+ 6∙2 + 9∙6 + 8∙4) = 7.

Итак, семью способами можно раскрасить вершины куба в два цвета так, чтобы вершин каждого цвета было поровну.

Задача 7. Сколькими различными способами можно грани куба раскрасить в четыре цвета так, чтобы все четыре цвета присутствовали в раскраске каждого куба?

Решение. Для решения этой задачи воспользуемся задачей 3. Пусть М – множество всевозможных по-разному раскрашенных кубов одного размера, положение которых в пространстве фиксировано. Тогда по принципу умножения: первую грань можно раскрасить 4 способами, вторую – тремя, третью – двумя, четвёртую – одним способом, пятую – четырьмя, шестую – четырьмя способами. Получим | M | = 4∙3∙2∙1∙4∙4 = 384. Найдём геометрически различные способы раскраски. Для этого используем описанные в задаче 3 разложения в произведение циклов всех перестановок из группы G вращений куба. Так как в раскраске куба должны присутствовать четыре разных цвета, то минимальное количество циклов в перестановке должно быть равно четырём. Поэтому перестановки 1), 3), 4), 6), 7), 9) – 23) в задаче 3 неподвижных точек не имеют. Таким образом, неподвижные точки имеют 3 перестановки типа <1, 1, 2, 2> и 1 перестановку типа <1, 1, 1, 1, 1, 1>. Определим количество неподвижных точек для перестановок каждого типа. Для перестановки типа <1, 1, 1, 1, 1, 1> имеем по принципу умножения Р₄ = 4∙3∙2∙1∙4∙4 = 384 неподвижные точки. Для каждой перестановки типа <1, 1, 2, 2> по принципу умножения имеется Р₄ = 4∙3∙2∙1 = 24 неподвижные точки. По лемме Бернсайда получаем (1∙384+3∙24) = 19.

Итак, существует 19 различных способов раскраски граней куба в 4 цвета так, чтобы все 4 цвета присутствовали в раскраске каждого куба.

§ 2. «Метод просеивания» [4]

Познакомимся с наиболее общим методом пересчёта, который можно назвать «методом просеивания» или «комбинаторным просеиванием»: с любым свойством P можно связать его расщепление на некотором множестве A, в соответствии с которым A разбивается на две части: подмножество А₁, образованное элементами, обладающими свойством Р, и А₂, образованное элементами, не обладающими свойством Р, т. е. обладающими свойством . Выбирая свойства подходящим образом, можно последовательным просеиванием пересчитать подмножества с наложенными на них теми или иными ограничениями.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: