 |
Тригонометрические преобразования.
|
|
|
|
Кроме различных арифметических преобразований типа разложения многочленов или дробей, существуют задачи, в которых нужно выполнить тригонометрические преобразования подынтегральной функции.
Задача 10. Вычислить интеграл 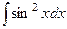 .
.
Решение. Воспользуемся формулой понижения степени, чтобы перейти от степеней тригонометрических функций к выражениям типа  или
или 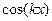 .
.
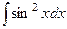 =
=  =
= 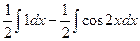 =
= 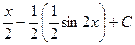 .
.
Ответ. 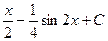 .
.
Задача 11. Вычислить 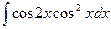 .
.
Решение. Здесь можно было бы применить формулу для косинуса двойного угла, но это преобразование бы только увеличило степени. Поэтому в данном случае для удобнее применить формулу понижения степени ко второму множителю и не менять первый.
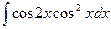 =
=  =
= 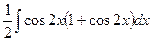 =
=
= 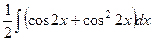 =
=  .
.
Первый интеграл вычисляется уже известным способом, а во втором снова понизим степень.
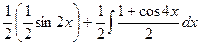 =
= 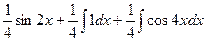 =
= 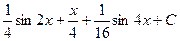 .
.
Ответ. 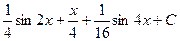 .
.
Подведение под знак дифференциала.
Задача 12. Вычислить 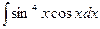 .
.
Решение. Замечаем, что присутствует множитель 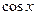 , который является производной от
, который является производной от 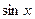 . А остальная часть функции как раз зависит только от
. А остальная часть функции как раз зависит только от 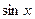 . Поэтому можно подвести
. Поэтому можно подвести 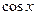 под знак дифференциала:
под знак дифференциала: 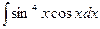 =
= 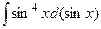
Применяем замену 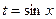 :
: 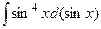 =
= 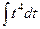 .
.
Далее, 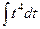 =
= 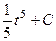 , и после обратной замены
, и после обратной замены  .
.
Ответ.  .
.
Задача 13. Вычислить интеграл  .
.
Решение.  =
= 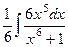 =
= 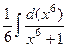 =
= 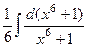 =
= 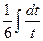 =
=
=  =
= 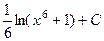 . Учитывая тот факт, что
. Учитывая тот факт, что 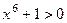 , знак модуля не нужен.
, знак модуля не нужен.
Ответ. 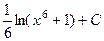 .
.
Задача 14. Вычислить 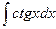 .
.
Решение. 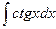 =
=  =
=  =
= 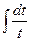 =
= 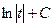 =
= 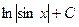 .
.
Ответ. 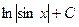 .
.
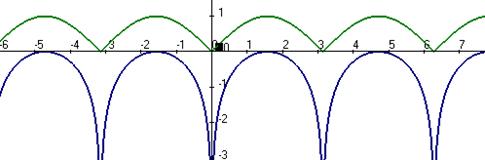
Для сведения, покажем, как выглядит график функции 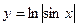 .
.
Зелёным цветом изображён график 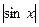 , синим
, синим  .
.
Вертикальные асимптоты 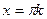 .
.
Задача 15. Вычислить интеграл 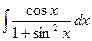 .
.
Решение. 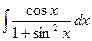 =
= 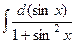 =
=  =
= 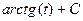 =
=
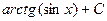 . Ответ.
. Ответ. 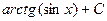 .
.
Домашнее задание.
1. Вычислить интеграл 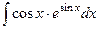 . Ответ.
. Ответ.  .
.
2. Вычислить интеграл 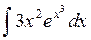 . Ответ.
. Ответ. 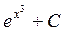 .
.
3. Вычислить интеграл 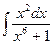 . Ответ.
. Ответ. 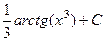 .
.
4. Вычислить интеграл 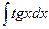 . Ответ.
. Ответ. 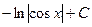 .
.
ПРАКТИКА № 2
Задача 1. Вычислить 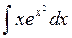 .
.
Решение. 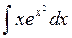 =
= 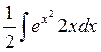 =
= 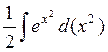 =
= 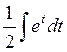 =
=  =
=  .
.
Ответ.  .
.
Задача 2. Вычислить 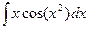 .
.
|
|
|
Решение. 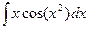 =
= 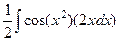 =
= 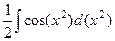 =
=
= 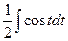 =
=  =
=  .
.
Ответ.  .
.
Задача 3. Вычислить 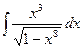 .
.
Решение. 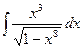 =
= 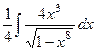 =
= 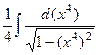 =
= 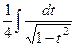 =
= 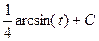 =
= 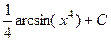 .
.
Ответ. 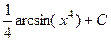 .
.
Задача 4. Вычислить 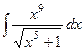 .
.
Решение. Если сразу подвести под знак дифференциала то, что есть в числителе, то будет 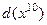 , но тогда в знаменателе получится выражение
, но тогда в знаменателе получится выражение 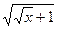 . чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через
. чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через 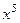 .
.
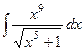 =
= 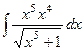 =
= 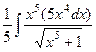 =
= 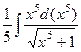
и теперь, после замены 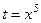 , получится
, получится 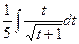 .
.
Далее, сделаем преобразование, котрое позволит оставить только однотипные корни:
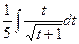 =
= 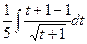 =
= 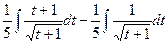 =
=
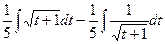 =
= 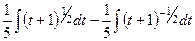
далее уже с помощью обычных действий со степенными функциями:
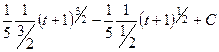 =
= 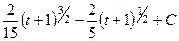 .
.
После обратной замены получаем ответ, при этом также заодно обратно меняем дробные степени на корни.
Ответ. 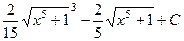 .
.
Задача 5. Вычислить  .
.
Решение.  =
= 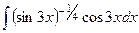 =
=
= 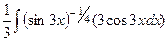 =
= 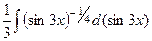 =
=  =
=
 =
= 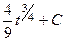 =
=  .
.
Ответ. 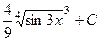 .
.
Задача 6. Вычислить  .
.
Решение. Заметим, что в числителе производная того выражения, которое есть в знаменателе. Тогда  =
=  =
= 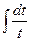 =
= 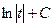 =
= 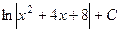 .
.
Здесь фактически мы применили замену  для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду
для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду 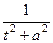 .
.
Ответ. 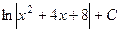 .
.
Задача 7. Вычислить 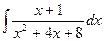 .
.
Решение. Здесь, в отличие от прошлой задачи, в числителе уже произвольный многочлен, не соответствующий производной от знаменателя. Тем не менее, можно путём арифметических операций получить там дифференциал знаменателя:
Домножим и поделим на 2, чтобы исправился коэффициент при 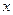 :
:
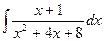 =
= 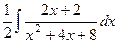
Теперь осталось прибавить и отнять 2, и будет получено 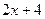 :
:
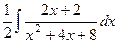 =
= 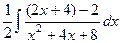 =
=
= 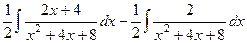 .
.
В первом слагаемом делается ровно то же самое, что в прошлой задаче, а во втором - выделить полный квадрат, и в итоге сводится к арктангенсу:
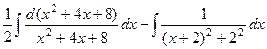 =
=
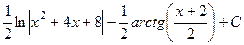 .
.
Ответ. 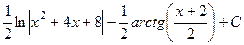 .
.
Задача 8. Вычислить 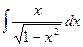 .
.
Решение. Несмотря на то, что интеграл похож на 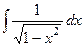 , но, тем не менее, в числителе есть переменная
, но, тем не менее, в числителе есть переменная 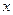 , поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.
, поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.
|
|
|
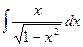 =
= 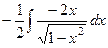 =
= 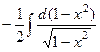
после замены переменной, это можно переписать так: 
а значит, 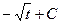 и после обратной замены:
и после обратной замены:
Ответ. 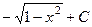 .
.
Задача 9. Вычислить 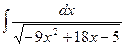 .
.
Решение. 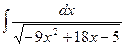 =
= 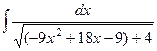 =
=  =
=  =
=  .
.
Для того, чтобы применить формулу, 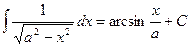
нужно обозначить 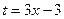 . Но сначала сделаем так, чтобы и в числителе оказался не просто
. Но сначала сделаем так, чтобы и в числителе оказался не просто  а
а  :
:
 =
= 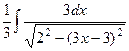 =
= 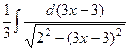 .
.
Теперь интеграл имеет вид 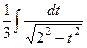 , и равен
, и равен 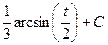 .
.
После обратной замены получаем ответ.
Ответ. 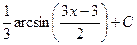 .
.
|
|
|


