 |
ПРАКТИКА № 7 (14 марта у обеих групп).
|
|
|
|
Сегодня в первые 45 минут мы решим несколько задач, оставаясь в рамках темы «определённый интеграл» но при этом интегралы будут содержать такие функции, действия над которыми нужно повторить для контрольной работы.
Задача 1. Вычислить интеграл 
.
При этом осуществляется повторение темы «элементарные преобразования, подведение под знак дифференциала».
Решение. = 
= 
=
= 
=
= 
.
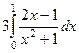Ответ. .
Задача 2. Вычислить интеграл 
.
При этом осуществляется повторение темы «рациональные дроби».
Решение. Сначала представим дробь в виде суммы простейших.
. При приведении к общему знаменателю, числитель получится такой:
, что равно 
, 
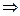
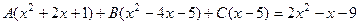
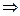
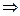
система: 
решим её методом Гаусса.
.
Здесь от 2-й строки отняли удвоенную 1-ю и от 3-й 1-ю, а затем от 3-й строки 2-ю. Основная матрица системы стала треугольной, и С находится сразу же: 
. Тогда 
и тогда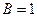 
. Из 1-го уравнения тогда уже получается 
.
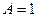Значит, исходный интеграл распадается на сумму 3 интегралов: 
= 
=
= 
= 
.
Ответ. .
Задача 3. Вычислить интеграл 
.
При этом осуществляется повторение темы «интегрирование иррациональностей».
Решение. НОК(2,4) = 4, поэтому замена 
. При такой замене 
, 
, 
. 
.
= 
= 
= 
= 
=
= 
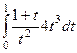. Ответ. .
Задача 4. Вычислить интеграл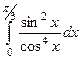 
.
При этом осуществляется повторение темы «интегрирование тригонометрических функций».
Решение. Суммарная степень чётна, поэтому применяется замена
, тогда 
, 
, 
.
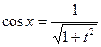Пересчитаем границы.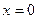 
, 
.
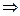
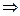
Итак, подставим всё это в интеграл.
= 
= 
=
= 
= 
= 
= 
= 
.
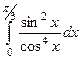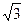Ответ. .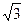
Контрольная работа: 45 минут
1. Подведение под знак дифференциала, преобразования.
2. Интегрирование по частям.
3. Интегрирование рациональных дробей.
4. Интегрирование иррациональностей и тригонометрических функций.
|
|
|
ПРАКТИКА № 8.
Задача 1. Найти площадь фигуры, ограниченной линиями:
и 
.
Решение. Рассмотрим чертёж, найдём точки пересечения графиков и увидим, какую часть плоскости они ограничивают.
График имеет максимум в точке 0 и проходит выше, чем , у которой, напротив, там минимум. Точки перечечения 
, 
. Все функции в интеграле чётные, фигура симметрична, можно вычислить площадь правой половины и удвоить: 
= 
= 
= 
= 
. Ответ. .
Задача 2. Найти площадь области, ограниченной линиями 
Решение.
= 
= 
= 
= 
.
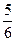Чертёж:
Ответ. .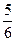
Задача 3. Найти площадь фигуры, ограниченной линиями: 
.
Решение. Чертёж:
= 
= 
+ 
для раскрытия 1-го слагаемого, вспомним пример из лекйиц на интегрирование по частям, там делали именно этим методом.
Если 
, 
, 
, 
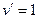то:
+ = 
+ =
+ = 
=
= 
.
Ответ. .
Задача 4. Найти объём, получающийся при вращении кривой 
, при условии что 
.
Решение. 
= 
= 
= 
= 
.
Ответ. .
Замечание. Эта задача может быть интерпретирована физическим примером: сколько воды может поместиться в эллиптический параболоид. Ведь если график корня повернуть на 90 градусов, это парабола.
Задача 5. С помощью основной формулы объёмов тел вращения, доказать формулу объёма конуса 
.
Решение. Для удобства применения основной формулы, повернём конус на 90 градусов, так, чтобы высота лежала на оси 
.
На чертеже видно, что два катета имеют длины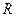 
и 
. Тогда отрезок, вращением которого образована боковая поверхность конуса, находится на прямой 
.
= 
= 
= 
= 
= 
= 
.
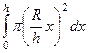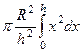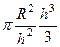Ответ: формула доказана.
Задача 6. Найти длину явно заданной кривой: 
.
Решение. Формула 
.
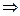
. Тогда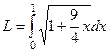 
=
= 
= 
=
= 
= 
.
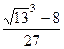Ответ. .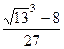
Задача 7. Найти длину 1 витка винтовой линии в пространстве 
Решение. В данном случае кривая параметрически задана, в 3-мерном пространстве. Формула 
.
Производные: 
.
= 
= 
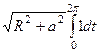
Ответ. 
.
Замечание. Если была бы не винтовая линия, а окружность, а это было бы при параметре 
, то как раз бы и получалось 
длина окружности.
|
|
|
Задача 8. Найти длину дуги х = cos3(2t), y =sin3(2t), 
Решение. Производные: 
Для удобства вычислений, сразу вынесем за скобки произведение:
.
Тогда: 
, 
= 
= 
= 
= 
= 
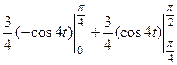= 3.
Ответ. 3.
Замечание. Если бы не учли знак модуля и не разбили на 2 части, тогда получилось бы неверно, ведь эти части бы не складывались, а взаимно уничтожались: 
Задача 9. Найти длину кривой, заданной в полярных координатах: 
, 
.
Решение. Формула: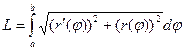 
.
, 
.
= 
= 
= 
= 
.
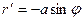дальше будем делать замену 
, но чтобы она задавалась монотонной функцией и не возникло противоречие в том, что пределы интегрирования 
и 0 в ответе, заранее разбиваем на 2 части и удваиваем интеграл.
, 
, 
, 
.
= 
= 
=
= 
= 
= 
=
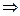
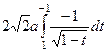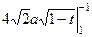. Ответ. 
.
Домашнее задание.
Найти длину кривой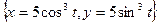 
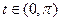. Ответ.15.
ПРАКТИКА № 9.
Несобственный интеграл.
Задача 1. Вычислить несобственный интеграл 1 рода 
.
Решение. = 
= 
= 
= 
= 
= 
.
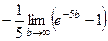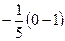Для краткости в будущем можно не использовать знак lim а просто записывать так: 
подразумевая при этом, что промежуточным действием был вычислен данный предел.
Ответ. .
Задача 2. Вычислить несобственный интеграл 1 рода 
.
Решение. На этом примере мы ещё раз вспомним метод интегрирования по частям.
= 
. Интегрируем по частям.
Обозначим 
. Тогда 
.
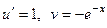Тогда далее 
= 
= 
=
= 1.
Ответ. 1.
Задача 3. Вычислить несобственный интеграл 1 рода 
.
Решение. = 
= 
=
= 
. Здесь символом 
фактически обозначается такой предел: 
.
Ответ. .
Задача 4. Вычислить несобственный интеграл 1 рода 
.
Решение. Кстати, на этом примере мы ещё раз повторим алгоритм выделения полного квадрата. = 
= 
= 
= 
= 
.
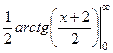Ответ. .
Задача 5. Вычислить несобственный интеграл 1 рода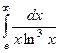 
.
Решение. =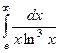 
= 
сделаем замену 
, далее 
= 
= 
= 
= 
= 
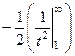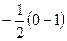. Ответ. .
Задача 6. Выяснить сходимость несобственного интеграла по признакам сравнения: 
, не вычисляя его.
Решение. В числителе степень 3, в знаменателе 4. Тогда в качестве эталонной функции, с которой надо сравнить, нужно взять такую: 
. Докажем, что с ней можно сравнивать функцию в этом интеграле, то есть вычислим предел их отношения и получим, что он равен числу, а не 0 или 
. 
= 
= 1.
Это эквивалентные величины, и сходимость исходного интеграла эквивалентна сходимости интеграла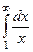 
. А этот интеграл расходится, так как степень равна 1 (см. теорию). Либо это видно из того, что первообразная в данном случае лограрифм, и она не ограниченная функция.
|
|
|
Ответ. Расходится.
Задача 7. Выяснить сходимость несобственного интеграла по признакам сравнения: 
, не вычисляя его.
Решение. Так как 
, то заменив функцию 
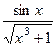на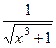 
, получим 
причём, по признаку сравнения в не-предельной форме, если второй интеграл сходится (обозначим его (II)), то и исходный тоже сходится. А теперь заменим на ещё более простую функцию, но уже по признаку сравнения в предельной форме.
Бесконечно малая величина 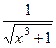при 
эквивалентна 
.
Докажем это: 
= 
= 
=1.
Поэтому сходимость интеграла эквивалентна сходимости интеграла 
. Обозначим его (III). А про этот интеграл уже известно, что он сходится, ведь здесь классический случай, рассмотренный в лекциях, а именно 
где степень 
. Итак, (III) сходится, что эквивалентно тому, что (II) сходится, а
(II) > (I), поэтому исходный интеграл (I) тоже сходится.
Ответ. Сходится.
Задача 8. Выяснить сходимость несобственного интеграла по признакам сравнения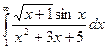 
не вычисляя его.
Решение. Аналогично прошлой задаче, сначала заменим на выражение без синуса с помощью неравенства, а потом перейдём к ещё более простому интегралу по предельному признаку.
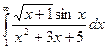
, а этот интеграл равен
, , сходится. Сходимость 2-го и 3-го эквивалентна, поэтому 2-й интеграл тоже сходится. А из сходимости 2-го следует сходимость 1-го.
Ответ. Сходится.
Задача 9. Выяснить сходимость несобственного интеграла 2-го рода по признакам сравнения 
.
Решение. = 
.
Особенность в 0 только у первого корня, второй там не даёт 0 в знаменателе. Заменим на эквивалентную, в качестве которой возьмём функцию только с тем множителем, который стремится к 0 в знаменателе при 
. 
. Докажем, что они эквивалентны:
= 
.
Значит, сходится 
сходится.
= 
, 
, что для интеграла 2 рода влечёт сходимость.
Либо можно рассмотреть = 
= 
.
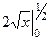
Ответ. Сходится.
Задача 10. Выяснить сходимость несобственного интеграла 2-го рода по признакам сравнения 
.
Решение. Заметим, что в знаменателе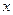 
и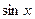 
, который в свою очередь эквивалентен 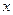(по 1 замечательному пределу). Поэтому можно взять 
. Обоснуем это с помощью предела:
|
|
|
= 
= 1.
Тогда остаётся выяснить сходимость интеграла 
. Он расходится, степень 2 > 1 что для интеграла 2-го рода влечёт расходимость.
Поэтому и исходный интеграл тоже расходится.
Ответ. Расходится.
Задача 11. Выяснить сходимость несобственного интеграла по признакам сравнения 
.
Решение. Это комбинированный пример на интеграл 1 и 2 рода.
Надо разбить на 2 части и исследовать отдельно окрестность 0 и оставшуюся часть полуоси.
= 
+ 
. Если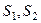 
оба числа конечны, то их сумма 
тоже конечна. То есть, для сходимости надо, чтобы оба этих интеграла сходились, один интеграл 1-го рода а другой 2-го рода.
Исследуем . Здесь эквивалентная величина подбирается по самым старшим степеням, ведь надо будет найти предел в .
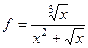, тогда 
.
= 
= 
.
Интеграл сходится 
сходится. А здесь 
, то есть он сходится.
Исследуем . Здесь эквивалентная величина подбирается по самым младшим степеням, ведь надо будет найти предел в 0.
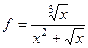, тогда 
.
= 
=. 
.
Интеграл 
сходится 
сходится. 
, что для интеграла 2 рода означает сходимость.
Итак, оба интеграла по 
и 
конечны, значит весь интеграл по 
тоже является конечным числом.
Ответ. Сходится.
Задача 12. Вычислить несобственный интеграл 2 рода 
.
Решение. Особенность в точке 1, впрочем, первообразная там может быть конечной, и мы даже не заметим, что интеграл несобственный:
= 
= 
= 
=
= 
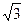= . Ответ. .
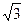Задача 13. Вычислить несобственный интеграл 2 рода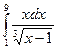 
.
Решение. Сделаем замену 
, тогда:
, 
, 
.
= 
= 
= 
=
= 
= 
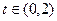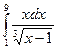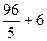= 19,2 + 6 = 25,2.
Ответ. 25,2.
Домашние задачи.
Выяснить сходимость: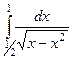 
(аналогично задаче 9).
Выяснить сходимость: 
(с разбивкой на 2 интервала в окрестности 0 и 2, как в задаче 11).
ПРАКТИКА № 10.
|
|
|
