 |
Классификация и общая характеристика задач нечеткого математического программирования
|
|
|
|
Лекция. Задачи нечеткого математического программирования
Вопросы:
Классификация и общая характеристика задач нечеткого математического программирования
Задача линейного программирования с нежестко заданными ограничениями
Задача линейного программирования с нечеткой целевой функцией
Задачи и упражнения
Многие современные задачи принятия решений в планировании и управлении производством характеризуются наличием недостоверных или неопределенных факторов. Такие ситуации отражают объективную недостаточную информированность лица, принимающего решение (ЛПР), о возможных количественных значениях этих факторов, а сам процесс принятия решений базируется на некоторых субъективных суждениях ЛПР. Подобные задачи называются задачами принятия решений при нечеткой информации, и модели принятия решения в этих условиях базируются на аппарате нечетких множеств Заде.
Рассмотрим классификацию моделей принятия решений при нечеткой информации.
1. По характеру описания предпочтений можно выделить:
- модели нечеткого математического программирования (НМП);
- модели нечетких отношений предпочтения на множестве допустимых альтернатив;
- модели нечеткой ожидаемой полезности;
- лингвистические модели принятия решений, основанные на нечеткой логике с лингвистическими значениями истинности.
2. По числу используемых критериев – однокритериальные и многокритериальные модели.
3. По числу ЛПР выделяют модели индивидуальных и коллективных решений.
4. По числу этапов модели принятия решений делятся на одноэтапные и многоэтапные.
Если модель принятия решений задана в виде целевой функции и ограничений, а нечеткость проявляется в форме нечеткости параметров этих функций или в виде исходного нечеткого множества допустимых альтернатив, то получают задачу нечеткого математического программирования (НМП).
|
|
|
Классификация и общая характеристика задач нечеткого математического программирования
Задача математического программирования в общем виде формулируется так:
при ограничениях 
,
где 
– целевая функция, 
– ограничение.
При моделировании реальных задач в такой форме нечеткость может проявиться в форме нечеткого описания функций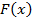 
, 
и параметров, от которых они зависят, и самого множества X. Подобное описание ситуации может отражать, например, недостаточность информации об этой ситуации или служить формой приближенного описания ситуации, достаточной для решения поставленной задачи.
Формы нечеткого описания бывают различными. Соответственно существуют разные классы задач НМП. Приведем некоторые типичные классы задач НМП.
Задача 1. Максимизация заданной обычной функции 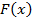на заданном нечетком множестве допустимых альтернатив Х.
Для решения этой задачи предлагается провести нормировку функции 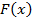следующим образом:
,
причем 
рассматривается как функция принадлежности нечеткого множества цели ЛПР. Значение этой функции интерпретируется как степень достижения цели при выборе альтернативы 
. Это позволяет применить к решению указанной задачи подход Беллмана – Заде, состоящий в следующем. Требуется найти такую альтернативу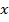 
, для которой достигается
Можно проверить, что задачу отыскания этой альтернативы можно сформулировать следующим образом:
найти 
при ограничениях: 
Задача 2. Нечеткий вариант стандартной задачи математического программирования. Пусть задана следующая задача НМП:
найти при ограничениях , 
Нечеткий вариант этой задачи получается если:
1) смягчить ограничения, то есть допустить возможность их нарушения с той или иной степенью;
|
|
|
2) вместо максимизации функции 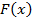можно стремиться достичь некоторого заданного значения 
этой функции, причем различным отклонениям 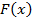от 
следует приписывать различные степени допустимости. Эту задачу можно записать так:
, 
где знак 
означает нечеткое выполнение соответствующих неравенств.
Один из возможных подходов к формализации подобных нечетко сформулированных задач состоит в следующем. Пусть - заданная величина целевой функции 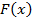, достижение которой считается достаточным для выполнения цели принятия решений, и пусть ЛПР задает два порога 
и 
такие, что неравенства 
означают сильное нарушение соответствующих неравенств 
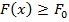. Тогда можно ввести следующие нечеткие множества цели и ограничений:
где 
– некоторые функции 
, описывающие степень выполнения соответствующих неравенств с точки зрения ЛПР. В результате исходная задача оказывается сформулированной в форме задачи достижения нечеткой цели и к ней можно применить подход Беллмана – Заде.
Задача 3. Нечетко описанная целевая функция, то есть задано отображение 
, где X - универсальное множество альтернатив, 
- числовая ось.
Здесь функция 
при каждом фиксированном 
— это нечеткое описание оценки результата выбора альтернативы, то есть нечеткая оценка альтернативы . Кроме того, задано нечеткое множество допустимых альтернатив с функцией принадлежности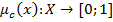 
. К такой постановке сводится весьма широкий класс задач НМП. Это наиболее известная постановка задачи НМП.
Задача 4. Задана обычная целевая функция 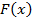и система ограничений 
, причем параметры в описаниях функций 
заданы в форме нечетких множеств. Например, для линейной функции имеют вид
,
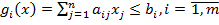где параметры 
являются элементами нечетких множеств с функциями принадлежности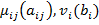 
. Указанный класс задач можно свести к задачам типа 1 или 3.
Задача 5. Функции 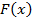, заданы с точностью до нечетко определенных параметров 
, которые являются элементами нечетких множеств с заданными функциями принадлежности 
. Этот класс задач можно свести к задачам типа 3.
|
|
|
