 |
Задача линейного программирования с нежестко заданными ограничениями
|
|
|
|
Задача вида
относится к задачам нечеткого линейного программирования и отличается от стандартной ЗЛП тем, что ограничения заданы нежестко, и могут «немного» нарушаться. Это происходит когда точные значения величин, стоящих в правой части ограничений, неизвестны, и вместо них используются нижние гарантированные оценки.
Один из способов сведения данной задачи к стандартному аналогу заключается в следующем. Вместо нахождения максимума целевой функции, зададим желаемое значение 
: 
.
Разным значениям целевой функции приписывается степень, с которой поставленная цель достигается. Если 
, то цель достигается со степенью, равной 1. В противном случае степень достижения желаемого результата строго меньше 1. Зададим параметры 
, определяющие «сильное» нарушение соответствующих ограничений. Будем считать, что ограничения нарушаются сильно, если
где символ 
используется для обозначения i-ой строки матрицы коэффициентов ограничений.
Некоторые авторы [4] предлагают выбирать значение , равное оптимальному значению целевой функции следующей задачи.
.
Тогда на допустимом множестве целевая функция примет значение, заведомо не превышающее .
Функции принадлежности 
для ограничений убывают на интервалах 
и принимают значения от 1 до 0. Полагая линейную зависимость функции внутри интервала, получим
Степень достижения целевого значения целевой функции определяется аналогично:
Для нахождения четкой альтернативы необходимо определить точку 
, имеющую максимальную степень принадлежности нечеткому решению, то есть
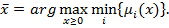
Согласно [4] такая альтернатива является решением задачи
,
.
Например. Рассмотрим решение ЗНМП, используя изложенный подход:
|
|
|
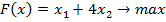
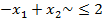
1. Зададим вектор допустимых нарушений ограничений и целевой функции 
.
2. Определим значение 
как оптимальное решение четкой задачи. Решение представлено на Рис. 3.1: 
=31,5.
3. Определим значение 
как оптимальное решение четкой задачи при максимальных нарушениях. Решение представлено на Рис. 3.2:
=38,5.
4. Определим значение 
.
5. Определим четкую альтернативу с максимальной степенью принадлежности нечеткому решению, решив следующую задачу.
Рис. 3.1 Решение четкой задачи
Рис.3.2 Решение задачи при максимальных нарушениях
Или после преобразования 
Каноническая форма задачи имеет вид:
– вспомогательные (уравновешивающие) переменные, 
- искусственные переменные и две целевые функции
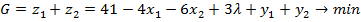
Решение задачи модифицированным симплеск-методом с использованием метода искусственного базиса представлено в Таблице 3.1.
Оптимальное решение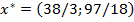 
допустимо со степенью 
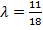и доставляет целевой функции значение 
. Это значение больше полученного при четких ограничениях.
Таблица 3.1
Симплекс-таблица решения задачи
| № | б.п. | x1 | x2 | 
| y1 | y2 | z1 | z2 | y3 | y4 | y5 | b | |
| z1 | -2 | -1 | |||||||||||
| z2 | -1 | -1 | |||||||||||
| y3 | -3 | ||||||||||||
| y4* | -1 | ||||||||||||
| y5 | |||||||||||||
| F | -1 | ||||||||||||
| G | -4 | -6* | |||||||||||
| z1 | -4 | ||||||||||||
| z2* | -2 | ||||||||||||
| y3 | -1 | ||||||||||||
| x2 | -1 | ||||||||||||
| y5 | -1 | ||||||||||||
| F | |||||||||||||
| G | -10* | ||||||||||||
| z1 | -1 | -2 | |||||||||||
| x1 | -1/5 | 1/5 | -2/5 | 2/5 | |||||||||
| y3 | -1/5 | 1/5 | 13/5 | 102/5 | |||||||||
| x2 | -1/5 | 1/5 | 3/5 | 17/5 | |||||||||
| y5* | 1/5 | -1/5 | -3/5 | 13/5 | |||||||||
| F | |||||||||||||
| G | -1 * | ||||||||||||
| z1* | -5 | ||||||||||||
| x1 | -1 | ||||||||||||
| y3 | |||||||||||||
| x2 | |||||||||||||
| y2 | -1 | -3 | |||||||||||
| F | |||||||||||||
| G | -1* | ||||||||||||
|
|
|
Продолжение Таблицы 3.1
| № | б.п. | x1 | x2 |
| y1 | y2 | z1 | z2 | y3 | y4 | y5 | b |
| y4 | -6 | -5 | ||||||||||
| x1 | -6 | -4 | ||||||||||
| y3* | -2 | |||||||||||
| x2 | ||||||||||||
| y2 | -15 | -1 | -10 | |||||||||
| F | -1* | |||||||||||
| G | ||||||||||||
| y4 | 1/3 | 1/3 | -4/3 | 29/3 | ||||||||
| x1 | 1/3 | 1/3 | -1/3 | 38/3 | ||||||||
|
| -1/9 | 1/18 | 11/18 | 11/18 | ||||||||
| x2 | 1/9 | -1/18 | 7/18 | 97/18 | ||||||||
| y2 | 4/3 | -1 | 5/6 | -5/6 | 241/6 | |||||||
| F | 1/9 | 1/9 | -1/9 | 1/18 | 11/18 | 11/18 |
|
|
|
