 |
Задача линейного программирования с нечеткой целевой функцией
|
|
|
|
при четких ограничениях 
где 
, 
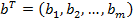– вещественные векторы; 
- вещественная матрица; 
- вектор коэффициентов целевой функции.
Пусть ЛПР может указать только интервалы значений коэффициентов целевой функции 
, и только один элемент из пространства 
, является истинным вектором коэффициентов целевой функции.
Исходная задача имеет единственную целевую функцию с бесконечным множеством векторов 
из ограниченного интервала 
, 
, 
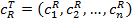, которые рассматриваются как параметры.
Определение всего множества эффективных решений сопряжено с большими вычислительными затратами. Вместо этого часто определяют так называемое «компромиссное» решение, для которого рассматривают различные функции предпочтения, преобразующие бесконечное множество целевых функций в единственную компромиссную функцию.
Самый простой способ – это выбрать единственного представителя 
для каждого интервала и перейти к решению ЗЛП вида:
,
используя стандартные алгоритмы.
При выборе подходящих компромиссных целевых функций исключают два крайних случая:
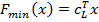и 
,
так как они отражают слишком пессимистическое и слишком оптимистическое суждения ЛПР. Для достижения компромиссного решения разумно выбрать в качестве представителя для каждого интервала значение с наибольшими шансами появления. Поскольку ЛПР не имеет достаточной информации, он часто выбирает середину интервала , получая целевую функцию вида:
.
В качестве развития этого варианта используется целевая функция, основанная на правиле Гурвица:
где 
– параметр оптимизма 
.
Другой способ построения компромиссной целевой функции заключается в выборе множества состояний «природы» 
как состояний неопределенности. При этом необходимо:
|
|
|
1) указать вероятности состояний 
;
2) определить для каждого состояния «природы» параметры настолько точно, насколько возможно.
Если выбранный представляющий вектор обозначить как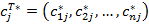 
, то ожидаемая величина
должна быть выбрана в качестве функции компромисса.
Например. Используя рассмотренный подход, решим следующую задачу.
и 
Предположим, что имеется три состояния «природы» 
с вероятностями 
, 
, 
, а соответствующие параметры состояния «природы» заданы так: 
. Проведем расчеты для параметра оптимизма 
и 
.
Алгоритм решения задачи включает следующую последовательность шагов.
1. Определим два крайних варианта компромиссных целевых функций, которые получают при максимальных и минимальных значениях коэффициентов.
;
.
2. Определим 
и 
, решая ЗЛП с исходными ограничениями.
при 
и 
при 
3. Определим компромиссную целевую функцию.
а) . 
=
Оптимальное решение для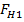 
при исходных ограничениях 
, 
.
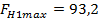б) . 
=
Оптимальное решение для 
при исходных ограничениях 
, 
.
4. Найдем ожидаемое значение целевой функции компромисса
,
, 
, 
.
Ожидаемая величина равна
= 
.
5. Решаем ЗЛП с целевой функцией 
и исходными ограничениями.
137,5 при .
Задачи и упражнения
1. Решить ЗНМП, с учетом вектора допустимых нарушений ограничений и целевой функции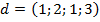 
:
2. Решить ЗНМП, с учетом вектора допустимых нарушений ограничений и целевой функции 
:
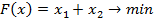
3. Решить ЗНМП, с учетом вектора допустимых нарушений ограничений и целевой функции 
:
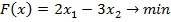
4. Решить ЗНМП, с учетом вектора допустимых нарушений ограничений и целевой функции 
:
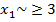
5. Решить ЗНМП с нечеткой целевой функцией:1) используя правило Гурвица с различными параметрами оптимизма; 2) учитывая распределение состояний «природы» 
и соответствующие параметры этих состояний 
и 
6. Решить ЗНМП с нечеткой целевой функцией:1) используя правило Гурвица с различными параметрами оптимизма; 2) учитывая распределение состояний «природы» 
и соответствующие параметры этих состояний 
|
|
|
и 
7. Решить ЗНМП с нечеткой целевой функцией:1) используя правило Гурвица с различными параметрами оптимизма; 2) учитывая распределение состояний «природы» 
и соответствующие параметры этих состояний 
и 
8. Решить ЗНМП с нечеткой целевой функцией:1) используя правило Гурвица с различными параметрами оптимизма; 2) учитывая распределение состояний «природы» 
и соответствующие параметры этих состояний 
и 
|
|
|
