Методы восстановления зависимостей

Наиболее широко в данной работе будут рассмотрены методы построения психодиагностических методик на базе интенсиональных методов, основанных на предположениях о классе решающих функций. Поэтому рассмотрим их более подробно.

Основным достоинством методов, основанных на предположении о классе решающих функций является ясность математической постановки задачи распознавания как поиска экстремума. Многообразие методов этой группы объясняется широким спектром используемых функционалов качества решающего правила и алгоритмов поиска экстремума. Обобщением данного класса алгоритмов является метод стохастической аппроксимации [94].

В данном классе алгоритмов распознавания образов содержательная формулировка задачи согласно [29] ставится следующим образом:

Имеется некоторое множество наблюдений, которые относятся к p различных классов. Требуется, используя информацию об этих наблюдениях и их классификациях, найти такое правило, с помощью которого можно было бы с минимальным количеством ошибок классифицировать вновь появляющиеся наблюдения.

Наблюдение задается вектором x, а его классификация - числом  ().

Таким образом, требуется, имея последовательность из l наблюдений и классификаций 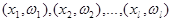 построить такое решающее правило , которое с возможно меньшим числом ошибок классифицировало бы новые наблюдения.

Для формализации термина «ошибка» принимается предположение о том, что существует некоторое правило , определяющее для каждого вектора x классификацию , которая называется «истинной». Ошибкой классификации вектора x с помощью правила  называется такая классификация, при которой  и  не совпадают.

Далее предполагается, что в пространстве векторов x существует неизвестная нам вероятностная мера (обозначаемая плотность ). В соответствии с   случайно и независимо появляются ситуации x, которые классифицируются с помощью правила . Таким образом определяется обучающая последовательность .

Качество решающего правила  записывается в виде , где .

Проблема следовательно заключается в построении решающего правила  таким образом, чтобы минимизировать функционал .

Сходной с задачей распознавания образов является задача восстановления регрессии, предпосылки к которой формулируются следующим образом:

Два множества элементов связаны функциональной зависимостью, если каждому элементу x может быть поставлен в соответствие элемент y. Эта зависимость называется функцией, если множество x - векторы, а множество y - скаляры. Однако существуют и такие зависимости, где каждому вектору x ставится в зависимость число y, полученное с помощью случайного испытания, согласно условной плотности . Иначе говоря, каждому x ставится в соответствие закон , согласно которому в случайном испытании реализуется выбор y.

Существование таких связей отражает наличие стохастических зависимостей между вектором x и скаляром и скаляром y. Полное знание стохастической зависимости требует восстановления условной плотности , однако, данная задача весьма трудна и на практике (например, в задачах обработки результатов измерения) может быть сужена до задачи определения функции условного математического ожидания. Эта суженная задача формулируется следующим образом: определить функцию условного математического ожидания, то есть функцию, которая каждому x ставит в соответствие число y(x), равное математическому ожиданию скаляра y: . Функция y(x) называется функцией регрессии, а задача восстановления функции условного математического ожидания - задачей восстановления регрессии.

Строгая постановка задачи такова:

В некоторой среде, характеризующейся плотностью распределения вероятности P(x), случайно и независимо появляются ситуации x. В этой среде функционирует преобразователь, который каждому вектору x ставит в соответствие число y, полученное в результате реализации случайного испытания, согласно закону . Свойства среды P(x) и закон  неизвестны, однако известно, что существует регрессия . Требуется по случайной независимой выборке пар  восстановить регрессию, то есть в классе функций  отыскать функцию , наиболее близкую к регрессии .

Задача восстановления регрессии является одной из основных задач прикладной статистики. К ней приводится проблема интерпретации прямых экспериментов.

Задача решается в следующих предположениях:

–Искомая закономерность связывает функциональной зависимостью величину y с вектором x: .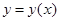

–Целью исследования является определение зависимости  в ситуации, когда в любой точке x может быть проведен прямой эксперимент по определению этой зависимости, то есть проведены прямые измерения величины . Однако вследствие несовершенства эксперимента результат измерения определит истинную величину с некоторой случайной ошибкой, то есть в каждой точке x удается определить не величину , а величину , где  - ошибка эксперимента, .

–Ни в одной точке x условия эксперимента не допускают систематической ошибки, то есть математическое ожидание измерения  функции в каждой фиксированной точке равно значению функции  в этой точке: .

–Случайные величины  и  независимы.

В этих условиях необходимо по конечному числу прямых экспериментов восстановить функцию 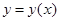. Требуемая зависимость есть регрессия, а суть проблемы состоит в отыскании регрессии по последовательности пар .

Задача восстановления регрессии принято сводить к проблеме минимизации функционала  на множестве  (интегрируемых с квадратом по мере 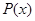 функций) в ситуации, когда плотность  неизвестна, но зато задана случайная и независимая выборка пар .