 |
Алгоритмы и методы безусловной оптимизации
|
|
|
|
Как было показано в предыдущем параграфе данной главы, решение основных задач восстановления зависимостей достигается при помощи процедуры оптимизации функционала качества.
Ее решение будет рассмотрено в подходах задачи безусловной минимизации гладкой функции 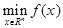 [77].
[77].
Данная задача непосредственно связана с условиями существования экстремума в точке:
* Необходимое условие первого порядка. Точка 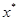 называется локальным минимумом
называется локальным минимумом  на
на  , если найдется
, если найдется  для
для  . Согласно теореме Ферма если
. Согласно теореме Ферма если  - точка минимума
- точка минимума 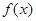 на
на 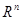 и
и  дифференцируема в
дифференцируема в  , то
, то  .
.
* Достаточное условие первого порядка. Если 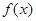 - выпуклая функция, дифференцируемая в точке
- выпуклая функция, дифференцируемая в точке  и
и  , то
, то  - точка глобального минимума
- точка глобального минимума  на
на 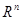 .
.
* Необходимое условие второго порядка. Если  - точка минимума
- точка минимума  на
на  и
и  дважды дифференцируема в ней, то
дважды дифференцируема в ней, то  .
.
* Достаточное условие второго порядка. Если в точке 
 дважды дифференцируема, выполнено необходимое условие первого порядка (
дважды дифференцируема, выполнено необходимое условие первого порядка ( ) и
) и  , то
, то  - точка локального минимума.
- точка локального минимума.
Условия экстремума являются основой, на которой строятся методы решения оптимизационных задач. В ряде случаев условия экстремума хотя и не дают возможности явного нахождения решения, но сообщают много информации об его свойствах.
Кроме того, доказательство условий экстремума или вид этих условий часто указывают путь построения методов оптимизации.
При обосновании методов приходится делать ряд предположений. Обычно при этом требуется, чтобы в точке  выполнялось достаточное условие экстремума. Таким образом, условия экстремума фигурируют в теоремах о сходимости методов.
выполнялось достаточное условие экстремума. Таким образом, условия экстремума фигурируют в теоремах о сходимости методов.
И, наконец, сами доказательства сходимости обычно строятся на том, что показывается, как «невязка» в условии экстремума стремится к нулю.
|
|
|
При решении оптимизационных задач существенны требования существования, единственности и устойчивости решения.
Существование точки минимума проверяется при помощи теоремы Вейерштрасса:
Пусть  непрерывна на
непрерывна на 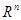 и множество
и множество  для некоторого
для некоторого  непусто и ограничено. Тогда существует точка глобального минимума
непусто и ограничено. Тогда существует точка глобального минимума  на
на  .
.
При анализе единственности точки экстремума применяются следующие рассуждения:
Точка минимума называется локально единственной, если в некоторой ее окрестности нет других локальных минимумов. Считается, что  - невырожденная точка минимума, если в ней выполнено достаточное условие экстремума второго порядка (
- невырожденная точка минимума, если в ней выполнено достаточное условие экстремума второго порядка ( ,
,  ).
).
Доказано, что точка минимума (строго) выпуклой функции (глобально) единственна.
Проблема устойчивости решения возникает в связи со следующим кругом вопросов:
* Пусть метод оптимизации приводит к построению минимизирующей последовательности, следует ли из этого ее сходимость к решению?
* Если вместо исходной задачи минимизации решается задача, сходная с ней, можно ли утверждать близость их решений?
В [77] приводится следующее определение устойчивости:
Точка  локального минимума
локального минимума  называется локально устойчивой, если к ней сходится любая локальная минимизирующая последовательность, то есть если найдется
называется локально устойчивой, если к ней сходится любая локальная минимизирующая последовательность, то есть если найдется  такое, что из
такое, что из  следует
следует  .
.
При обсуждении проблемы устойчивости решения задачи оптимизации можно выделить следующие важные теоремы.
* Точка локального минимума непрерывной функции 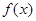 локально устойчива тогда и только тогда, когда она локально единственна.
локально устойчива тогда и только тогда, когда она локально единственна.
* Пусть  - локально устойчивая точка минимума непрерывной функции
- локально устойчивая точка минимума непрерывной функции  , а
, а  - непрерывная функция. Тогда для достаточно малых
- непрерывная функция. Тогда для достаточно малых  функция
функция  имеет локально единственную точку минимума
имеет локально единственную точку минимума 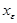 в окрестности
в окрестности  и
и  при
при  .
.
* Пусть  - невырожденная точка минимума
- невырожденная точка минимума  , а функция
, а функция  непрерывно дифференцируема в окрестности точки
непрерывно дифференцируема в окрестности точки  . Тогда для достаточно малых
. Тогда для достаточно малых  существует
существует  - локальная точка минимума функции
- локальная точка минимума функции 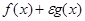 в окрестности
в окрестности  , причем
, причем 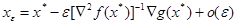 .
.
|
|
|
Помимо качественной характеристики точки минимума (устойчива она или нет) существенным является вопрос количественной оценки устойчивости. Такие оценки, позволяющие судить о близости точки  к решению
к решению  , если
, если 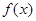 близко к
близко к  записываются следующим образом:
записываются следующим образом:
Для сильно выпуклых функций:
 ,
,
где  - константа сильной выпуклости.
- константа сильной выпуклости.
Для невырожденной точки минимума:
 ,
,
где  - наименьшее собственное значение матрицы
- наименьшее собственное значение матрицы  .
.
Как видно, в каждом из этих определений  играет роль характеристики «запаса устойчивости» точки минимума.
играет роль характеристики «запаса устойчивости» точки минимума.
Кроме  в качестве характеристики устойчивости точки минимума используют «нормированный» показатель
в качестве характеристики устойчивости точки минимума используют «нормированный» показатель  , называемый обусловленностью точки минимума
, называемый обусловленностью точки минимума  .
.
 ,
,
 .
.
Можно сказать, что  характеризует степень вытянутости линий уровня
характеризует степень вытянутости линий уровня  в окрестности
в окрестности  - «овражность» функции (чем больше
- «овражность» функции (чем больше  , тем более «овражный» характер функции).
, тем более «овражный» характер функции).
Наиболее важны в идейном отношении следующие методы безусловной оптимизации: градиентный и Ньютона.
Идея градиентного метода заключается в том, чтобы достигнуть экстремума путем итерационного повторения процедуры последовательных приближений начиная с начального приближения  в соответствии с формулой
в соответствии с формулой 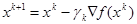 , где
, где  - длина шага.
- длина шага.
Сходимость данного метода подтверждается в доказательстве следующей теоремы:
Пусть функция  дифференцируема на
дифференцируема на  , градиент
, градиент  удовлетворяет условию Липшица:
удовлетворяет условию Липшица:
 ,
,
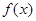 ограничена снизу:
ограничена снизу:

и  удовлетворяет условию
удовлетворяет условию
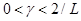 .
.
Тогда в градиентном методе с постоянным шагом 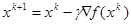 градиент стремится к 0:
градиент стремится к 0:  , а функция
, а функция  монотонно убывает:
монотонно убывает: 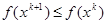 .
.
Для сильно выпуклых функций доказываются более сильные утверждения о сходимости градиентного метода.
При решении задачи оптимизации методом Ньютона используется подход, заключающийся в итерационном процессе вида
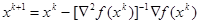
и в нахождении точки экстремума как решения системы из n уравнений с n неизвестными
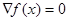 .
.
В методе Ньютона производится линеаризация уравнений в точке  и решение линеаризованной системы вида
и решение линеаризованной системы вида
 .
.
Анализ достоинств и недостатков итерационных методов оптимизации можно свести в таблицу (см. табл. 3).
| Таблица 3 Достоинства и недостатки итерационных методов оптимизации
|
|
|
Видно, что достоинства и недостатки этих методов взаимно дополнительны, что делает привлекательной идею создания модификаций этих методов, объединяющих достоинства методов и свободных от их недостатков.
Модификацией градиентного метода является метод наискорейшего спуска:
 ,
,  .
.
Модификация метода Ньютона с целью придания ему свойства глобальной сходимости возможна, например, способом регулировки длины шага:
 .
.
Такой метод называют демпфированным методом Ньютона. Возможные подходы к способу выбора шага  :
:
– Вычисление по формуле  ;
;
– Итерационный алгоритм, заключающийся в последовательном дроблении шага 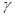 на константу
на константу 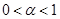 начиная со значения
начиная со значения 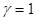 до выполнения условия
до выполнения условия  ,
,  или условия
или условия  ,
,  .
.
Демпфированный метод Ньютона глобально сходится для гладких сильно выпуклых функций.
Помимо одношаговых методов, к которым относятся градиентный метод и метод Ньютона, существует целый класс многошаговых методов, использующих для оптимизации информацию, полученную с предыдущих шагов. К ним относятся:
* Метод тяжелого шарика, использующий итерационную формулу 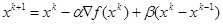 , где
, где  ,
,  - некоторые параметры. Введение инерции движения (член
- некоторые параметры. Введение инерции движения (член  ) в некоторых случаях приводит к ускорению сходимости за счет выравнивания движения по «овражистому» рельефу функции;
) в некоторых случаях приводит к ускорению сходимости за счет выравнивания движения по «овражистому» рельефу функции;
* Метод сопряженных градиентов. Здесь параметры оптимизации находятся из решения двумерной задачи оптимизации:
 ,
,
 .
.
Кроме всех вышеперечисленных методов оптимизации существует еще класс методов, основанных на идее восстановления квадратичной аппроксимации функции по значениям ее градиентов в ряде точек. К ним относятся:
* Квазиньютоновские методы, имеющие общую структуру  , где матрица
, где матрица  пересчитывается рекуррентно на основе информации, полученной на k-й итерации, так что
пересчитывается рекуррентно на основе информации, полученной на k-й итерации, так что  . К числу таких методов относятся ДФП (метод Давидона-Флетчера-Пауэлла) и BFGS или БФГШ (метод Бройдена-Флетчера-Гольдфарба-Шанно) [46].
. К числу таких методов относятся ДФП (метод Давидона-Флетчера-Пауэлла) и BFGS или БФГШ (метод Бройдена-Флетчера-Гольдфарба-Шанно) [46].
|
|
|
* Методы переменной метрики и методы сопряженных направлений, согласно которым метод  ,
, 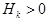 , может рассматриваться как градиентный в метрике
, может рассматриваться как градиентный в метрике  , а оптимальным выбором метрики является
, а оптимальным выбором метрики является  .
.
Нейронные сети
В данной работе задачи распознавания образов и восстановления зависимостей будут решаться в основном с применением нейронных сетей. Обзор данной темы основан на [1]-[6], [8]-[15], [22],[23], [32]-[34], [36]-[41], [59], [64], [67]-[70], [83]-[88].
Основные элементы
Нейронная сеть представляет собой структуру взаимосвязанных клеточных автоматов, состоящую из следующих основных элементов:
Нейрон - элемент, преобразующий входной сигнал по функции:

где x - входной сигнал, c - параметр, определяющий крутизну графика пороговой функции, а cm - параметр спонтанной активности нейрона.
Сумматор - элемент, осуществляющий суммирование сигналов поступающих на его вход:

Синапс - элемент, осуществляющий линейную передачу сигнала:

где w - “вес” соответствующего синапса.
Структура сети
Сеть состоит из нейронов, соединенных синапсами через сумматоры по следующей схеме:
|
|
|
|
|



 .
.
