 |
Запись решения в идеологии нейросетей
|
|
|
|
|
|
Как уже было сказано, выше, ряд вида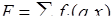 
может быть представлен как нейронная сеть, имеющая структуру, показанную на рис.1.
Тогда вычисление градиента функции ошибки H можно производить, используя схему, двойственную данной. При этом решение задачи может быть существенно упрощено применением следующего приема. Поскольку обучение следующего слоя начинается тогда, когда предыдущие уже обучены, а их связи зафиксированы, то, фактически, каждый нейрон обучается отдельно от других, а в качестве значения, вычисляемого k-м нейроном берется погрешность вычисления функции предыдущими k-1 - нейронами, или Fi.
Процесс обучения всей сети сводится этим ее разбиением к ряду последовательных процессов обучения структур вида, представленного на рис. 2.
|
|
Здесь x1 - xN - входные сигналы сети, Wij(1) - синапсы первого слоя от i-го входа к j-му сумматору первого слоя, Wj1(2) - синапсы второго слоя от j-го преобразователя к выходному сумматору, fj - j-й преобразователь, символом обозначаются тривиальные сумматоры.
Далее в тексте такая структура будет именоваться «потоком сети» или просто «потоком».
Вычисление производных H (функции ошибки) для сети, представляющего собой один «поток», можно вести на основе аппарата двойственных функций и алгоритма обратного распространения ошибки. Схема прохождения сигналов при обратном функционировании показана на рис. 3.
|
|
Здесь 
- двойственный сигнал от функции оценки, передаваемый без изменения через тривиальный сумматор второго слоя, 
- двойственный сигнал от соответствующего синапса второго слоя, 
- двойственный сигнал от преобразователя j-го «потока», передающийся сумматору для раздачи на синапсы, 
- двойственные сигналы соответствующих синапсов первого слоя.
|
|
|
Алгоритмическая часть
Обучение сети, состоящей из «потоков» производится в соответствии с алгоритмом, представленным на рис. 4.
Здесь H - значение оценки сети, накопленное по всему задачнику, - константа малости ошибки.
|
|
Для обучения каждого из потоков используется алгоритм, показанный на рис.5. Здесь Nф - общее число функций, по которому идет обучение, o - карта параметров сети, h0 - шаг оптимизации в начале цикла, s - градиент функции оценки H по обучаемым параметрам.
Используемое в алгоритме условие остановки формируется из двух подусловий, скомбинированных через «или»:
1. Число шагов оптимизации, во время которых 
превысило заранее заданную величину (при обучении использовалось значение Nsh=15), то есть сеть в данной конфигурации уже не может улучшить оценку;
2. Достигнуто заданное значение функции оценки 
, то есть сеть уже обучена.
|
|
|
|
|
|
|
|
При обучении одного потока используются процедуры подбора шага оптимизации - Increase (поиск шага в сторону возрастания, блок-схему см. на рис. 6), Decrease (поиск шага в сторону убывания, блок-схему см. на рис. 7) и Parabola (поиск оптимального шага по формулам параболического поиска блок-схему см. на рис. 8).
В процедурах используются следующие обозначения:
H(...) - функция оценки сети, накопленная по всему задачнику;
h1, h2, h3 - различные значения величины шага оптимизации, используемые при ее подборе;
W - величина шага в вершину параболы, проходящей через точки (h1, H1), (h2, H2), (h3, H3). Вычисляется по формуле:
H1, H2, H3 - значения функции ошибки, соответствующие смещению обучаемых параметров по направлению градиента на величину шага h1, h2 è h3.
Условие выпуклости комбинации h1,2,3, H1,2,3 определяется формулой
Если выражение истинно, то условие выпуклости выполнено.
|
|
|
Теперь, рассмотрев алгоритмы обучения сети, перейдем к описанию компонентов, структуры и функционирования сети.
|
|
|
