 |
Задачи для самостоятельного решения
|
|
|
|
Задача 1. Пусть А={1,2,3,4,5,6,7}; В={4,5,6,7,8,9,10}; С={2,4,6,8,10}; И={1,2,3,4,5,6,7,8,9,10}. Определить следующие множества: 1) АÈС; 2) АÇВ; 3) АÇ(ВÈС); 4) (АÇВ)ÈС; 5)  ; 6) АDВ; 7) А\ В.
; 6) АDВ; 7) А\ В.
Задача 2. Для каждого из приведенных ниже множеств используйте диаграммы Эйлера-Венна и заштрихуйте те ее части, которые изображают заданные множества:
1) А\(АÇВ); 2) (АÇВ)DС; 3) (АÇВ)È(ВÇС)È(АÇС); 4) (А\ В)È(В\ С).
Задача 3. Проиллюстрировать диаграммами Эйлера-Венна формулы:
1) (АÈВ)ÇС=(АÇС)È(ВÇС); 2) (АÇВ)ÈС=(АÈС)Ç(ВÈС);
3)А\(ВÈС)=(А\ В)Ç(А\С).
Задача 4. А={ х Î 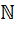 : 2< x £6}; В={ х Î
: 2< x £6}; В={ х Î 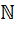 : 1< x £4}; С={ х Î
: 1< x £4}; С={ х Î 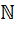 : x 2-4=0}.
: x 2-4=0}.
Определить следующие множества: 1) ВÈС; 2) АÇВÇС; 3) АÈВÈС.
Задача 5. Доказать формулы из задания №2, пользуясь принципом "Х£У и У£ХÞХ=У".
Отображение множеств
Если указан закон, сопоставляющий каждому элементу множества А некоторый элемент множества В, то говорят, что задано однозначное отображение f из А в В. Обозначается f: А®В.
Отображение f называется инъективным, если различные элементы множества А переходят в различные элементы множества В, то есть а 1¹ а 2Þ f (а 1)¹ f (а 2).
Отображение f называется сюръективным, если каждый элемент множества В имеет хотя бы один прообраз во множестве А, то есть для каждого b ÎВ существует а ÎА такой, что f(a)= b.
Если отображение инъективно и сюръективно, то оно называется биективным.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Пусть f:  определена таким образом: f(x)=3x+5.
определена таким образом: f(x)=3x+5.
Решение. 1. Отображение f инъективно, если f (а)= f (а '), то 3 а +5=3 а '+5, следовательно, а=а '. 2. Отображение f сюръективно для любого b Î  , требуется найти такое а, что f (a)= b = 3 a +5. Решая это уравнение относительно а, находим, что если а =1/3(b -5), тогда f(a)= b. Из 1. и 2. Þf – биективное отображение.
, требуется найти такое а, что f (a)= b = 3 a +5. Решая это уравнение относительно а, находим, что если а =1/3(b -5), тогда f(a)= b. Из 1. и 2. Þf – биективное отображение.
|
|
|
Задача 2. Пусть f:  определена таким образом: f(x)=x2+4.
определена таким образом: f(x)=x2+4.
Решение. 1. Отображение f не является инъективным, так как f(2)=f(-2)=8, но 2¹-2. 2. Отображение f не является сюръективным, так как не существует такого действительного числа а, для которого f(a)=-1. Из 1. и 2. следует, что f не является биективным отображением.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. РРрРРассмотрим отображение f:  . Выяснить, какие из приведенных ниже отображений являются инъективными, сюръективными: 1) f(x)=x4; 2) f(x)=3-x; 3) f(x)=x2-x3; 4) f(x)=x+x3; 5) f(x)=|x|; 6) f(x)=x3+6; 7) x+|x|.
. Выяснить, какие из приведенных ниже отображений являются инъективными, сюръективными: 1) f(x)=x4; 2) f(x)=3-x; 3) f(x)=x2-x3; 4) f(x)=x+x3; 5) f(x)=|x|; 6) f(x)=x3+6; 7) x+|x|.
Задача 2. На множестве людей L рассмотрим отображение f: L®L, сопоставляющее каждому человеку его мать. Является ли оно инъективным? Сюръективным?
Задача 3. На множестве точек плоскости рассмотрим отображение симметрии точки относительно начала координат. Будет ли оно инъективным? Сюръективным?
Задача 4. На множестве точек плоскости рассмотрим отображение проектирования точки на ось Ох. Является ли оно инъективным?
Мощность множества
Мощностью конечного множества А называется количество элементов в нем. Мощность принято обозначать card A .
Декартовым произведением множеств А и В называется множество АхВ, состоящее из всех упорядоченных пар {(а, b), а ÎА, b ÎВ}.
Правило произведения: для любых конечных множеств А и В card AxB=cardA×card B.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Заданы множества А{1,2}, В={3,4}. Выписать все элементы множества АхВ.
Решение. АхВ={(1,3),(1,4),(2,3),(2,4)}.
Задача 2. Верно ли, что мощность разности двух множеств равна разности их мощностей? В каких случаях это верно?
Решение. Рассмотрим множества А и В. card (A\B)=cardA\cardB верно в следующих случаях:
1. Если В=Æ, например, А={ a, b, c }, B=Æ. По определению А\В={ a,b,c }, card A=3, card B=0, card (A\B)=3. Итак, card (A\B)= card A - card В.
|
|
|
2. Если А£В, А={ a,b,c }, B={ a,b }, А\B={ с }Þ card (A\B)=1, card A - card B=3-2=1.
Итак, card (A\B)= card A - card B. Пусть А={ a,b,c }, В={ a,b,c }, А\В=ÆÞ card (A\B)=0. card A=3, card B=3. card A - card B=3-3=0. Итак, card (A\B)=0. card A - card B.
|
|
|


