 |
Совершенная конъюнктивная нормальная форма (СКНФ)
|
|
|
|
Существует и другая нормальная форма (конъюнктивная).
Выражение 
(отрицание на любых местах) называется элементарной дизъюнкцией (ЭД).
Конъюнкция нескольких ЭД называется конъюнктивной нормальной формой (КНФ).
Если к тому же все ЭД правильны и полны, то КНФ называется совершенной (СКНФ).
Рассмотрим способ получения СКНФ с помощью СДНФ.
Пусть дана булева функция f (x 1 … xn). Двойственной булевой функцией называется булева функция f *, заданная формулой
f *(x 1 … xn)= 
Заметим, что (f *)*= f.
Например, для f = x V y двойственной является f * = 
= xy.
Таким образом, двойственной к дизъюнкции является конъюнкция и наоборот.
Теорема (закон двойственности). Двойственная к композиции булевых функций есть соответствующая композиция двойственных булевых функций (композиция булевых функций – сложная функция, составленная из нескольких булевых функций).
Следствие 1. Если в формуле присутствует только дизъюнкция, конъюнкция и отрицания, то для получения достаточно заменить дизъюнкцию конъюнкцией и наоборот.
Следствие 2. Двойственной к СДНФ является СКНФ.
Из следствия 2 вытекает практический алгоритм преобразования данной формулы в СКНФ, используя двойственность:
1) найти f*;
2) преобразовать f* в СДНФ;
3) еще раз взять двойственную. (f *)*= f = СДНФ*=СКНФ.
Аналогично тому, как с помощью таблицы истинности была получена СДНФ, можно получить СКНФ. Для этого в последнем столбце таблицы выбираем нули, а в исходных наборах 0 заменим переменной, 1 – отрицанием переменной.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Найти двойственную функцию f * к функции f = x ®(y «
). f *= 
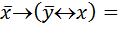x Ú(
.
Заметим, что двойственная функция к дизъюнкции является конъюнкцией с сохранением переменных и их отрицаний, и наоборот.
|
|
|
Задача 2. f =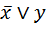 
. Найти f *.
Решение. f *=(x Ú 
)= 
.
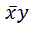Задача 3. Преобразовать СКНФ булеву функцию, заданную формулой (х Þ у)(z + x).
Решение. Действуем по алгоритму:
1. Находим f * =(х Þ у)(z + x)=(
f *= 
2. Преобразуем ее в СДНФ:
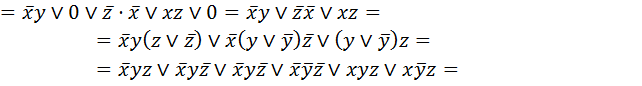
3. Еще раз возьмем двойственную:
f=(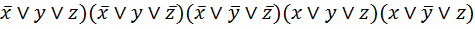 
.
Получили СКНФ, задача решена.
Найдем СКНФ данной функции с помощью таблицы истинности
| х | у | z | x ® y | z ®
| (x ® y)(z ® )
|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
В последнем столбце таблицы выберем нули. На исходных наборах 0 соответствует переменной, а 1 ее отрицанию, тогда СКНФ:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. Преобразовать в СКНФ булеву функцию, заданную формулой
а) f =( 
) (z® 
);
б) f = 
;
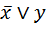в) f =( ) ®(z 
).
Задача 2. По таблице истинности получить СКНФ заданной булевой функции
а) f =(x 
) ®(z®t);
б) 
®(x 
).
Многочлены Жегалкина
Мы уже заметили, что конъюнкция совпадает с обычным арифметическим умножением, попробуем ввести сложение: 0+0=0; 0+1-1; 1+0=1; 1+1=? Если принять 1+1=1, то получим дизъюнкцию. Если принять 1+1=0, то получим исключающее или. Принимаем второе соотношение: х+у=хÅу. Такое сложение совпадает с известным в теории чисел сложением по модулю 2. Заметим, что всегда хÅх=0.
Всякая композиция сложений, умножений и констант называется арифметическим многочленом.
Многочленом Жегалкина называют многочлен вида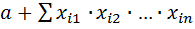 
, где суммирование ведется по некоторому множеству различных наборов (i1, i2,…,ik), в котором ни один индекс не повторяется.
Теорема. Всякая булева функция может быть представлена в виде многочлена Жегалкина и притом единственным образом.
Выразим три основные логические операции через сложение и умножение, превратив их в многочлены Жегалкина.
|
|
|
Конъюнкция хÙу=ху уже готовый многочлен Жегалкина. Отрицание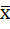 
=хÅ1. Дизъюнкция
=(xÅ1)(yÅ1)+1= xy Å x Å y Å1Å1= xy Å x Å y.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Преобразовать многочлен Жегалкина в булеву функцию, заданную формулой (хÞу)(z+х).
Решение. Последняя скобка уже является многочленом Жегалкина, поэтому преобразуем вначале только первую, затем раскрываем все скобки:
(хÞу)(z+х)= 
)(z+x)=((x+1)Úy)(z+x)=((x+1)y+x+1+y)(z+x)= =(xy+y+x+1+y)(z+x)=(xy+x+1)(z+x)=xyz+xyx+xz+xx+z+x=xyz+xy+xz++x+z+x=xyz+xy+xz+z.
|
|
|
