 |
Задачи для самостоятельного решения
|
|
|
|
Задача 1. Найти код Харари графа.
Задача 2. Восстановить граф по числу а) 527; б) 784; в) 956 как по коду Харари.
Задача 3. Существует ли граф с кодом Харари 282?
Деревья и ордеревья. Префиксный код бинарного
ордерева. Код Прюфера
Связный граф без циклов называется деревом.
не дерево
дерево
Орграф называется ордеревом с корнем х0, если:
1) в вершину х0 не заходит ни одна дуга;
2) в остальные вершины заходит единственная дуга;
3) граф не содержит контуров.
Ордерево называют бинарным, если каждая вершина имеет не более двух потомков.
Префиксный код бинарного ордерева
Каждой вершине будем сопоставлять двоичное число (двоичную строку). Корню ничего не сопоставляем, его левому потомку – 0, правому – 1. Потомкам 0 сопоставляем 00 и 01, а потомкам 1-10 и 11 и т.д.
Оказалось, что достаточно хранить двоичные строки не для всех вершин, а только для висячих (не имеющих потомков) {00;010;110}. Это и есть префиксный код бинарного дерева. Он определяет ордерево однозначно.
Код Прюфера
Пусть дано дерево или ордерево с n пронумерованными вершинами. Действуем по алгоритму:
1. В списке всех вершин 1..2..3..n слева направо ищем первую висячую вершину. Обозначим ее номер а1.
2. Вершина а1, будучи висячей, смежна с единственной вершиной b1, которую заносим в новый список – будущий код Прюфера, а вершину а1 удаляем и из списка и, из дерева.
3. Повторяем шаги 1,2 n-2 раза. Заметим, что дерево все время уменьшается и в нем иногда возникают новые висячие вершины.
|
|
|
4. В итоге получаем новый список {b1,b2,…,bn-1} – код Прюфера. Он определяет дерево однозначно (в ордереве на последнем шаге может возникнуть два варианта).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Восстановить и нарисовать бинарное ордерево по префиксному коду {00,010,110,11}.
Решение. Наибольшая длина двоичной строки равна трем, следовательно, глубина ордерева также равна трем. Так как в префиксном коде указаны только висячие вершины, то по ним и восстанавливаем ордерево
| 0 |
| 1 |
| 110 |
| 01 |
| 010 |
| 00 |
| 11 |
Задача 2. Построить код Прюфера для дерева
Решение.
| 7 |
| 8 |
| 2 |
| 5 |
| 3 |
| 1 |
| 4 |
| 6 |
| 9 |
Задача 3. Восстановить дерево по коду Прюфера {1,1,4,1,6,2}
Решение. Число символов в коде n-2=6, значит, у дерева n=8 вершин. Наименьшим из номеров, не входящих в код, является 3, значит, вершина 3 инцидентна вершине 1. Вычеркиваем 3 из списка вершин и просматриваем список дальше. Наименьшим из оставшихся и не входящих в код номеров является 5. Вершина 5 инцидентна вершине 1.
1 2 3 4 5 6 7 8 3«1.
1 2 3 4 5 6 7 8 5«1.
Продолжаем процесс:
1 2 3 4 5 6 7 8 7«4
(вершина 4 становится висячей).
1 2 3 4 5 6 7 8 4«1
(вершина 1 становится висячей).
1 2 3 4 5 6 7 8 1«6
(вершина 6 становится висячей).
1 2 3 4 5 6 7 8 6«2.
Изобразим дерево
| 5 |
| 3 |
| 1 |
| 6 |
| 2 |
| 8 |
| 4 |
| 7 |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. Восстановить бинарное ордерево по префиксному коду: а) {001,010,011,1000,1010,110,1111}; б) {00,010,011,101,11}; в) {001,101,1101,111}.
|
|
|
Задача 2. Написать код Прюфера для данного дерева:
| 1 |
| 1 |
| 4 |
| 5 |
| 6 |
| 2 |
| 7 |
| 4 |
| 8 |
| 2 |
| 6 |
| 9 |
| 11 |
| 3 |
| 8 |
| 10 |
| 7 |
| 3 |
| 5 |
| 9 |
Задача 3. Восстановить дерево по коду Прюфера: а) {2,2,4,4,3,6,2,3}; б) {3,1,2,2,1,4,4,3,3,5,1}; в) {2,3,6,6,2,7,2,6,3}.
Обход дерева. Понятие списка. Деревья и списки
Часто необходимо обойти все вершины большого дерева не хаотически, а по определенному алгоритму. Для бинарных ориентированных деревьев существует три канонических способа обхода.
1. Прямой (КЛП – корень, лево, право). Сначала мы учитываем корень, затем левое поддерево и правое поддерево. Это правило выполняется для каждой вершины, начиная с корня.
2. Обратный (ЛКП – лево, корень, право). Сначала мы учитываем левое поддерево, затем корень и правое поддерево. Это правило выполняется для всех вершин, начиная с корня.
3. Концевой (ЛПК – лево, право, корень). Сначала мы учитываем левое поддерево, затем правое и корень.
Введем понятие атома. Атом – некоторый неделимый объект (буква, цифра и т.д.). Атомам соответствуют висячие вершины ордерева. Число вершин первого уровня является длиной списка. Причем, верно и обратное, что каждому дереву можно сопоставить список его висячих вершин.
Списком называется последовательность атомов и списков, заключенных в скобки и разделенных запятыми. Глубиной списка называется глубина дерева.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Обойти тремя способами бинарное дерево
| 11 |
| 8 |
| 7 |
| 6 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 9 |
| 10 |
Решение. 1. Прямой (КЛП). 1 2 4 5 8 3 6 9 7 10 11.
2. Обратный (ЛКП) 4 2 8 5 1 6 9 3 1 0 7 1 1.
3. Концевой (ЛКП) 4 8 5 2 9 6 1 0 1 1 7 3 1.
Задача 2. Нарисовать дерево, соответствующее списку:
а) (а); б) (а,b,с); в) (а,(b,с), (е,(f,k))).
Решение.
а) б) с)
| k |
| f |
| е |
| с |
| b |
| а |
| а |
|
|
|
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. Обойти тремя способами бинарное ордерево.
| a |
| e |
| l |
| m |
| k |
| d |
| q |
| f |
| c |
| b |
| а |
| n |
| p |
| m |
| l |
| b |
| e |
| f |
| d |
| c |
| k |
Задача 2. Нарисовать дерево, соответствующее списку
а) (а,(b,(c,d)), (e,f),k);
б) (а,(b,(c,(d,e))), (k(l,m)),p);
в) ((a,b), (c,(d,e),(f,k))).
Задача 3. Написать список висячих вершин данного ордерева
а) б)
| t |
| l |
| m |
| k |
| s |
| p |
| m |
| b |
| e |
| f |
| d |
| c |
| a |
Задача 4. Найти глубину списка.
а) ((a,(b,(c,d))), (f,e),k); б) (a,(b,(c,(d,k))), (e,(f,((q,m),h)))).
ТЕМА 3. БУЛЕВЫ ФУНКЦИИ
Булевой функцией y = f (x 1, x 2,…, x n) от n переменных x 1, x 2,…, x n называется любая функция, в которой аргументы и функция могут принимать значение либо 0, либо 1, т.е. булева функция это правило, по которому по произвольному набору нулей и единиц (x 1, x 2,…, x n) ставится в соответствие значение 0 или 1.
Вектором значений булевой функции у = f (x 1, x 2,…, x n) называется упорядоченный набор всех значений функции f, при котором значения упорядочены по лексикографическому порядку.
Среди булевых функций особо выделяются так называемые элементарные булевы функции, посредством которых можно описать любую булеву функцию от любого числа переменных.
1. Булева функция f (x 1, x 2,…, x n), принимающая значение 1 на всех наборах нулей и единиц, называется константой 1, или тождественной единицей. Обозначение: 1.
2. Булева функция f (x 1, x 2,…, x n), принимающая значение 0 на всех наборах нулей и единиц, называется константой 0, или тождественным нулем. Обозначение: 0.
3. Отрицанием называется булева функция одной переменной, которая определяется следующей таблицей истинности
| х | 0 | 1 |
| f(x) | 1 | 0 |
Обозначения: Ø х, 
. Запись Ø х читается «не икс» или «отрицание икс».
4. Конъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 0 | 0 | 0 | 1 |
Другие названия: логическое умножение (произведение); логическое «и».
|
|
|
Обозначения: х × у, х Ù у, min (x, y). Запись может читаться так: «икс и игрек» или «икс умножить на игрек».
5. Дизъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 0 | 1 | 1 | 1 |
Другие названия: логическое сложение (сумма); логическое «или». Обозначение: хÚу, max (x, y).
Запись хÚу может читаться так: «икс или игрек» или «сумма икс и игрек».
6. Импликацией называется булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 1 | 1 | 0 | 1 |
Другое название: логическое следование.
Обозначения: х®у, хÞу, хÉу. Запись х®у может читаться так: из икс следует игрек».
7. Эквивалентностью называется булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 1 | 0 | 0 | 1 |
Обозначения: х ~ у, х «у, х º у.
Запись х ~ у может читаться так: «икс эквивалентно игрек» или «икс равносильно игрек».
8. Суммой по модулю_2 называется булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 0 | 1 | 1 | 0 |
Другое название: антиэквивалентность.
Обозначения: х Å у, х+у.
Запись х Å у может читаться так: «икс плюс игрек».
9. Штрих Шерифа это булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 1 | 1 | 1 | 0 |
Другое название: отрицание конъюнкции, логическое «не-и».
Обозначение: х | у.
Запись х | у может читаться так: «не икс или не игрек», «икс и игрек несовместны», «икс штрих Шеффера игрек».
10. Стрелка Пирса это булева функция двух переменных, которая определяется следующей таблицей истинности
| x | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 |
| f(x,y) | 1 | 0 | 0 | 0 |
Другое название: отрицание дизъюнкции, логическое £ не - или ³.
Обозначение: х ¯ у.
Все логические операции можно выразить через три логические операции (конъюнкция, дизъюнкция, отрицание).
Применение логических операций и функций определяются скобками. Если скобок нет, то логические операции применяются в следующей последовательности: отрицание, дизъюнкция, конъюнкция, импликация, эквиваленция.
Определение. Две функции f 1 (x 1, …, x n) и f 2 (x 2, …, x n) называются равносильными, если они принимают одинаковое значение на одних и тех же наборах переменных. Функция от f 1 (x 1, …, x n) называется тождественно-истинной, если она принимает значения 1 на всех наборах своих переменных. Функция f 1 (x 1, …, x n) называется тождественно-ложной если она принимает значение 0 на всех своих наборах переменных.
|
|
|
Рассмотрим 3 основные группы равносильности.
1. Основные равносильности
· 
;
· 
;
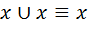· x* 1º x;
· 
;
· x* 0º0;
· 
;
· x * 
;
· 
;
· 
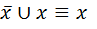(закон двойного отрицания);
· 
(закон поглощения);
· 
(закон поглощения).
2. Равносильности, выражающие одни логические операции другими
· 
;
· 
;
· 
;
· 
;
· 
;
· 
;
· 
.
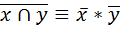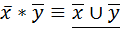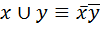3. Равносильности, выражающие основные законы алгебры и логики
· 
;
· 
;
· 
;
· 
;
· 
;
· 
.
Для того чтобы сравнить две булевых функции, удобно привести их к некоторому стандартному виду.
|
|
|
