 |
Выборочные характеристики и их свойства. Нормальное распределение и его характеристики.
|
|
|
|
Порядок проведения сертификации услуг.
Сертификация услуг включает следующие этапы:
1. Подача заявителем Заявки на проведение сертификации услуги в орган по сертификации;
2. Рассмотрение Заявки и принятие Решения о возможности проведения сертификации. Орган по сертификации рассматривает заявку и в кратчайшие сроки, но не позднее одного месяца после её получения, сообщает заявителю решение. Решение органа по сертификации может быть как положительным, так и отрицательным.
3. Оценка соотв-ия работ и услуг установленным требованиям согласно схеме сертификации;
4. Принятие решения о возможности выдачи сертификата. Орган по сертификации анализирует документы о соответствии услуг установленным требованиям. Результаты этой оценки отражают в заключении эксперта. На основании данного заключения орган по сертификации принимает Решение о выдаче сертификата (или отказывает в выдаче, если хотя бы по одному показателю услуга не соответствует установленным требованиям), оформляет сертификат и регистрирует его.
5. Выдача сертификата и лицензии на применение знака соотв-ия. Сертификат действителен только при наличии регистрационного номера. В сертификате при заполнении указываются все документы, служащие основанием для его сертификата, в соответствии со схемой сертификации. Держатель сертификата соответствия получает право маркирования документации на сертифицированные услуги знаком соответствия на основе лицензии на применение знака соответствия. Лицензиянаприменениезнакасоответствия - документ, выданный уполномоченным органом, посредством которого держателю сертификата соответствия предоставляется право применятьзнаксоответствия в пределах, установленных этим документом.
|
|
|
6. Инспекционный контроль сертифицированных работ и услуг. Инспекционный контроль за сертифицированной услугой проводится в течение всего срока действия сертификата и лицензии не реже одного раза в год в форме периодических и внеплановых проверок. Инспекционный контроль необходим для того, чтобы подтверждать, что предоставляемые услуги продолжают соответствовать установленным требованиям, подтверждённым при сертификации. По результатам инспекционного контроля орган по сертификации может приостановить или отменить действие сертификата и аннулировать лицензию на право применения знака соответствия в случае несоответствия предоставляемой услуги требованиям нормативных документов.
Выборочные характеристики и их свойства. Нормальное распределение и его характеристики.
Выборочные характеристики их свойства:
Выборкой называется часть данных, полученных из общей совокупности называемой генеральной. Если выборка хорошо представляет соответствие характеристики ее называют представительной или репрезентативной.
Ранжирование – упорядочение данных по возрастанию или убыванию. Для получения статистического ряда необходимо ранжирование и объединение одних и тех же значений в группы.
Дискретное измерение случайной величины – если рядом стоящие значения в ранжированном ряду отличаются друг от друга на некоторую конечную величину (на целое число) (количество бракованных изделий).
Непрерывное изменение случайной величины – если значения в ранжированном ряду отличаются друг от друга на сколь угодно малую величину (измерение, массы, диаметра).
СА величина – сумма значений рассматриваемой величины, полученных по результатам испытаний выборки, деленная на её объем: 
= 
(х1+х2+…+хn) = 
Средневзвешенная величина: = 
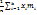n =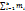 
|
|
|
Медиана -значение параметра, которое делит упорядоченный ряд на 2 равные по объему группы.
Ме = Xi- для нечетного ряда
Ме = (Xi + Xi+1)/2 - для четного числа измерений
Например:
а) Четный ряд 1 1 3 2 1 4
1 1 (1 2) 3 4 (ранжируем)
(1+2)/2 Ме = 1,5
б) Нечетный ряд 1 1 3 2 1 4 5
1 1 1 (2) 3 4 5 (ранжируем) Ме = 2
Размах (R) –разница между max и min значениями в выборке: R = Xmax - Xmin
Выборочная дисперсия – мера рассеяние случайной величины. Оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию несмещённую или исправленную.
S2= 
.
Вместо S2 часто применяют выборочное стандартное отклонение (СКО) - положительный квадратный корень из выборочной дисперсии. Оно показывает насколько выборочные значения разбросаны относительно среднего. S=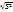 
Коэффициент вариации – отношение стандартного отклонения к СА, выраженному в %.V = (
)* 100%.
Характеристикой положения генеральной совокупности является мат.ожидание:
μ =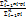 
xi – дискретные значения случайной величины; pi – соответствующие им вероятности.
СКО мат.ожидания для генеральной совокупности: σ(х)2 =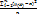 
Если технологический процесс отлажен и контролируется, то распределение параметров качества стремится к гауссовскому закону (нормальному закону), его легко узнать по колоколообразной форме. Нормальное распределение (гауссовское распределение или распределение Гаусса) — распределение вероятностей, которое задается функцией плотности распределения: f(x) =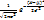 
. Нормальное распределение имеет 2 параметра μ (среднее значение (математическое ожидание) случайной величины, указывает координату максимума кривой плотности распределения) и σ² (дисперсия).
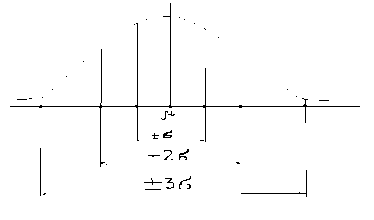
Площадь ±σ = 0,6825; ± 2σ = 0,9544; ± 3σ = 0,9973
Теоретически нормальная переменная может принимать любое значение от -∞ до +∞, но из рисунка видно, что уже для ± 3σ вероятность составляет 99,73%. Этот факт представляет собой важное правило нормального распределения – правило трех сигм.
|
|
|
