 |
Технологии операции с векторами
|
|
|
|
Операции с массивами в табличном процессоре
Массив – это набор данных одного типа. Массив в MS Excel хранятся в диапазоне ячеек. MS Excel позволяет создавать одномерные, двумерные и трехмерные массивы, которые хранятся соответственно в одномерных, двумерных и трехмерных диапазонах.
Одномерный и двумерный диапазоны создаются на одном рабочем листе. Адресная ссылка на такой диапазон имеет формат: <Адрес первой ячейки>:<Адрес последней ячейки>.
Трехмерные диапазоны создаются в одноименных ячейках нескольких смежных листов. Адресная ссылка на такой диапазон имеет формат: <Имя первого рабочего листа>:<Имя последнего рабочего листа>!<Адрес первой ячейки>:<Адрес последней ячейки>, например: =’Лист1:Лист2’!$А$1:$В$4.
Если массив содержит данные арифметического типа, то с таким массивом можно выполнять арифметические операции, в которых в качестве операндов участвуют:
- массив и единственная переменная, например умножение элементов массива на число;
- двумерный массив и одномерный массив, например почленно-построчное умножение;
- массивы одинаковой размерности.
Для умножения (деления, сложения или вычисления функции) каждого элемента массива на число следует выполнить следующие действия:
- ввести значения элементов массива в ячейки рабочего листа;
- выделить область для размещения результата операции, ее размерность должна быть такой же, как размерность исходного массива;
- в строку формул ввести формулу, например = А1:В2*3;
- указать, что производится операция над массивом, нажав комбинацию клавиш <Ctrl>+<Shift>+<Enter>
Пример 1. Требуется умножить элементы массива размерностью 2 х 2 на число 3. Исходный массив 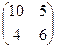 .
.
|
|
|
Решение:
Ввести в ячейки диапазона значения элементов массива.
Выделить диапазон ячеек такой же размерности, в который будет помещаться результат операции.
Ввести в выделенный диапазон формулу в формате: =Адрес начальной ячейки диапазона: Адрес конечной ячейки диапазона * Адрес второго операнда.
Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>. В ячейках выделенного диапазона появится результат (Рисунок 1).
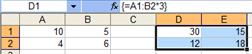
Рисунок 1
Технологии операции с векторами
2.1. Вычисление суммы векторов
Вектора и матрицы в электронной таблице хранятся в виде массивов.
Сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов: 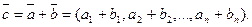
Для вычисления суммы векторов необходимо выполнить следующую последовательность действий:
- в диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
- выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы;
- ввести в выделенный диапазон формулу перемножения диапазонов = Адрес вектора 1 * Адрес вектора 2;
- нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Пример 2. Даны два вектора: 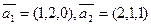 . Требуется вычислить сумму этих векторов.
. Требуется вычислить сумму этих векторов.
Решение:
В ячейки диапазона А2:А4 ввести значения координат вектора  , а в ячейки диапазона С2:С4 – координаты вектора
, а в ячейки диапазона С2:С4 – координаты вектора  .
.
Выделить ячейки диапазона, в которых будет вычисляться результирующий вектор  (Е2:Е4) и ввести в выделенный диапазон формулу = А2:А4+С2:С4.
(Е2:Е4) и ввести в выделенный диапазон формулу = А2:А4+С2:С4.
Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>. В ячейках диапазона Е2:Е4 будут вычислены соответствующие координаты результирующего вектора (Рисунок 2).
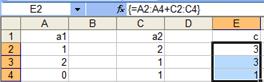
Рисунок 2
2.2. Вычисление произведения вектора на число
Произведением вектора на число является вектор, координаты которого получаются умножением соответствующих координат исходного вектора на это число: 
Для вычисления произведения вектора на число необходимо выполнить следующую последовательность операций:
|
|
|
- в диапазон ячеек рабочего листа ввести числовые значения элементов вектора;
- в ячейку ввести значение числа, на которое нужно умножить вектор;
- выделить диапазон ячеек той же размерности, что и исходный вектор для вычисляемого результата;
- ввести в выделенный диапазон формулу перемножения: Адрес вектора 1 * Адрес числа;
- нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
2.3. Вычисление скалярного произведения векторов
Скалярное произведение векторов – это сумма произведений соответствующих координат этих векторов: 
Для вычисления скалярного произведения векторов необходимо применить следующую последовательность операций:
- в диапазон ячеек одинаковой размерности ввести значения числовых элементов каждого вектора;
- выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные диапазоны;
- ввести в выделенный диапазон формулу перемножения диапазонов:
= СУММ (Адрес вектора 1 * Адрес вектора 2).
Пример 3. Даны два вектора 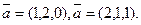 Требуется вычислить произведение этих векторов.
Требуется вычислить произведение этих векторов.
Решение:
В ячейки диапазона А2:А4 ввести значения координат вектора  , а в ячейки диапазона С2:С4 – координаты вектора
, а в ячейки диапазона С2:С4 – координаты вектора  .
.
В ячейку, в которой нужно получить результат Е2 ввести формулу =СУММ(А2:А4*С2:С4) и нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>. В результате вычисления будет получен результат – 4 (Рисунок 3).
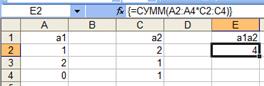
Рисунок 3
|
|
|


