 |
Применение технологий при решении экономических задач
|
|
|
|
5.1. Применение технологий при решении микроэкономических задач
Пример 9. Предприятие ежесуточно выпускает четыре вида изделий, их производственно-экономические показатели приведены в Таблице 2.
Таблица 2.
| Вид изделия. Условный номер | Количество выпускаемых изделий, шт. | Расход сырья, кг/изд. | Норма времени изготовления ч/изд. | Стоимость изделия, ден.ед/изд. |
| N | s | t | p | |
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Решение:
Приведенные в Таблице 2 производственно-экономические показатели можно представить в виде следующих векторов: 
= (20 50 30 40) – вектор количества выпускаемых изделий по видам продукции; 
= (5 2 7 4) – вектор расхода сырья по видам продукции; 
= (10 5 15 8) – вектор затрат времени на изготовление продукции; 
= (30 15 45 20) – вектор стоимости. Тогда решение задачи будет представлять собой скалярные произведения вектора количества выпускаемой продукции на три других вектора: ежесуточны расход сырья S будет вычисляться по формуле S = , затраты рабочего времени Т – по формуле Т = , стоимость выпускаемой продукции Р = (Рисунок 10).
Рисунок 10
Пример 10. Предприятие выпускает три вида продукции из сырья трех типов. Характеристики производства приведены в Таблице 3.
Требуется определить возможный объем выпуска каждой продукции при заданных запасах сырья.
Таблица 3.
| Вид сырья | Расход сырья по видам продукции, вес. ед./изд. | Запас сырья, вес. ед. | ||
|
|
|
Решение:
Ввести обозначения неизвестных объемов выпускаемой продукции: х1, х2, х3. Тогда при условии полного расхода запасов сырья и при условии отсутствия ограничений, которые определяются другими ресурсами, балансовые соотношения можно записать в виде следующей системы уравнений:
.
Матрица системы и матрица свободных членов будут соответственно равны
, 
.
Количество уравнений в системе равно количеству неизвестных, поэтому для ее решения необходимо применить метод обратной матрицы. Решение приведено на Рисунке 11.
Рисунок 11
5.2. Применение технологий при решении макроэкономических задач
Известно, что рациональное функционирование многоотраслевого хозяйства предполагает соблюдение баланса между отраслями. Каждая отрасль многоотраслевого хозяйства является, с одной стороны, производителем определенной продукции, а с другой – потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями.
Балансовый принцип связи различных отраслей состоит в том, валовой выпуск i -й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид
xi = xi1 + xi2 + … + xin + yi, i = 1, 2, …, n, xi – общий объем выпускаемой продукции i- й отрасли; xij – объем продукции i -й отрасли, потребляемый j -й отраслью при производстве объема продукции xj; yi – объем продукции i -й отрасли конечного потребления (для реализации в непроизводственной сфере).
Для производства продукции j -й отрасли объемом xi нужно использовать продукцию i -й отрасли объемом aijxi, где aij – постоянное число, характеризующее прямые затраты. Это допущение позволяет представить модель многоотраслевой экономики (модель Леонтьева) в виде системы линейных уравнений, которая в матричной форме имеет вид 
,
|
|
|
где 
- вектор валового выпуска;
- вектор объема продукции конечного потребления;
А – матрица коэффициентов прямых затрат.
Приведенная система уравнений может быть представлена в виде 
,
где Е – единичная матрица.
Если существует обратная матрица (Е – А)-1 (матрица полных затрат), то существует единственное решение системы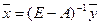 
.
Из экономической теории известно несколько критериев продуктивности матрицы А:
- матрица А продуктивна тогда и только тогда, кода матрица (Е – А)-1 существует и ее элементы неотрицательны;
- матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не больше единицы, причем хотя бы для одного столбца (строки) строго меньше единицы.
Пример 11. В Таблице 4 приведены данные по балансу за некоторый период времени между пятью отраслями.
Таблица 4.
| № п/п | Отрасль | Потребление | Конечный продукт | Валовой выпуск, ден. ед. | ||||
| Станкостроение | ||||||||
| Энергетика | ||||||||
| Машиностроение | ||||||||
| Автомобильная промышленность | ||||||||
| Добыча и переработка углеводородов |
Требуется найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить ее продуктивность.
В приведенной таблице в первых пяти столбцах (группа «Потребление») содержатся значения xij, в последнем столбце содержатся элементы вектора валового выпуска , в предпоследнем столбце – элементы вектора объема конечного потребления .
Решение:
В диапазон ячеек рабочего листа (B4:F8) ввести числа (Рисунок 12), записанные в столбцах «Потребление» Таблицы 4.
Ввести в ячейки диапазона (Н4:Н8) значения элементов вектора валового выпуска Х, который соответствует последнему столбцу Таблицы 4, а в диапазон (I4:I8) – значения элементов вектора Y – вектор конечного продукта.
Рисунок 12
Матрица коэффициентов прямых затрат А вычисляется путем деления i -го столбца матрицы «Потребление» на i -ю строку вектора Х. Это вычисление можно выполнить, используя формулу А=П:ХТ, где П – матрица «Потребление».
|
|
|
Выделить диапазон ячеек (B11:F15), в котором будет размещаться матрица А и ввести в него формулу деления массива «Потребление» на транспонированный вектор Х: = B4:F8/ТРАНСП(Н4:Н8) и нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>. После выполнения этой операции в выделенном диапазоне будут вычислены значения элементов матрицы коэффициентов прямых затрат (Рисунок 13).
Просуммировать столбы полученной матрица А (Рисунок 13).
Вычислить значения элементов матрица полных затрат. Для этого выделить диапазон (B18:F22) и ввести в него формулу =МОБР(H11:L15-B11:F15).
Проанализировать полученные в результате расчетов данные.
Матрица полных затрат (Е – А)-1 существует, все ее элементы положительны. Следовательно, первое условие продуктивности матрицы А выполняется.
Все элементы матрица А положительные, однако в третьем и четвертом столбцах их суммы превышают значение единицы, следовательно второе условие продуктивности матрицы А не выполняется. Таким образом, матрица коэффициентов прямых затрат в решаемой задаче непродуктивна.
Рисунок 13
|
|
|
