Решение систем линейных уравнений

4.1. Метод обратной матрицы

Система m линейных уравнений с n неизвестными х₁, х₂, …, х_n имеет вид

Здесь a_ij и b_i – заданные числа, которые называются соответственно коэффициентами при неизвестных и свободными членами.

Для того чтобы представить систему линейных уравнений в матричном виде, коэффициенты при неизвестных представляют в виде матрицы

.

Матрица А называется матрицей системы.

Свободные и неизвестные члены представляются в виде матриц-столбцов

.

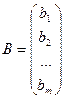
В матричной форме система линейных уравнений записывается в виде А х Х = В.

В частном случае, когда число уравнений в системе (m) равно числу неизвестных (n), т.е. m = n, то решение такой системы можно найти методом обратной матрицы в виде х = А^-1 х В, где А^-1 – матрица, обратная по отношению к исходной матрице А.

Пример7. Система уравнений задана матрицами , . Требуется решить заданную систему линейных уравнений.

Решение:

Присвоить диапазону А3:В4 имя (например, А) и ввести в ячейки значения элементов матрицы А.

Присвоить диапазону D3:D4 имя (например, В) и ввести значения элементов вектора В.

Выделить область F3:F4 для помещения результата решения системы и ввести в него формулу

=МУМНОЖ(МОБР(А);В).

Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>, в ячейках диапазона F3:F4 будет получен результат (Рисунок 7).

Рисунок 7

 

Чтобы выполнить проверку полученных результатов, достаточно перемножить исходную матрицу на вектор результата, итогом этой операции является массив, содержащий такие же значения, как вектор В.

При решении некоторых задач в электронной таблице в формулах удобно использовать ссылки на имена ячеек или диапазонов. Имя – это идентификатор. Область действия имени – вся рабочая книга. Для присвоения имени диапазону можно применить два приема:

- выделить диапазон и в поле имени записать идентификатор;

- выполнить команду меню Вставка – Имя – Присвоить. В открывшемся окне в поле Имя ввести идентификатор имени, а в поле Формула записать адрес диапазона.

 

4.2. Метод наименьших квадратов

В общем случае m может быть не всегда равно n. Возможны три случая: m<n, m=n, m>n. При m<n, если система является совместной, то она не определена и имеет бесконечное множество решений.

В случае если m>n и система совместна, то матрица А имеет по крайней мере m-n линейно независимых строк. В этом случае решение может быть получено отбором n любых линейно независимых уравнений и применением формулы х = А^-1 х В. Однако при решении задачи в электронной таблице удобнее применить более общий подход – метод наименьших квадратов. Для этого обе части уравнения нужно умножить на транспонированную матрицу системы А^Т: А^ТАХ = А^ТВ.

Затем обе части уравнения нужно умножить на (А^ТА)^-1. Если эта матрица существует, то система определена. С учетом того, что (А^ТА)^-1 х А^ТА = Е, где Е – единичная матрица, решение системы будет иметь вид Х = (А^ТА)^-1 х А^ТВ.

Пример 8. Требуется решить систему уравнений:

Решение:

Ввести значения элементов матрицы А в диапазон ячеек рабочего листа (А2:В4).

Ввести значения элементов вектора В в ячейки рабочего листа, например D2:D4.

Транспонировать исходную матрицу, для чего выделить диапазон ячеек размерностью 3 х 2 (А6:С7), ввести в него формулу = ТРАНСП(А2:В4).

Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>, в ячейках выделенного диапазона будут помещены элементы транспонированной матрицы.

Вычислить произведение А^ТА, для чего выделить диапазон (А9:В10) и ввести в него формулу =МУМНОЖ(А6:С7;А2:В4).

Вычислить произведение А^ТВ, для чего выделить диапазон из двух ячеек (Е6:Е7) и ввести в него формулу =МУМНОЖ(А6:С7;D2:D4).

Выделить диапазон (D9:Е10), ввести в него формулу =МОБР(А9:В10) для вычисления обратной матрицы (А^ТА)^-1. Матрица существует, следовательно, исходная система определена.

Для вычисления итогового результата – решения системы уравнения выделить диапазон (В12:В13) и ввести в него формулу умножения матриц (А^ТА)^-1 х А^ТВ =МУМНОЖ(D9:Е10;Е6:Е7).

Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>, в ячейках диапазона В12:В13 будет получен результат решения системы (Рисунок 8).

Рисунок 8

 

Приведенную задачу можно решить без промежуточных вычислений, а введя сразу все выражение для вычисления в строку формул.

Формула, которая дает решение системы Х = (А^ТА)^-1 х (А^ТВ) содержит две группы (заключенные в скобки), которые должны быть перемножены с помощью функции МУМНОЖ (аргумент 1; аргумент 2). Аргумент 1 сам является вычисляемым выражением (А^ТА)^-1, аргумент 2 также вычисляется - (А^ТВ).

Решение:

1. Выделить диапазон, в котором будет вычисляться результат, и, используя мастер функций, ввести в него функцию МУМНОЖ, перевести курсор в поле Массив 2 диалогового окна Аргументы функции, после чего щелкнуть по кнопке f_x, расположенной в левой части строки формул, – окно Аргументы функции закроется, а в строке формул появится выражение =МУМНОЖ(;) (символ «;» разделяет аргументы функции).

2. Первый аргумент является обратной матрицей результата произведения матриц. Поставить курсор в поле первого аргумента и, используя список Функции, включить функцию МОБР и закрыть окно Аргументы функции, щелкнув по кнопке f_x в левой части строки формул. При этом курсор остается в строке формул в поле аргумента функции МОБР.

3. Аргумент функции МОБР в рассматриваемой задаче является произведением матриц. Используя список Функции включить функцию МУМНОЖ. Перевести курсор в поле Массив 2 диалогового окна Аргументы функции и указать адрес массива, содержащего элементы матрицы А. Затем перевести курсор в поле Массив 1 диалогового окна и, используя список Функции, включить функцию ТРАНСП и в качестве ее аргумента указать адрес массива, содержащего элементы матрицы А. Щелкнуть на кнопке f_x – окно Аргументы функции закроется.

4. В строке формул установить курсор в область второго аргумента первой функции МУМНОЖ, Используя список Функции, включить функцию МУМНОЖ. Поскольку второй аргумент не нужно вычислять, в первую очередь указать его: в поле Массив 2 ввести адрес диапазона, в котором содержатся элементы вектора В.

5. Поставить курсор в поле Массив 1 диалогового окна Аргументы функции, используя список Функции, включить функцию ТРАНСП и в поле Массив этой функции указать адрес диапазона, в котором содержатся значения элементов матрицы А.

6. Нажать комбинацию клавиш <Ctrl>+<Shift>+<Enter>, в ячейках выделенного диапазона будет результат решения системы (Рисунок 9).

Рисунок 9

 

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: