 |
Общие подходы к проверке и оценке выполнения заданий
|
|
|
|
С развернутым ответом
Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.
Если решение заданий 21–26 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание. Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом.
В критериях оценивания по каждому конкретному заданию второй части экзаменационной работы эти общие позиции конкретизируются и пополняются с учетом содержания задания. Критерии разработаны применительно к одному из возможных решений, а именно, к тому, которое описано в рекомендациях. При наличии в работах учащихся других решений критерии вырабатываются предметной комиссией с учетом описанного общего подхода. Решения учащихся могут содержать недочеты, не отраженные в критериях, но которые, тем не менее, позволяют оценить результат выполнения задания положительно (со снятием одного балла). В подобных случаях решение о том, как квалифицировать такой недочет, принимает предметная комиссия.
|
|
|
Примеры оценивания ответов по каждому типу заданий
С развернутым ответом с комментариями.
Задача 21 (демонстрационный вариант 2016 г).
Сократите дробь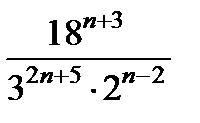 
.
Решение.
.
Ответ: 96.
Критерии оценки выполнения задания 21.
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Небольшое уточнение с «ошибка или описка» до «ошибки или описки» подчеркивает тот факт, что 1 балл допускается ставить в тех случаях, когда единственная вычислительная ошибка (описка) стала причиной того, что неверен ответ.
К вычислительным ошибкам не относятся ошибки в формулах при решении квадратного уравнения, действиях с числами с разными знаками, упрощении выражений со степенями и корнями и т.д.
Пример.
Решите уравнение 
.
Ответ: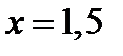 
, 
.
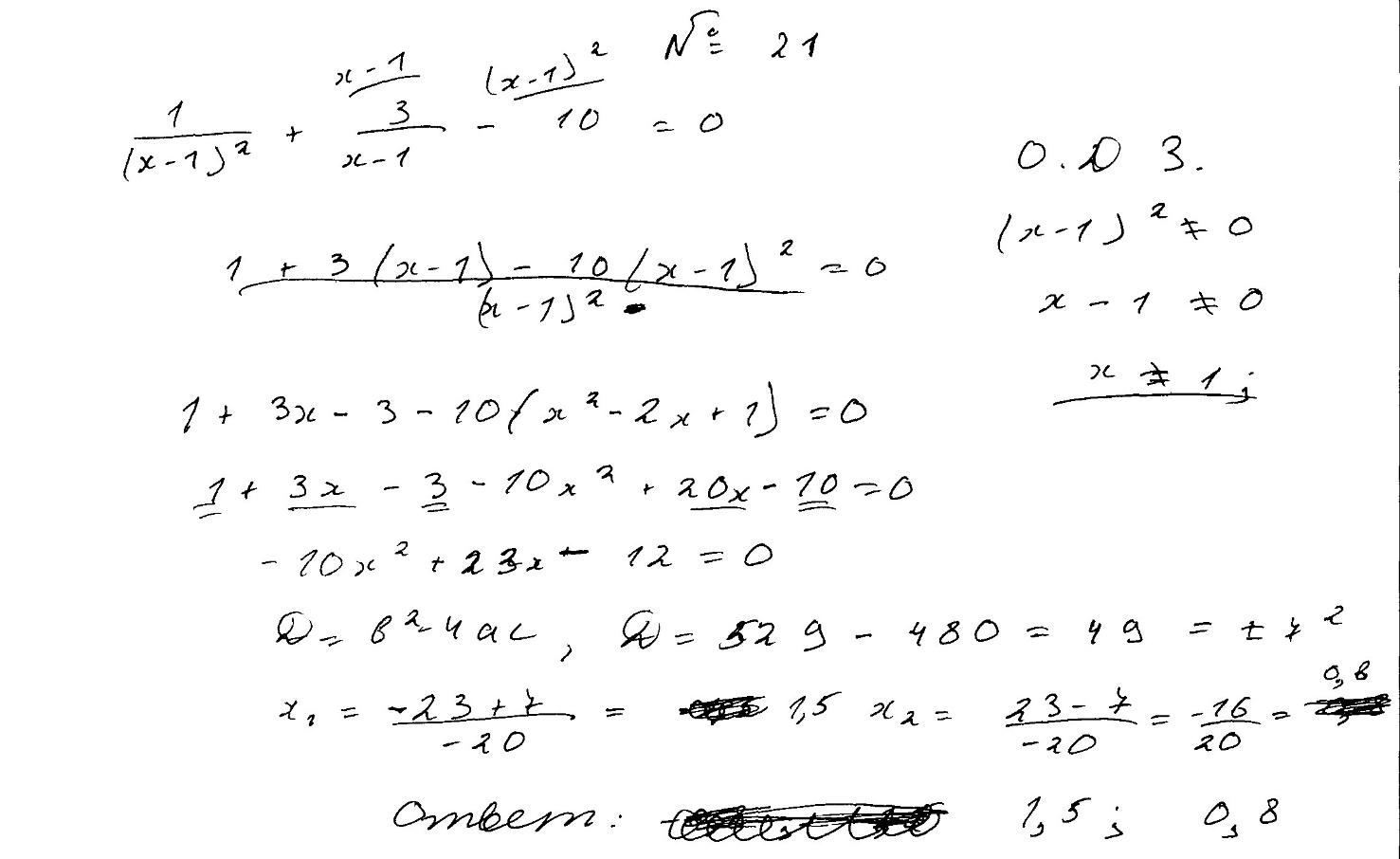
Комментарий.
Работа интересная – записан верный ответ. Но присутствуют в последних строках:
а) ошибка в вычислении корня квадратного уравнения;
б) ошибка при сложении чисел с разными знаками;
в) ошибка в формуле корней квадратного уравнения;
г) ошибка при делении чисел с разными знаками.
Оценка эксперта: 0 баллов.
Задача 22 (демонстрационный вариант 2016 г).
Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь. 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Решение.
|
|
|
Пусть искомое расстояние равно х км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно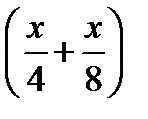 
часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение: 
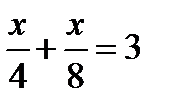. Решив уравнение, получим 
.
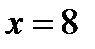Ответ: 8 км.
|
|
|
