 |
Пример оценивания решения задания 24.
|
|
|
|
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Комментарий.
Учащийся использует данные, которых нет в условии (считая острый угол ромба 60°).
Оценка эксперта: 0 баллов.
Задача 25 (демонстрационный вариант 2016 г).
В параллелограмме 
точка 
— середина стороны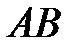 
. Известно, что 
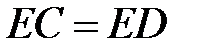. Докажите, что данный параллелограмм — прямоугольник.
Доказательство. Треугольник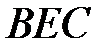и 
и 
равны по трём сторонам.
Значит, углы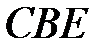 
и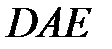 
равны. Так как их сумма равна 
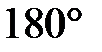, то углы равны 
. Такой параллелограмм — прямоугольник.
Критерии оценки выполнения задания 25.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Пример оценивания решения задания 25.
Пример.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий.
Не доказано, что точка F лежит на высоте EK.
Оценка эксперта: 0 баллов.
Задача 26 (демонстрационный вариант 2016 г).
Основание 
равнобедренного треугольника 
равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания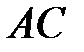 
. Найдите радиус окружности, вписанной в треугольник 
.
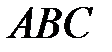Решение.
Пусть 
— центр данной окружности,
а 
— центр окружности, вписанной в треугольник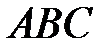 
.
Точка касания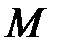 
окружностей делит 
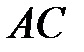пополам.
Лучи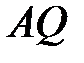 
и 
— биссектрисы смежных углов, значит, угол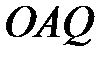 
прямой. Из прямоугольного треугольника 
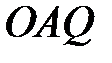получаем: 
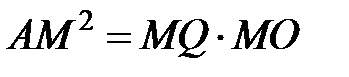. Следовательно,
|
|
|
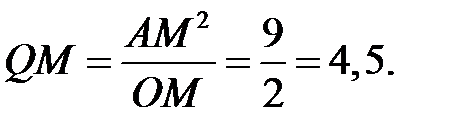
Ответ: 4,5.
Критерии оценки выполнения задания 26.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Пример оценивания решения задания 26.
Пример.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности.
Ответ: 5.
Комментарий.
При правильном ответе решение содержит более одной ошибки и описки.
Оценка эксперта: 0 баллов.
Материалы для практических занятий по оценке выполнения заданий
С развернутым ответом
Задание 21.
Пример 1.
Решите уравнение 
.
Ответ: 
, 
.
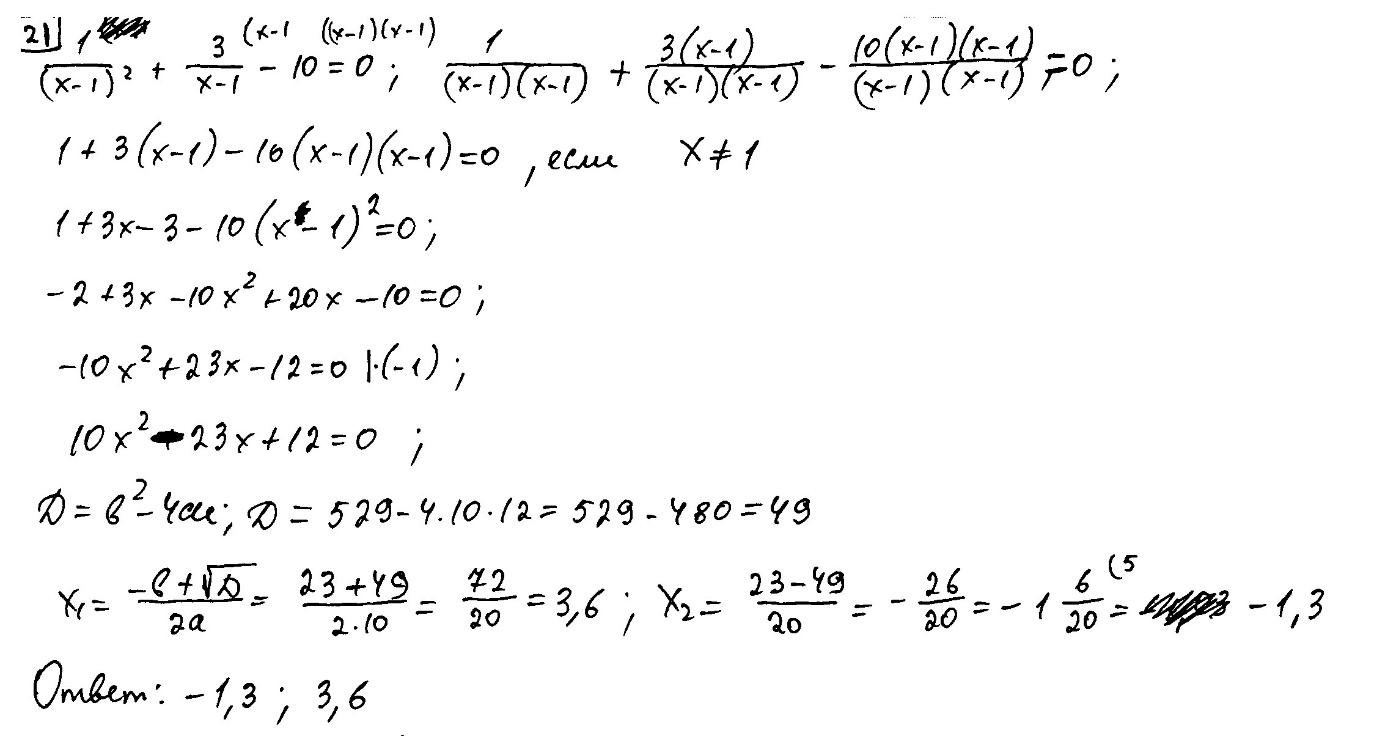
Комментарий.
При нахождении корней квадратного уравнения допущена неверная запись. При наличии общей формулы для нахождения корней квадратного уравнения, записанной верно, не извлечен корень из дискриминанта, все дальнейшие вычисления (с этой ошибкой) выполнены верно. Вычислительная ошибка присутствует, с её учётом дальнейшие шаги выполнены верно.
Оценка эксперта: 1 балл.
Пример 2.
Решите уравнение 
.
Ответ: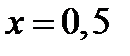 
, 
.
Комментарий.
Правильно выполнены преобразования, получен верный ответ.
Оценка эксперта: 2 балла.
Пример 3.
Решите уравнение .
Ответ: 
, .
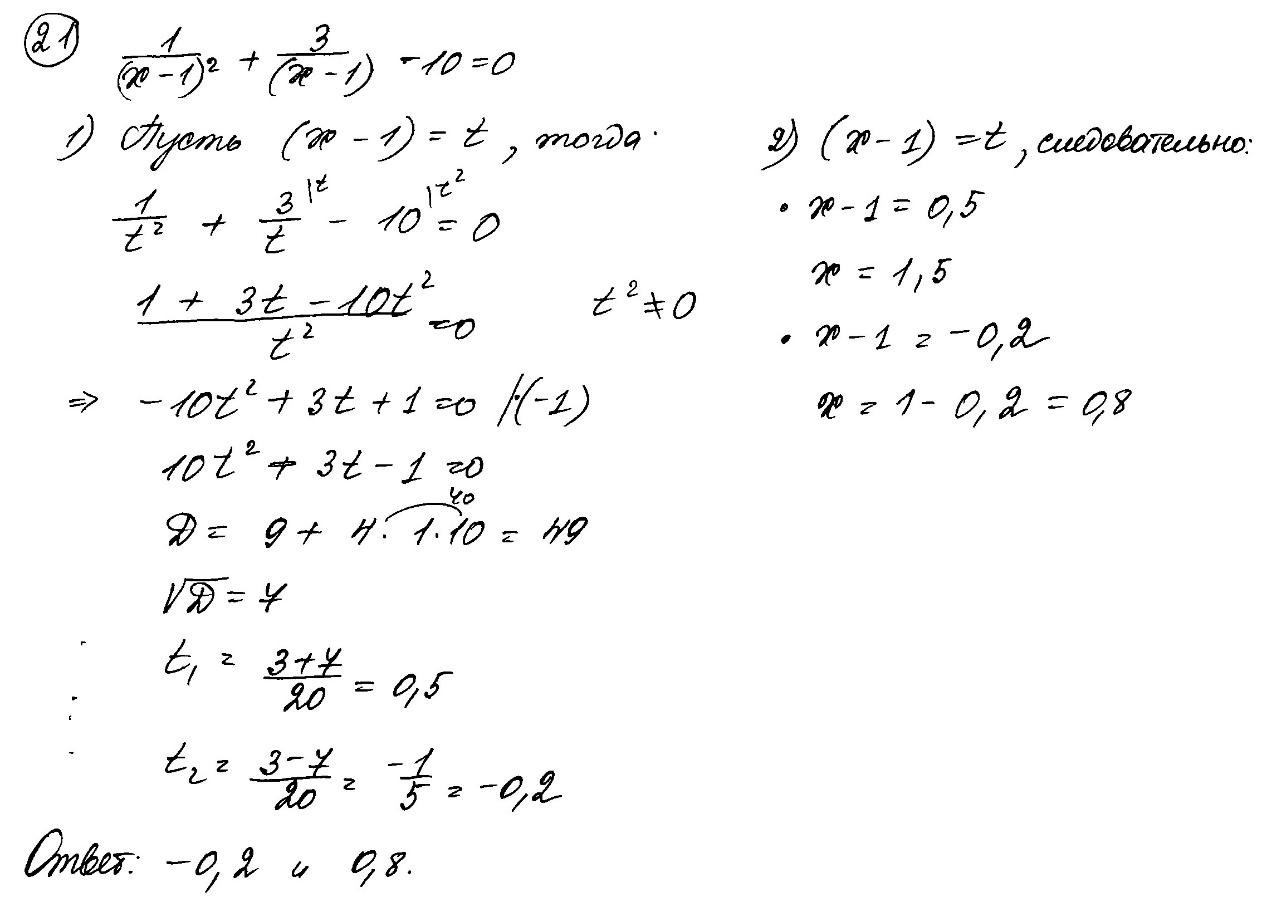
Комментарий.
Все этапы решения присутствуют, корни в правом столбце найдены верно. Неверную запись ответа можно рассмотреть как описку.
Оценка эксперта: 1 балл.
Пример 4.
Решите уравнение .
Ответ: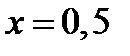 
, .
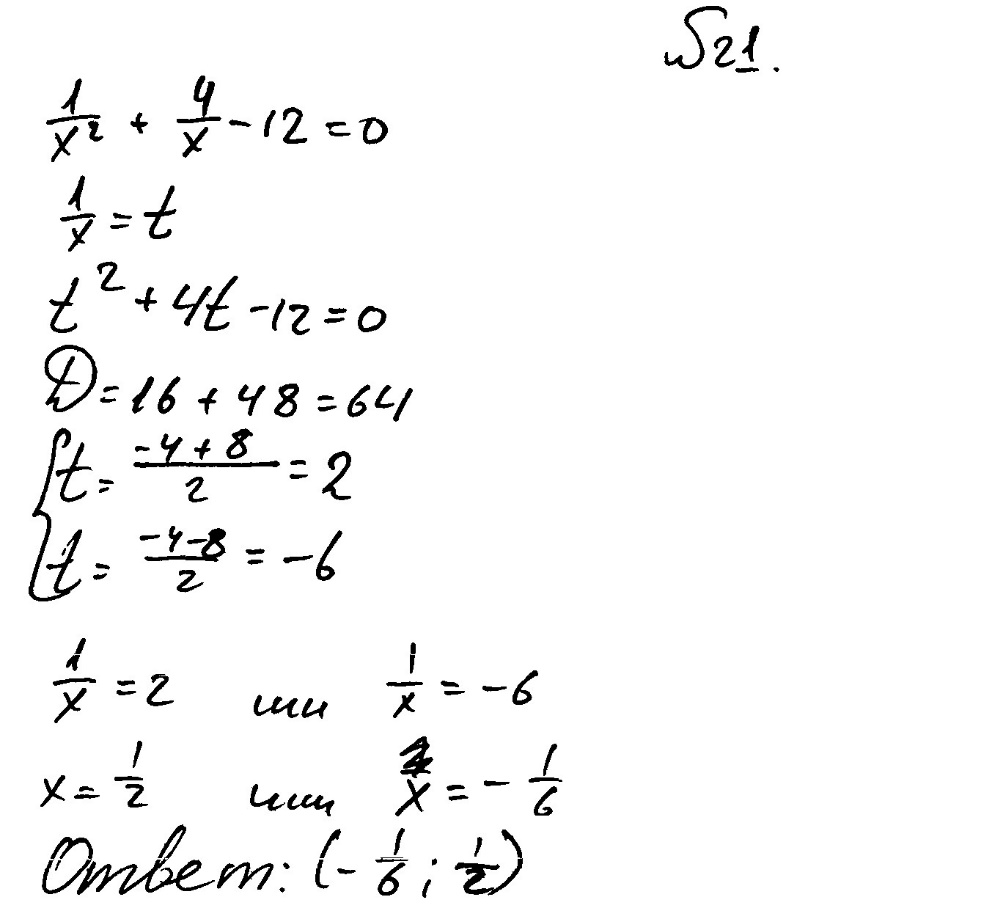
Комментарий.
Все этапы решения присутствуют, корни найдены верно. Неверную запись ответа можно рассмотреть как неверное владение символикой (хочется надеяться, что учащийся хотел написать фигурные скобки).
|
|
|
Оценка эксперта: 1 балл.
Задание 22.
Пример 1.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 900 минут.
Комментарий.
Ход решения верный, ответ верный.
Оценка эксперта: 2 балла.
Пример 2.
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут.
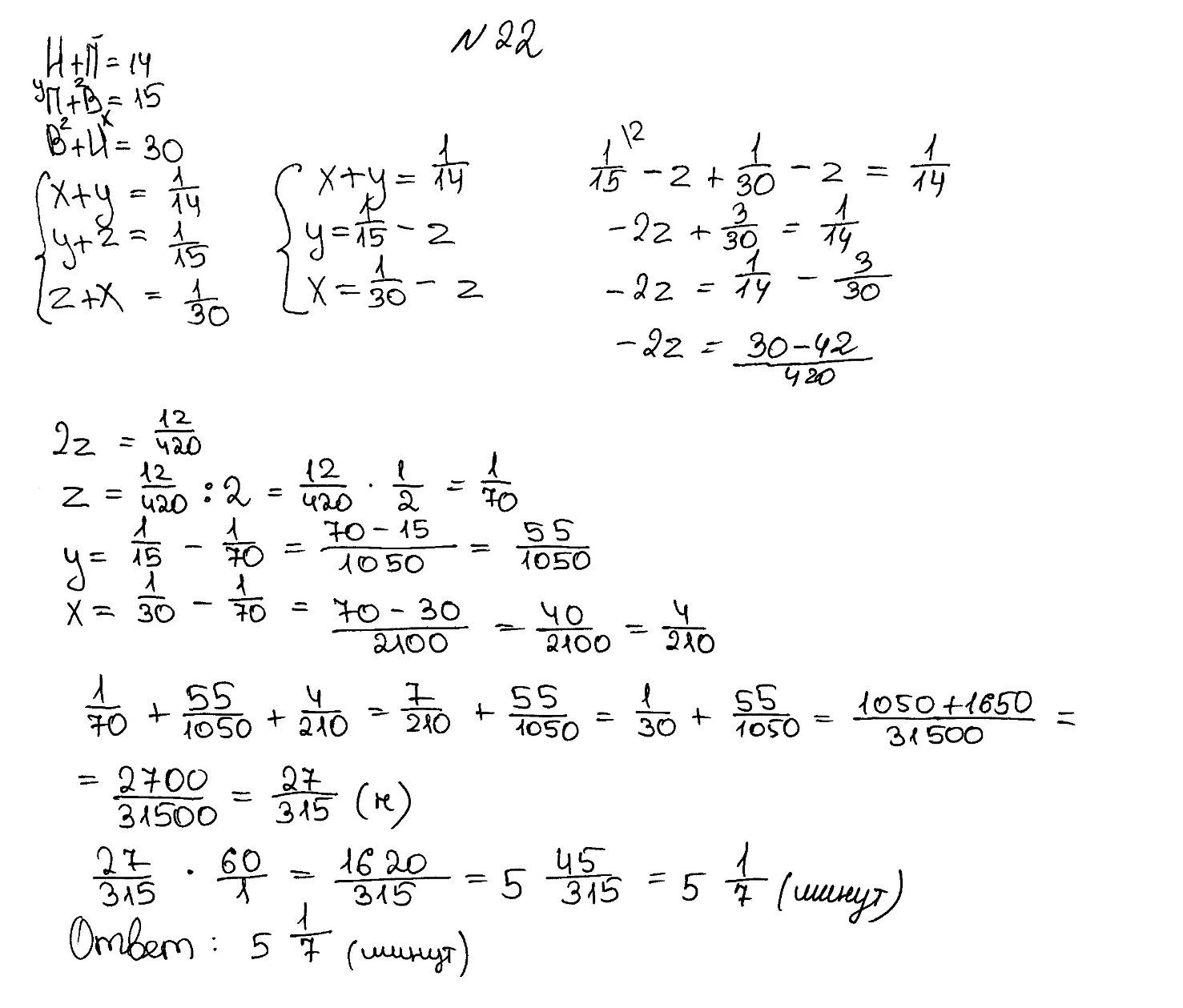
Комментарий.
Логическая ошибка – выпускник перепутал производительность и время.
|
|
|
