 |
Применение классической теории вероятностей
|
|
|
|
4.3.2.1 Задачи в условиях определенности
Пусть значения управляемых переменных  , критерий эффективности –
, критерий эффективности –  . Нужно выбрать их так, чтобы
. Нужно выбрать их так, чтобы  было максимальным (
было максимальным ( ). Пусть все факторы, определяющие нашу операцию, делятся на две группы:
). Пусть все факторы, определяющие нашу операцию, делятся на две группы:
 – управляемые и
– управляемые и
 – неуправляемые (внешние).
– неуправляемые (внешние).
Тогда задача исследования операции будет записана
 , где
, где  . (4.1)
. (4.1)
G – область определения, где нужно найти вектор решения. Решение задачи проводится при наложении на переменные ограничивающих условий. В зависимости от типа этих условий задачи делятся на линейные, нелинейные, выпуклые, динамические и т.д.
4.3.2.2 Задачи в условиях риска
Решение таких задач зависит от трех групп факторов:
1) управляемые факторы  ,
,
2) фиксированные неуправляемые факторы  ,
,
3) неизвестные (случайные) факторы с известным распределением  .
.
Тогда критерий эффективности запишется в виде:
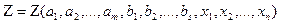 . (4.2)
. (4.2)
Пример – работа магазина, критерий: уменьшение времени обслуживания, чтобы не было очередей. Неизвестны моменты прихода покупателей и длительность обслуживания их продавцами, они являются случайными величинами, закон распределения которых можно найти, проведя специальные наблюдения и обработав их методами математической статистики.
Для решения задач в условиях риска используются два подхода:
1) cведение к задачам первого типа (в условиях определенности), путем замены значений  на их математические ожидания (интегралы) –
на их математические ожидания (интегралы) – 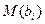 . Данный подход не всегда дает верный результат.
. Данный подход не всегда дает верный результат.
2) оптимизация в среднем – ищется максимум математического ожидания критерия  .
.
Применение оптимизации в среднем, сопровождается риском, так как в каждом отдельном случае могут быть большие расхождения между средними выбранными значениями критерия эффективности и значением эффективности в реальной ситуации. При многократном повторении этой операции различия сглаживаются. Таким образом, применяя этот прием, для часто случающихся ситуаций в среднем получают наибольший выигрыш. Для оценки величины риска используют дисперсию (среднеквадратичное отклонение  ).
).
|
|
|
Пример 1. Рассмотрим задачу для одного управляемого фактора  , принимающего значения
, принимающего значения  . Неуправляемый случайный фактор –
. Неуправляемый случайный фактор –  , с дискретными значениями
, с дискретными значениями  .
.
Определены условные вероятности  , известны
, известны  . Тогда математическое ожидание
. Тогда математическое ожидание  при значениях
при значениях 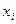 и
и  будет записано:
будет записано:
 , (4.3)
, (4.3)
и задача сводится к нахождению
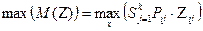 . (4.4)
. (4.4)
Пример 2. Пусть предприятие заказывает определенный тип деталей и цена одной детали -  , а отсутствие детали на складе при поломке обходится в
, а отсутствие детали на складе при поломке обходится в  .
.
Данные о частоте выхода из строя этой детали даны в таблице 4.1
Таблица 4.1
| Потребность в запасных деталях | ... | k | |||
| Число станков требующих детали | 
| 
| 
| ... | 
|
| Вероятность выхода из строя детали | 
| 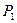
| 
| ... | 
|
Определить сколько нужно заказать деталей, чтобы затраты были минимальны.
Составим модель. Пусть  – число купленных деталей,
– число купленных деталей,  – потребность в деталях. Тогда запасу в
– потребность в деталях. Тогда запасу в  деталей будут соответствовать затраты
деталей будут соответствовать затраты
 . (4.5)
. (4.5)
Хотя нам не известно заранее, сколько деталей потребуется, но вероятность выхода из строя определенного числа деталей  известны (т.е. спрос на детали является случайной величиной).
известны (т.е. спрос на детали является случайной величиной).
Тогда ожидаемые затраты (математическое ожидание) как функция уровня запасов запишется виде
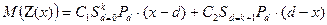 , (4.6)
, (4.6)
и задача сводится к нахождению величины  , для которой
, для которой 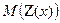 будет минимальна.
будет минимальна.
4.3.2.3. Задачи в условиях неопределенности
Принятие управленческих решений предполагает наличие ситуаций выбора наиболее выгодного варианта поведения из нескольких имеющихся вариантов в условиях неопределённости. Такие задачи рассматриваются в теории игр и могут быть описаны матричными играми особого типа, в которых игрок взаимодействует не со вторым игроком, а с окружающей средой. Объективно окружающая среда не заинтересована в проигрыше игрока. В процессе принятия решения о выборе варианта поведения игрок имеет информацию о том, что окружающая среда может принять одно из нескольких возможных состояний и сталкивается с неопределённостью относительно того конкретного состояния, которое примет окружающая среда в данный момент времени.
|
|
|
Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учётом неопределённости состояния окружающей среды, называется статистической игрой или «игрой с природой». Игрок в этой игре называется лицом, принимающим решение (ЛПР).
Матричная игра в теории игр описывается с помощью платежной матрицы. В общем виде платёжная матрица статистической игры приведена на рис. 4.2.

| 
| … | 
| |

| 
| 
| ... | 
|

| 
| 
| ... | 
|
| … | ... | ... | ... | ... |

| 
| 
| ... | 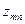
|
Рис. 4.2. Общий вид платёжной матрицы статистической игры
В данной игре строки матрицы (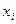 ) – стратегии ЛПР, а столбцы матрицы (
) – стратегии ЛПР, а столбцы матрицы ( ) – состояния окружающей среды, представляющие собой неопределенный фактор с неизвестным законом распределения вероятностей. Выбор решения основывается на принципе получения максимальной гарантированной величины показателя эффективности, отраженного значениями
) – состояния окружающей среды, представляющие собой неопределенный фактор с неизвестным законом распределения вероятностей. Выбор решения основывается на принципе получения максимальной гарантированной величины показателя эффективности, отраженного значениями  .
.
При фиксировании конкретного значения  мы получаем задачу первого типа. Решение задач в условиях неопределенности зависит от выбранного критерия оптимальности:
мы получаем задачу первого типа. Решение задач в условиях неопределенности зависит от выбранного критерия оптимальности:
 . (4.7)
. (4.7)
ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи. Результат решения задачи ЛПР определяет по одному из критериев оптимальности (критериев принятия решения). Для того чтобы прийти к однозначному и по возможности наиболее выгодному варианту решения, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (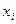 ) приписывается некоторый результат
) приписывается некоторый результат  , характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент
, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент  , который наилучшим образом отражает мотивацию его поведения.
, который наилучшим образом отражает мотивацию его поведения.
|
|
|
Критерий максимального математического ожидания выигрыша
Критерий максимального математического ожидания выигрыша применяется в тех случаях, когда ЛПР известны вероятности состояний окружающей среды. Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой значение математического ожидания выигрыша при выборе соответствующей стратегии ЛПР:
 , (4.8)
, (4.8)
где  – вероятность j-го состояния окружающей среды.
– вероятность j-го состояния окружающей среды.
Оптимальной по данному критерию считается такая стратегия ЛПР, при выборе которой значение математического ожидания выигрыша максимально:
 . (4.9)
. (4.9)
Применение критерия максимального математического ожидания выигрыша, таким образом, оправдано, если ситуация, в которой принимается решение, следующая:
1) ЛПР известны вероятности всех состояний окружающей среды,
2) минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.
Необходимость иметь информацию о вероятностях состояний окружающей среды ограничивает область применения данного критерия.
Критерий недостаточного основания Лапласа
Данный критерий используется при наличии неполной информации о вероятностях состояний окружающей среды в задаче принятия решения. Критерий Лапласа основан на принципе Бернулли: если нет оснований считать одно состояние более вероятным чем другие, то они считаются равновероятными. Т.о. вероятности состояний окружающей среды принимаются равными, и по каждой стратегии ЛПР в платёжной матрице определяется среднее значение выигрыша:
 , (4.10)
, (4.10)
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально:
 . (4.11)
. (4.11)
Использование данного критерия оправдано в следующих ситуациях:
1) ЛПР не имеет информации, либо имеет неполную информацию о вероятностях состояний окружающей среды,
2) вероятности состояний окружающей среды близки по своим значениям,
|
|
|
3) минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.
Максиминный критерий Вальда (критерий осторожного наблюдателя)
Правило выбора решения в соответствии с максиминным критерием (ММ-критерием) можно интерпретировать следующим образом. Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:
 . (4.12)
. (4.12)
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:
 . (4.13)
. (4.13)
Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных.
Применение ММ-критерия оправдано, если ситуация, в которой принимается решение следующая:
1) о возможности появления состояний окружающей среды ничего не известно,
2) решение реализуется только один раз,
3) необходимо исключить какой бы то ни было риск.
Критерий минимаксного риска Сэвиджа
Величина ( ), где
), где  – максимальный элемент j-го столбца, может быть интерпретирована как дополнительный выигрыш, получаемый в условиях состояния окружающей среды
– максимальный элемент j-го столбца, может быть интерпретирована как дополнительный выигрыш, получаемый в условиях состояния окружающей среды  при выборе ЛПР наиболее выгодной стратегии, по сравнению с выигрышем, получаемым ЛПР при выборе в тех же условиях любой другой стратегии. Эта же разность может быть интерпретирована как величина возможного проигрыша при выборе ЛПР i-ой стратегии по сравнению с наиболее выгодной стратегией. На основе данной интерпретации разности выигрышей производится определение наиболее выгодной стратегии по критерию минимаксного риска.
при выборе ЛПР наиболее выгодной стратегии, по сравнению с выигрышем, получаемым ЛПР при выборе в тех же условиях любой другой стратегии. Эта же разность может быть интерпретирована как величина возможного проигрыша при выборе ЛПР i-ой стратегии по сравнению с наиболее выгодной стратегией. На основе данной интерпретации разности выигрышей производится определение наиболее выгодной стратегии по критерию минимаксного риска.
Для определения оптимальной стратегии по данному критерию на основе платёжной матрицы рассчитывается матрица рисков, каждый коэффициент которой ( ) определяется по формуле:
) определяется по формуле:
 . (4.14)
. (4.14)
Матрица рисков дополняется столбцом, содержащим максимальные значения коэффициентов  по каждой из стратегий ЛПР:
по каждой из стратегий ЛПР:
 . (4.15)
. (4.15)
Оптимальной по данному критерию считается та стратегия, в которой значение  минимально:
минимально:
 . (4.16)
. (4.16)
Ситуация, в которой оправдано применение критерия Сэвиджа, аналогична ситуации ММ-критерия, однако наиболее существенным в данном случае является учёт степени воздействия фактора риска на величину выигрыша.
Критерий пессимизма-оптимизма Гурвица
В практике принятия решений ЛПР руководствуется не только критериями, связанными с крайним пессимизмом или учётом максимального риска. Стараясь занять наиболее уравновешенную позицию, ЛПР может ввести оценочный коэффициент, называемый коэффициентом пессимизма, который находится в интервале [0, 1] и отражает ситуацию, промежуточную между точкой зрения крайнего оптимизма и крайнего пессимизма. Данный коэффициент определяется на основе статистических исследований результатов принятия решений или личного опыта принятия решений в схожих ситуациях.
|
|
|
Платёжная матрица дополняется столбцом, коэффициенты которого рассчитываются по формуле:
 , (4.17)
, (4.17)
где С – коэффициент пессимизма. Оптимальной по данному критерию считается стратегия, в которой значение  максимально:
максимально:
 . (4.18)
. (4.18)
При  критерий Гурвица превращается в ММ-критерий. При
критерий Гурвица превращается в ММ-критерий. При  он превращается в критерий “азартного игрока”, делающего ставку на то, что «выпадет» наилучший случай.
он превращается в критерий “азартного игрока”, делающего ставку на то, что «выпадет» наилучший случай.
Критерий Гурвица применяется в ситуации, когда:
1) информация о состояниях окружающей среды отсутствует или недостоверна,
2) необходимо считаться с появлением каждого состояния окружающей среды,
3) реализуется только малое количество решений,
4) допускается определенный риск.
Критерий Ходжа-Лемана
Этот критерий опирается одновременно на ММ-критерий и критерий максимального математического ожидания выигрыша. При определении оптимальной стратегии по этому критерию вводится параметр достоверности информации о распределении вероятностей состояний окружающей среды, значение которого находится в интервале [0, 1]. Если степень достоверности велика, то доминирует критерий максимального математического ожидания выигрыша, в противном случае – ММ-критерий.
Платёжная матрица дополняется столбцом, коэффициенты которого определяются по формуле:
 , (4.19)
, (4.19)
где с – параметр достоверности информации о вероятностях состояний окружающей среды.
Оптимальной по данному критерию считается та стратегия, в которой значение  максимально:
максимально:
 . (4.20)
. (4.20)
Данный критерий применим в следующем случае:
1) имеется информация о вероятностях состояний окружающей среды, однако эта информация получена на основе относительно небольшого числа наблюдений и может измениться,
2) принятое решение теоретически допускает бесконечно много реализаций,
3) при малом числе реализации допускается некоторый риск.
Пример. Правительство собирается построить электростанцию и необходимо выбрать ее тип из 4 возможных:  – тепловые,
– тепловые,  – приплотинные,
– приплотинные,  – бесшлюзовые,
– бесшлюзовые, 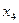 – шлюзовые. Эффективность работы ЭС зависит от внешней среды: режима рек, топлива.
– шлюзовые. Эффективность работы ЭС зависит от внешней среды: режима рек, топлива.
Допустим, что в состоянии среды выделено 3 разных состояния  ,
,  ,
,  . Экономическая эффективность станции зависит от состояния среды и определяется по таблице 4.3.
. Экономическая эффективность станции зависит от состояния среды и определяется по таблице 4.3.
Таблица 4.3
| Состояние среды / тип станции | 
| 
| 
| 
| 
|

| |||||

| |||||

| |||||
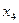
|
Решение.
1) по критерию Вальда  и следует строить станцию типа
и следует строить станцию типа  .
.
2) по критерию Сэвиджа матрица рисков будет выглядеть
Таблица 4.4
| x/y | 
| 
| 
| 
|

| -3 | -8 | -8 | |

| -6 | -4 | -6 | |

| -5 | -2 | -5 | |
| -7 | -6 | -4 | -7 |
Тогда  и строить нужно станцию типа
и строить нужно станцию типа  .
.
3) критерий Гурвица при  дает
дает  , и, следовательно, нужно строить станцию типа
, и, следовательно, нужно строить станцию типа  .
.
4) критерий Лапласа при  имеет максимальное значение при строительстве станции типа
имеет максимальное значение при строительстве станции типа  .
.
Таким образом, решение зависит от выбранного критерия.
|
|
|


