Методы принятия решения

На практике индивидуальные задачи принятия решений весьма распространены в обществе. Широкая распространенность задач индивидуального выбора, возможность учесть коллективные предпочтения, пристра­стия и интересы активных групп при решении этих задач делают в настоящее время проблемы индивидуального выбора наиболее практически важным классом задач принятия решений.

 

Альтернативы

Варианты действий принято называть альтернативами. Альтернативы – неотъемлемая часть проблемы принятия решений: если не из чего выбирать, то нет и выбора. Следовательно, для постановки задачи принятия решений необходимо иметь хотя бы две альтернативы.

Альтернативы бывают независимыми и зависимыми. Неза­висимыми являются те альтернативы, любые действия с кото­рыми (удаление из рассмотрения, выделение в качестве единст­венно лучшей) не влияют на качество других альтернатив. При зависимых альтернативах оценки одних из них оказывают влияние на качество других. Имеются различные типы зависи­мости альтернатив. Наиболее простым и очевидным является непосредственная групповая зависимость: если решено рассмат­ривать хотя бы одну альтернативу из группы, то надо рассмат­ривать и всю группу.

Задача принятия решений

< Т, А, К, X, F, G, D >,

где Т - постановка задачи;

А - множество альтернатив;

К - множество критериев;

Х - множество шкал оценок критериев;

F - отображение множества допустимых решений в множество предпоч­тений эксперта;

D - решающее правило, называется многокритериальной, если множество К содержит два или более элементов.

Необходимо отметить, что большинство реальных задач принятия ре­шений являются многокритериальными. В частности, при проектировании ин­формационных комплексов системные интеграторы анализируют различные ва­рианты их архитектурного построения на основе значений таких критериев, как: реактивность, стоимость, надежность. Очевидно, что конструктор стремится вы­брать вариант, обеспечивающий высокую реактивность, низкую стоимость и по­вышенную надежность. Однако достигнуть наилучших значений одновременно по перечисленным критериям невозможно.

Задачи принятия решений существенно различаются также в зависимости от наличия альтернатив на момент выработки политики и принятия решений. Встречаются задачи, когда все альтернативы уже заданы, уже определены, и необходимо лишь выбрать лучшие из этого множества. Особенностью этих задач является замкнутое, не расширяющееся множество альтернатив. Но существует множество задач другого типа, где все альтернативы или их значительная часть появляются после принятия основных решений.

Когда альтернатив много (сотни и тысячи), внимание ЛПР (человек или группа людей) не может сосредоточиться на каждой из них. В таких ситуаци­ях возрастает необходимость в четких правилах выбора, в про­цедурах использования экспертов, в разработке совокупности правил, позволяющих проводить в жизнь непротиворечивую и последовательную политику.

Во всем этом существует потребность и тогда, когда число альтернатив невелико (до 20), но они не являются единственно возможными. Часто на их ос­нове в процессе выбора возникают новые альтернативы. Пер­вичные, основные альтернативы не всегда удовлетворяют уча­стников процесса выбора. Однако они помогают им понять, чего конкретно не хватает, что реализуемо при данной ситуации, а что нет. Этот класс задач можно назвать задачами с конструи­руемыми альтернативами.

Принятие решения на основе выбора одной из альтернатив из получен­ного при техническом прогнозировании (моделировании) множества воз­можных исходов является уделом ЛПР (лиц, принимающих решения). На характер принятия решения оказывают влияние внешние и внутренние причины:

- к внешним относятся: время на принятие решений, структура ор­ганизации (уровень оснащенности вычислительной техникой, наличие аналитического отдела), цели стоящие перед ЛПР;

- к внутренним - стиль принятия решений: интуитивный и аналити­ческий. Причем взгляд, что корректный математический подход предпо­чтительней не бесспорен. Зачастую эвристический подход, относящийся к творческой деятельности естественного и искусственного интеллектов, может привести к более эффективным решениям, хотя эта проблема требует еще и четкой постановки и путей решения. Считая, что, пользуясь аналити­ческими методами можно четко описать альтернативу, возможную стра­тегию ее осуществления и даже последствия применения этой стратегии, необходимо провести оценку альтернатив с учетом их субъективной по­лезности или КЦФ. К неправильным решениям может привести:

- ложные исходные предпосылки;

- неправильное толкование исходных данных и ошибочный прогноз;

- неверное или злонамеренное поведение ЛПР.

Однократное решение не позволяет делать далеко идущие выводы и поэтому необходимо создавать механизм целенаправленной деятельности по принятию решений, что возможно только при условии использования ИТ. В этом процессе должны участвовать, поддержанные ВТ: а) ЛПР, несу­щие всю ответственность за принимаемое решение, б) эксперты и/или экс­пертная система и лица, обеспечивающие принятие решения - ЛОР не несущие непосредственной ответственности за принятие решения.

Относительно любой пары сравниваемых альтернатив можно вво­дить отношения эквивалентности либо предпочтения. Из конечного и счетно­го множества исходов прогнозирования необходимо выбрать ограниченное число, а в идеале одно решение. При этом:

1. Сравнение можно проводить по одному или нескольким критериям, которые могут оцениваться количественными значениями (парамет­ры) или качественными (альтернативными типа больше - меньше, хуже - лучше).

2. Принятие решения чаще всего проводится в условиях неопреде­ленности и стохастичности.

3. Принятие решений зависит от интересов сторон (кооперативный
выбор, выбор в конфликтной ситуации, компромисс и т.д.)

Альтернатива А называется доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем оценка альтернативы В, а хотя бы по одному критерию оценка альтернативы А лучше, чем оценка альтернативы В, Альтернатива В определяется как доминируемая. Альтернативы являются эффективными, или, иначе принадлежащими множеству Эджворта-Парето, если каждая из них превосходит любую другую по какому-либо из критериев. Эффективные альтернативы не сравнимы между собой на основе критериальных оценок, и лучшая из них может быть вы­брана только с учетом дополнительной информации, отражающей предпочтения лица, принимающего решения.

Таким образом, предварительный этап решения многокритериальных задач состоит в попарном сравнении альтернатив и исключении доминируемых. Дальнейший поиск оптимального варианта определяется типом анализируемой проблемы. Для структурированных проблем, описываемых объективными моде­лями, представляется возможным количественное определение значений критериальных оценок для различных параметров и ограничений. Это свойство позво­ляет использовать такие методы, как: аддитивной либо мультипликативной свер­ток; выбора главного критерия и перевод остальных критериев в ограничения; уступок; поиска удовлетворительных значений критериев (STEM).

Естественно, что аналитическое описание в каждом случае будет различным, поэтому остановимся на общей идее формальной структуры принятия решения. Предположим, что каждая альтернатива E_i, получен­ная в результате прогнозирования, E_iÎЕ. Е - конечное множество альтерна­тив, 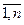. Каждый вариант E_i однозначно определяется результатом e_i, который должен допускать количественную или качественную (квалиметрическую) оценку.

Естественно, что искомый вариант должен иметь максимальное значе­ние e_i. Критерий в этом случае должен иметь вид:

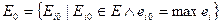, (4.21)

что читается: «множество E₀ оптимальных вариантов, состоит из тех вариантов E_i0, которые принадлежат мно­жеству Е и оценка которых макси­мальна среди всех оценок e_i». Выбор оптимального варианта в соответствии с (1) не является однозначным и приводит к Паретовскому множеству. (Под компромиссным или множеством по Парето понимается множество, состоящее из максимальных значений частных критериев различных альтернатив. Это происходит, когда предпочтение по одному критерию расходится с предпочтением по другому и альтернативы становятся не доминируемыми, т.е. не сравнимыми.) На рисунке 4.4 показана разница между различными критериями в случае пространства двух параметров.

 

Рис. 4.4. Иллюстрация методов принятия решений:

а – суперкритерий; б – метод уступок; в – метод Парето.

 

Рассмотрим вначале случай, когда варианту решения Е, вследствие различных внешних условий F_j соответствуют различные результаты е_ij, создавая матрицу решений | е_ij |.

Таблица 4.5

	F1	…	Fj	…	Fm
E1	e11	…	e1i	…	e1m
:	:		:		:
Ei	ei1	…	eij	…	eij
:	:		:		:
En	en1	…	enj	…	enm

 

Поэтому начальная задача максимизации e_i согласно (4.21) должна быть заменена другой учитывающей последствия любого варианта. Для этого необходимо ввести оценочные функции. При этом матрица решений сводится к одному столбцу и каждому варианту Е_i приписывается некоторый результат e_ir, характеризующий все последствия этого решения. Тогда каждое из альтер­нативных решений будет характеризоваться комбинацией из наибольшего и наименьшего результатов:

e_ir = min e_ij + max e_ij. (4.22)

На основе (4.22) получается способ построения оценочных функций:

max e_ir = max (min e_ij + max e_ij). (4.23)

При оптимистической позиции (азартный игрок) ищется наилучшее решение:

max e_ir =max (max e_ij). (4.24)

В нейтральной позиции максимум среди математических ожиданий:

max e_ir = max (1/m 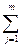e_ij). (4.25)

В пессимистической позиции максимум среди минимальных решений:

max e_ir = max (min e_ij). (4.26)

 

Оценка (4.24) обычно на практике не используется. Влияние ЛПР на эффективность решения иллюстрируется на рис. 4.5.

Рис. 4.5. Поле полезности решения:

УТ – утопическая точка; РТ – рассматриваемая точка;

АУТ – антиутопическая точка.

 

Под утопической точкой пони­мается оптимистическое решение, рассматриваемые точки лежат внутри прямоугольника, называемого полем полезности решения. При сравнении вариантов Е_k будет не хуже Е₁, если е_k1 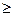e_l1, a е_k2 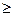e_l2,или лучшим если неравенства строгие, в случае когда е_k1>e_l1, а е_k1<e_l1,то установ­лен только частичный порядок. Введя в центре прямоугольника точку РТ, плоскость разбивается на четыре области (при произвольной размерности получаются конусы). Тогда все точки области (конуса) 1 лучше РТ и получаем область предпочтения, область 3 хуже РТ (антиконус), области же 2 и 4 - области неопределенности, оценка в которых производится только с помощью критериев принятия решения.

В случае п решений и т состояний критерий имеет вид:

max K (e_{i 1},…, e_{i m}), i = ,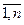

min K (e_{i 1},…, e_{i m}), i = ­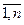. (4.27)

Функция т переменных К характеризует критерий и задает оценочную функцию, полагая e_i1=х₁ и так далее, рассмотрим функцию К на всем n -мерном пространстве R^m, тогда значению параметра К = К(х₁,..., х_т) ставится в соответствие гиперпо­верхность, называемая поверхностью уровня. В рассматриваемом двумерном случае, положив e_i1=x₁=и, e_i2=x₂=v,с помощью равенства K(u,v) = К полу­чаем на плоскости кривую, называемую линией уровня, которая соответствует значению К. При фиксированном уровне К получаем функциональную зависимость - функцию предпочтения, представленную на рис. 4.6.

 

Рис. 4.6 Функция предпочтения

 

Для выражения (4.24) функция представляется биссектрисой 2 и 4 областей, все точки справа и выше лучше точек слева и ниже. Естественно, что всё сказанное является лишь иллюстрацией общего подхода.

Критерии

В современной науке о принятии решений считается, что варианты решений характеризуются различными показателями их привлекательности для ЛПР. Эти показатели называют признаками, факторами, атрибутами или критериями. Мы принимаем для последующего изложения термин «критерий».

Будем называть критериями оценки альтернатив показатели их привлекательности (или непривлекательности) для уча­стников процесса выбора.

В профессиональной деятельности выбор критериев часто определяется многолетней практикой, опытом. В подавляющем большинстве задач выбора имеется достаточно много критериев оценок вариантов решений. Эти критерии могут быть незави­симыми или зависимыми. Зависимыми называются те крите­рии, при которых оценка альтернативы по одному из них опре­деляет (однозначно либо с большой степенью вероятности) оцен­ку по другому критерию. Зависимость между критериями приводит к появлению целост­ных образов альтернатив, которые имеют для каждого из участ­ников процесса выбора определенное смысловое содержание.

На сложность задач принятия решений влияет также коли­чество критериев. При небольшом числе критериев (два – три) за­дача сравнения двух альтернатив достаточно проста и прозрачна, качества по критериям могут быть непосредственно сопоставлены и выработан компромисс. При большом числе критериев задача становится малообозримой. К счастью, при большом количестве критериев они обычно могут быть объединены в группы, имею­щие конкретное смысловое значение и название. Основанием для естественной группировки критериев является возможность вы­делить плюсы и минусы альтернатив, их достоинства и недостат­ки (например, стоимость и эффективность). Такие группы, как правило, независимы. Выявление структуры на множестве кри­териев делает процесс принятия решений значительно более ос­мысленным и эффективным.

Появление многокритериальности

При широком применении методов исследования операций аналитики стали сталкиваться с задачами, где имеется не один, а несколько критериев оценки качества решения.

Различные задачи имеют следующую ха­рактерную особенность: модель, описывающая множество до­пустимых решений, объективна, но качество решения оценива­ется по многим критериям. Для выбора наилучшего варианта решения необходим компромисс между оценками по различным критериям. В условиях задачи отсутствует информация, позво­ляющая найти такой компромисс. Следовательно, он не может быть определен на основе объективных расчетов.

Анализ многих реальных практических проблем, с которы­ми сталкивались специалисты по исследованию операций, есте­ственным образом привел к появлению класса многокритери­альных задач. При появлении многих критериев задачи выбора наилуч­шего решения имеют следующие особенности.

Задача имеет уникальный, новый характер – нет статистических данных, позволяющих обосновать соотношения ме­жду различными критериями.

На момент принятия решения принципиально отсутствует информация, позволяющая объективно оценить возможные последствия выбора того или иного варианта решения. Но поскольку решение так или иначе должно быть принято, то недостаток информации необходимо восполнить. Это может быть сделано лишь людьми на основе их опыта и интуиции.

Первые многокритериальные решения

Одним из первых подходов к принятию решений при двух критериях является метод «стоимость–эффективность». Он был разработан в конце 50-х годов в США для решения военных задач. В годы ракетно-ядерной гонки США — СССР одной из основных была задача о достаточности системы нападения для преодоления защиты потенциального противника. Метод «стоимость—эффективность» состоит из трех основных этапов:

1) построения модели эффективности;

2) построения модели стоимости;

3) синтеза оценок стоимости и эффективности.

В общем случае на этапе синтеза стоимости и эффективности рекомендуется использовать два основных подхода: 1) фиксированной эффективности при минимально возможной стоимости (при таком подходе выбирается «самая дешевая» альтернатива, обладающая заданной эффективностью); 2) фиксированной стоимости и максимально возможной эффективности (случай бюджетных ограничений). Смысл этих подходов ясен – пе­ревод одного из критериев оценки альтернатив в ограничение.

Но при этом сразу же возникает вопрос: как, на каком уров­не установить ограничение на один из критериев. Объективный и единственно возможный ответ на этот вопрос в общем случае не вытекает из условий задачи. Ни требуемая эффективность, ни бюджетные ограничения не устанавливаются обычно достаточно жестко. Очевидно, что при нескольких критериях этот же вопрос становится существенно сложнее.

В ряде случаев используют отношение двух указанных вы­ше критериев. Авторы метода предостерегают против механиче­ского использования отношения стоимости к эффективности, указывая, что оно может быть одним и тем же при разных аб­солютных значениях числителя и знаменателя.

Третий подход к синтезу стоимости и эффективности при­водит к построению множества Эджворта-Парето (рис. 4.7). Сравним два варианта на множестве Эджворта-Парето. Вари­ант А менее дорогой, чем вариант В, но и менее эффективный. Вариант В более эффективный, чем вариант А, но и более доро­гой. Сравнивая варианты, находящиеся на множестве Парето, ЛПР останавливается на одном из них и делает свой оконча­тельный выбор.

 

Рис. 4.7. Множество Эджворта-Парето при двух критериях

Разные типы проблем

Подходы исследования операций и принятия решений существенно различаются, так как они направлены на принципиаль­но разные проблемы принятия решений, существующие в окружающем нас реальном мире. В известной классификации, пред­ложенной в 1958 г. в статье Г. Саймона и А. Ньюэлла, выде­ляются так называемые хорошо и слабоструктуризованные проблемы. Хорошо структуризованные, или количественно сфор­мулированные проблемы - те, в которых существенные зависи­мости выяснены настолько хорошо, что могут быть выражены в числах или символах, получающих в конце концов численные оценки. Слабоструктуризованные, или смешанные проблемы — те, которые содержат как качественные, так и количественные элементы, причем качественные, малоизвестные и неопределен­ные стороны проблем имеют тенденцию доминировать.

Важно подчеркнуть, что в типичных задачах исследования операций объективно существует реальность, допускающая строгое количественное описание и определяющая существова­ние единственного очевидного критерия качества. Изучение ре­альной ситуации может требовать большого труда и времени. Необходимая информация может быть дорогостоящей (напри­мер, требуются специальные исследования, чтобы определить значения ряда параметров). Однако при наличии средств и хо­рошей квалификации аналитиков имеются все возможности найти адекватное количественное описание проблемы, количе­ственные связи между переменными и критерий качества.

Можно сказать, что типичные проблемы исследования опе­раций являются хорошо структуризованными.

По-иному обстоит дело в многокритериальных задачах. Здесь часть информации, необходимой для полного и однознач­ного определения требований к решению, принципиально от­сутствует. Исследователь часто может определить основные пе­ременные, установить связи между ними, т. е. построить мо­дель, адекватно отражающую ситуацию. Но зависимости между критериями вообще не могут быть определены на основе объек­тивной информации, имеющейся в распоряжении исследовате­ля. Такие проблемы являются слабоструктуризованными, так как здесь недостаток объективной информации принципиально неустраним на момент принятия решения.

Более того, существуют проблемы, в которых известен только перечень основных параметров, но количественные свя­зи между ними установить нельзя (нет необходимой информа­ции). Иногда ясно лишь, что изменение параметра в определен­ных пределах сказывается на решении. В таких случаях струк­тура, понимаемая как совокупность связей между параметрами, не определена, и проблема называется неструктуризованной. Типичными неструктуризованными проблемами являются мно­гие проблемы выбора. Слабоструктуризованные и неструктуризованные проблемы исследуются в рамках научного направления, называемого принятием решений при многих критериях.

 

Оценки по критериям

Cуществуют шкалы оценок по критериям. В принятии решений принято различать шкалы непрерыв­ных и дискретных оценок, шкалы количественных и качест­венных оценок.

1. Шкала порядка - оценки упорядочены по возрастанию или убыванию качества. Примером может служить шкала эко­логической чистоты района около места жительства:

• очень чистый район;

• вполне удовлетворительный по чистоте;

• экологическое загрязнение велико.

2. Шкала равных интервалов – интервальная шкала. Для этой шкалы имеются равные расстояния по изменению качест­ва между оценками. Например, шкала дополнительной прибы­ли для предпринимателя может быть следующей: 1 млн, 2 млн, 3 млн и т.д. Для интервальной шкалы характерно, что начало отсчета выбирается произвольно, так же как и шаг (расстояние между оценками) шкалы.

3. Шкала пропорциональных оценок - идеальная шкала. Примером является шкала оценок по критерию стоимости, от­счет в которой начинается с установленного значения (напри­мер, с нулевой стоимости).

В принятии решений чаще всего используются порядковые шкалы и шкалы пропорциональных оценок.

Постановка многокритериальной задачи линейного программирования

Можно сформулировать многокритериальную задачу линейного программирования следующим образом.

Дано: область D допустимых значений переменных, опреде­ляемая совокупностью линейных равенств и неравенств; крите­рии Q, оценивающие качество решения.

Каждый из критериев линейно связан с переменными:

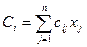. (4.28)

где n — число переменных (j =l,...,n); с_ij — числовые коэффици­енты.

Требуется: найти решение X в области D, при котором дос­тигаются наиболее приемлемые значения по всем критериям. Иначе говоря, нужно найти такие критериальные оценки, при которых достигается максимальное значение априори неизвест­ной функции полезности ЛПР.

Эта задача решается с помощью человеко-машинных про­цедур.

Весовые коэффициенты важности критериев

При появлении многокритериальных задач возникли до­полнительные трудности их решения, связанные с получением информации от ЛПР. Естественной реакцией на это было стремление получить такую информацию сразу и быстро устра­нить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так называе­мых весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле

, (4.29)

где С_i – частные критерии (i=l,..., N); w i – веса (коэффициенты важности) критериев:

. (4.30

Идея такого объединения состоит в том, что ЛПР назначает числа (часто по численной шкале 1-100), представляющие для него ценность рассматриваемого критерия. Считается, что ЛПР может назначить такие числа. Далее, весовые коэффициенты нормируются на основе условия (4.30).

Существует лемма, утверждающая, что для линейной задачи любое эффективное, находящееся на множестве Э-П решение может быть представлено в виде (4.29), т. е. в виде весов, умноженных на частные критерии. Следовательно, формально задача сводится к нахождению весов.

Возникла идея, что эти веса можно получить от ЛПР опера­тивно. Если ЛПР затрудняется в начале процесса решения (до изучения области D) сразу назвать эти веса, то можно построить ЧМП следующего содержания: ЛПР назначает первона­чальные веса, смотрит на решение и корректирует веса до по­лучения удовлетворительного результата.

Различные группы задач принятия решений

Представим в самых общих чертах группы задач принятия решений.

Задачи первой группы

Дано: группа из n альтернатив-вариантов решения пробле­мы и N критериев, предназначенных для оценки альтернатив; каждая из альтернатив имеет оценку по каждому из критериев.

Требуется: построить решающие правила на основе пред­почтений ЛПР, позволяющие:

а) выделить лучшую альтернативу;

б) упорядочить альтернативы по качеству;

в) отнести альтернативы к упорядоченным по качеству классам решений.

Задачи второй группы

Дано: группа из N критериев, предназначенных для оценки любых возможных альтернатив; альтернативы либо заданы частично, либо появляются после построения решающего пра­вила.

Требуется: на основании предпочтений ЛПР построить ре­шающие правила, позволяющие:

а) упорядочить по качеству все возможные альтернативы;

б) отнести все возможные альтернативы к одному из не­ скольких (указанных ЛПР) классов решений.

Примером задач первой группы является многокритериаль­ная оценка имеющихся в продаже товаров, например телевизо­ров или стиральных машин. Здесь все возможные альтернативы заданы, критерии определены ЛПР; оценки реальных альтернатив по критериям дают, как правило, эксперты. От ЛПР требует­ся построить правило сравнения объектов, имеющих оценки по многим критериям (например, сравнить стиральные машины на основании таких оценок, как цена, долговечность, стоимость эксплуатации, надежность, возможность ремонта и т. д.).

Примером задач второй группы является построение прави­ла принятия решений для государственного или частного фон­да, распределяющего ресурсы на научные исследования. Проек­ты проведения исследований еще не поступили, но критерии оценки и решающее правило должны быть определены заранее. Обычно таких проектов много, и можно предположить, что они будут достаточно разнообразны по оценкам. Критерии и ре­шающее правило определяют ЛПР. Затем уже поступают про­екты, которые оцениваются экспертами по заданным критери­ям. Решающее правило позволяет сразу же получить целостную оценку проекта.

Представленные выше две группы задач становятся весьма близки при рассмотрении в рамках первой задачи большого числа достаточно разнообразных (по своим оценкам) альтерна­тив. Но при малом числе заданных альтернатив методы реше­ния задач первой и второй групп существенно различаются.

 

Критерии принятия решения

1. Классический минимаксный критерий введён в 1950 году Вальдом и соответствует позиции крайней осторожности:

Z_MM = max e_ir, e_ir = min e_ij, (4.31)

E₀ = { E_i0|E_i0 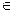Е e_i0 = max min e_ij }. (4.32)

Для этого критерия матрица решений дополняется ещё одним столб­цом из наименьших значений e_ir каждой строки. Выбирать надо те варианты E_i0, где стоят наибольшие значения e_ir этого столбца. Такой выбор полнос­тью исключает риск, и он применим, когда:

- ничего не известно о возможности изменения внешних факторов,
решение реализуется однократно;

- необходимо полностью исключить результаты хуже Z_MM.

2. Критерий Байеса-Лапласа учитывает каждое из возможных состоя­ний:

Z_MM = max e_ir, e_ir = , (4.33)

т.е. вводится строка математических ожиданий. Этот критерий расширяет гра­ницы минимаксного критерия, так как:

- известны вероятности появления или изменения внешних факторов;

- выбор может осуществляться многократно;

- появляется риск.

Существует ещё много других критериев: - вводящих понятие вы­игрыша (Сэвиджа), - уравновешивающих оптимизм и пессимизм (Гурвица), - объединяющих ММ и BL критерии (Ходжа-Леймана) и т.д. Очевидно, что все критерии используют минимаксный принцип, учиты­вая разные компоненты вероятности, весовых функций, критерий p, взя­тый из теории нечетких множеств Задэ. На практике применяют поочерёдно различные критерии, а затем принимают окончательное решение. Влияние критерия на вид оценочной функции проиллюстрируем на простейшем при­мере рассмотрения двух состояний F₁, F₂, когда у Î Е, а e_ir = f(e_i1, e_i2),то после подстановки имеем: и = е (у, F); v = e (y, F). С помощью f (u, v) = К задаётся семейство линий уровня, получаемых параллельным переносом на плоскос­ти (u, v) вдоль прямой, носящей название направляющей. Для минимаксного критерия ММ семейство конусов предпочтения лежит на линии х = у. В нашем случае необходимо перемещаться по биссектрисе до мо­мента встречи последней точки (e_i1, e_i2). На рисунке 6 приведен пример для критерия Z_MM.

 

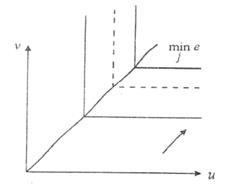
Рис. 4.8. Семейство линий уровня

 

Для критерия Гермейера вве­дение вероятностей меняет лишь угол наклона направляющей. Для критерия Сэвиджа происходит сме­щение на расстояние полезности и т.д.

Оценка принимаемого решения

Учитывая, что решения необходимо принимать в любых случаях, независимо от вида воздействий и законов распределения, приходится вводить не только доверительные интервалы для параметров, но и их коэффициенты значимости, прибегая к понятию релевантности (упорядо­чению параметров по степени их влияния). Мерой неопределённости появле­ния значения параметра принимается Шенноновская мера энтропии. При выборе одной из альтернатив в принципе возможны четыре исхода:

- принято верное в данной ситуации решение;

- отвергнуто неверное в данной ситуации решение;

- отвергнуто верное в данной ситуации решение (ошибка 1-го рода);

- принято неверное в данной ситуации решение (ошибка 2-го рода).

Первые две ситуации очевидны и не требуют пояснений. Две следую­щих ситуации широко применяются в теории математической статистики, поэтому дадим только краткий комментарий. При проверке статистических гипотез возможны две ситуации: гипотеза верна или гипотеза ошибочна и два возможных действия: отвергнуть или принять одну из гипотез. Сведём результат в таблицу 4.6.

Таблица 4.6

Ситуация	H 0 верна	H 0 неверна (H A)
Действие
Отвергнуть	α	1-b
Принять	1- α	b

Вероятности ошибочных решений в разных случаях их применения носят порой разные наименования не меняя при этом своего статистичес­кого смысла. Так:

- ошибка 1-го рода, риск 1, риск поставщика (изготовителя), риск излишней наладки технологического процесса – α – определяется вероятностью неправильного отклонения нулевой гипотезы и берется обычно в интервале от 0,01 до 0,1.

- ошибка 2-го рода, риск 2, риск заказчика (потребителя), риск незамеченной разладки технологического процесса – b – определяется вероятнос­тью принятия альтернативной гипотезы и берётся обычно от 0,1 и выше. Любое принимаемое решение характеризуется заранее задаваемой вероятнос­тью ошибки первого рода и в процессе принятия решения может возникнуть три принципиально различных случая:

1. Эмпирический доверительный фактор - известна выборка значений параметров и оценивается относительная величина отклонения теоретичес­кого среднего от минимального значения критерия.

2. Прогностический доверительный фактор - известны теоретичес­кие вероятности значений параметров. Оценивается относительная вели­чина отклонения среднего выборочного значения по серии W экспериментов от минимального значения критерия.

3. Эмпирико-прогностический доверительный фактор - относитель­ная величина отклонения среднего значения параметра от минимального оценивается для предстоящей серии W экспериментов по результатам вы­борки V проведенных.

Понятие риска

Принятие решений в условиях неопределённости связано с понятием риска. Риск отражает степень неуверенности ЛПР в правильности принимаемого решения и в возможных последствиях его реализации. Отметим, что чаще этому риску подвергаются люди, не имевшие никакого отношения к процессу принятия решения. Риск можно оценить количественно:

R = A × q, (4.34)

где А - событие, a q - вероятность его появления. При этом необходимо учитывать:

- тип угрозы (материальный или жизненно важный);

- ущерб (количественный, качественный, здоровью и т.д.);

- параметр (значение, превышение предела, вероятность).

При оценке риска необходимо строить дерево ошибок аналогичное дереву решений. Естественно, что оценки риска весьма расплывчаты. Риск субъективно привлекательной деятельности обычно занижается (альпинизм, парашютный спорт), риск событий, на которые трудно по­влиять завышается. При принятии решений необходимо выбрать раци­ональные варианты и соотнести их с ущербом или угрозой. По разным отраслям и событиям накоплена статистика, которая кладётся в основу расчётов c использованием правил Булевой алгебры. Обозначив через К_ij – сочетание неблагоприятных событий, а через N_i, – отсутствие неблагоприятных событий для рискованного варианта решения, получим полную группу событий:

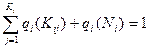, (4.35)

а риск при этом равен

, (4.36)

т.е. риск равен ожидаемой величине ущерба при принятии E_i. Сами оценки зависят от многих факторов и могут быть определены с помощью экспертных методов.

Неформальные механизмы принятия решения

При учёте риска часто используются интуитивные, а порой и эмоцио­нальные механизмы принятия решений, основывающиеся на дедуктивных, индукционных или редукционных методах или использующие методы ас­социаций, аналогий, правдоподобных рассуждений и т.п. Применение ИТ в этом случае будет вряд ли оправданно полностью. Существует однако направление, которое занимает промежуточное положение между строгими математическими методами и неформальными методами. Этим направлени­ем являются экспертные оценки, развитие вычислительной техники позво­лило создавать автоматизированные экспертные системы. Процедура экспертного оценивания достаточно хорошо разработана. Поэтому вопросы

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: