 |
Оценка параметров и характера распределения статистической совокупности
|
|
|
|
Выявление основных свойств и закономерностей исследуемой статистической совокупности необходимо начинать с построения ряда распределения единиц по одному из характеризующих их признаков. Оценка параметров ряда распределения позволит сделать вывод о степени однородности статистической совокупности, о возможности использования ее единиц для проведения научно обоснованного экономического исследования.
Рассмотрим порядок построения ряда распределения 23 хозяйств области по урожайности зерновых.
Так как данный признак изменяется непрерывно, строится вариационный ряд распределения.
1.Составим ранжированный ряд распределения предприятий по урожайности, т.е. расположим их в порядке возрастания по данному признаку (ц/га):6,3 7,7 11,6 12,4 13,3 13,7 14,8 15,1 15,2 16,6 18,8 18,8 19,6 20,1
20,5 20,8 21,0 22,0 22,1 25,8 26,0 28,6
2. Определим количество интервалов (групп)
k = 5
3. Определим шаг интервала:
где xmax и xmin - наименьшее и наибольшее значение группировочного признака
k – количество интервалов.
≈ 4,5 (руб.)
4. Определяем границы интервалов.
Для этого xmin = 6,3 принимаем за нижнюю границу первого интервала, а его верхняя граница равна: xmin+ h = 6,3 + 4,5 = 10,8. Верхняя граница первого интервала одновременно является нижней границей второго интервала. Прибавляя к ней величину интервала (h), определяем верхнюю границу второго интервала: 10,8 +4,5= 15,3
Аналогично определяем границы остальных интервалов.
5. Подсчитаем число единиц в каждом интервале и запишем в виде таблицы.
Таблица 8 – Интервальный ряд распределения хозяйств по урожайности
зерновых
| Группы хозяйств по урожайности зерновых, ц/га | Число хозяйств |
| 6,3 – 10,8 | 2 |
| 10,8 – 15,3 | 7 |
| 15,3 -19,8 | 4 |
| 19,8 – 24,3 | 6 |
| 24,3 – 28,8 | 3 |
| Итого | 22 |
|
|
|
Для наглядности интервальный ряд распределения изобразим графически в виде гистограммы.
Для выявления характерных черт, свойственных ряду распределения единиц могут быть использованы следующие показатели.
1) Для характеристики центральной тенденции распределения определяют среднюю арифметическую, моду и медиану признака.
Средняя величина признака определяется по формуле средней арифметической взвешенной:
,
где xi - варианты,
– средняя величина признака;
fi – частоты распределения.
В интервальных рядах в качестве вариантов (xi) используют серединные значения интервалов.
= 
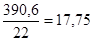ц/га
Мода – наиболее часто встречающееся значение признака, может быть определена по формуле
,
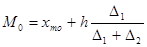где xmo – нижняя граница модального интервала;
h – величина интервала;
Δ1 – разность между частотой модального и домодального интервала;
Δ2 – разность между частотой модального и послемодального интервала.
В данной работе нужно определять две моды:
,
Медиана – значение признака, находящегося в центре ранжированного ряда распределения, определяется по формуле:
где xme – нижняя граница медиального интервала;
h – величина интервала;
Σfi – сумма частот распределения;
Sme-1 – сумма частот домедиальных интервалов;
fme – частота медиального интервала
2) Для характеристики меры рассеяния признака определяют показатели вариации: размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации составит: R = xmax – xmin = 28,6 – 6,3 = 25,5 (ц/га)
Дисперсия определяется по формуле
Среднее квадратическое отклонение признака в ряду распределения составит:
(ц/га).
Для определения коэффициента вариации используем формулу
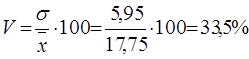
3) Для характеристики формы распределения могут быть использованы коэффициенты асимметрии (Аs) и эксцесса (Еs):
|
|
|
Т.к.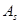 
>0, распределение имеет правостороннюю асимметрию, о которой также можно судить на основе следующего неравенства: 
< 
< 
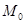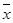
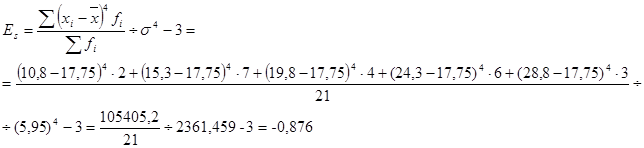Т.к. Es<0, распределение является низковершинным по сравнению с нормальным.
Для того чтобы определить подчиняется ли эмпирическое (исходное) распределение закону нормального распределения, необходимо проверить статистическую гипотезу о существенности различия частот фактического и теоретического (нормального) распределения.
Наиболее часто для проверки таких гипотез используют критерий Пирсона (χ2), фактическое значение которого определяют по формуле
где fi и fm – частоты фактического и теоретического распределения.
Теоретические частоты для каждого интервала определим в следующей последовательности:
1) Для каждого интервала определим нормированное отклонение (t):
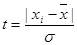
Например, для первого интервала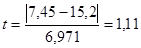 
и т.д.
Результаты расчета значений t представим в таблице 9.
2) Используя математическую таблицу “Значения функции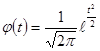 
”, при фактической величине t для каждого интервала найдем значение функции нормального распределения (таблица 9).
3) Определим теоретические частоты по формуле fm=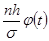 
,
где n – число единиц в совокупности;
h – величина интервала.
n = 21, h = 5,1, σ = 6,971
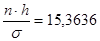
Таблица 9 – Эмпирическое и теоретическое распределение предприятий по
урожайности зерновых
| Срединное значение интервала по урожайности,ц | Число хозяйств | 
| 
|
| 
|
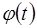
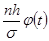
| fi | t | табличное | fm | - |
| 7,45 | 6 | 1,11 | 0,2155 | 4 | 1,00 |
| 12,55 | 6 | 0,38 | 0,3712 | 6 | 0,00 |
| 14,65 | 4 | 0,35 | 0,3752 | 6 | 0,67 |
| 22,75 | 2 | 1,08 | 0,2227 | 4 | 1,00 |
| 27,85 | 3 | 1,81 | 0,0775 | 1 | 4,00 |
| Итого | 21 | x | x | 21 | 6,67 |
4) Подсчитаем сумму теоретических частот и проверим ее равенство фактическому числу единиц, т.е.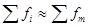 
.(21=21)
Таким образом, фактическое значение критерия составило 
=6,67.
По математической таблице “Распределение χ2” определяем критическое значение критерия χ2 при числе степеней свободы (ν) равном числу интервалов минус единица и выбранном уровне значимости (в экономических исследованиях чаще всего используют уровень значимости равный 0,05). При ν = 5 – 1 = 4 и α=0,05 
=9,95
Поскольку фактическое значение критерия (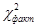
) меньше табличного (), отклонение фактического распределения от теоретического следует признать несущественным.
|
|
|
Таким образом, средняя урожайность зерновых составила 15,2 ц с 1 га при среднем квадратичном отклонении 6,97 ц/га.
Так как коэффициент вариации больше 33%, совокупность единиц является неоднородной: V=45,9%.
Эмпирическое распределение имеет правостороннюю асимметрию, т.к. 
< 
< 
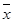и 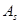>0 и является низковершинным по сравнению с нормальным распределением, т.к. 
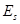<0. При этом отклонение фактического распределения от нормального является несущественным. Следовательно, исходную совокупность единиц можно использовать для проведения экономико-статистического исследования при условии исключения из нее нетипичных предприятий.
|
|
|
