 |
Автокорреляция уровней временного ряда
|
|
|
|
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции имеет вид:
(4.1)
где
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда 
и 
.
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями 
и 
и определяется по формуле:
(4.2)
где
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше 
.
Свойства коэффициента автокорреляции.
1. Он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
|
|
|
2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка 
, то ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.
Рассмотрим пример. Пусть имеются некоторые условные данные об общем количестве правонарушений на таможне одного из субъектов РФ (например, Республики Татарстан).
|
|
|
Таблица 4.1
| Год | Квартал |
| Количество возбужденных дел,
|
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV |
Построим поле корреляции:
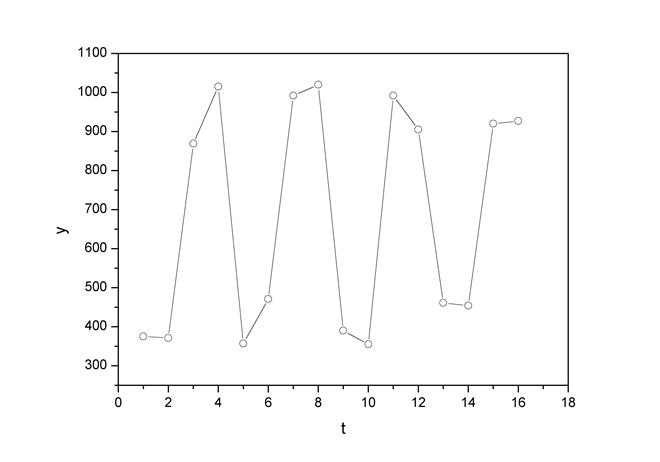
Рис. 4.4.
Уже исходя из графика видно, что значения 
образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу.
Таблица 4.2
| 
| 
| 
| 
| 
| 
| 
|
| – | – | – | – | – | – | ||
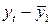
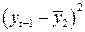
| -328,33 | -288,13 | 94601,72 | 107800,59 | 83018,90 | |||
| 169,67 | -292,13 | -49565,70 | 28787,91 | 85339,94 | |||
| 315,67 | 205,87 | 64986,98 | 99647,55 | 42382,46 | |||
| -342,33 | 351,87 | -120455,66 | 117189,83 | 123812,50 | |||
| -228,33 | -306,13 | 69898,66 | 52134,59 | 93715,58 | |||
| 292,67 | -192,13 | -56230,69 | 85655,73 | 36913,94 | |||
| 320,67 | 328,87 | 105458,74 | 102829,25 | 108155,48 | |||
| -309,33 | 356,87 | -110390,60 | 95685,05 | 127356,20 | |||
| -344,33 | -273,13 | 94046,85 | 118563,15 | 74600,00 | |||
| 292,67 | -308,13 | -90180,41 | 85655,73 | 94944,10 | |||
| 205,67 | 328,87 | 67638,69 | 42300,15 | 108155,48 | |||
| -238,33 | 241,87 | -57644,88 | 56801,19 | 58501,10 | |||
| -245,33 | -202,13 | 49588,55 | 60186,81 | 40856,54 | |||
| 220,67 | -209,13 | -46148,72 | 48695,25 | 43735,36 | |||
| 227,67 | 256,87 | 58481,59 | 51833,63 | 65982,20 | |||
| Сумма | 9,05 | 0,05 | 74085,16 | 1153766,39 | 1187469,73 | ||
| Среднее значение | 699,33 | 663,13 | – | – | – | – | – |
Следует заметить, что среднее значение получается путем деления не на 16, а на 15, т.к. у нас теперь на одно наблюдение меньше.
Теперь вычисляем коэффициент автокорреляции первого порядка по формуле (4.1):
.
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка.
Таблица 4.3
|
|
| 
| 
| 
| 
| 
| 
|
| – | – | – | – | – | – | ||
| – | – | – | – | – | – | ||
| 145,57 | -269,79 | -39273,33 | 21190,62 | 72786,64 | |||
| 291,57 | -273,79 | -79828,95 | 85013,06 | 74960,96 | |||
| -366,43 | 224,21 | -82157,27 | 134270,94 | 50270,12 | |||
| -252,43 | 370,21 | -93452,11 | 63720,90 | 137055,44 | |||
| 268,57 | -287,79 | -77291,76 | 72129,84 | 82823,08 | |||
| 296,57 | -173,79 | -51540,90 | 87953,76 | 30202,96 | |||
| -333,43 | 347,21 | -115770,23 | 111175,56 | 120554,78 | |||
| -368,43 | 375,21 | -138238,62 | 135740,66 | 140782,54 | |||
| 268,57 | -254,79 | -68428,95 | 72129,84 | 64917,94 | |||
| 181,57 | -289,79 | -52617,17 | 32967,66 | 83978,24 | |||
| -262,43 | 347,21 | -91118,32 | 68869,50 | 120554,78 | |||
| -269,43 | 260,21 | -70108,38 | 72592,52 | 67709,24 | |||
| 196,57 | -183,79 | -36127,60 | 38639,76 | 33778,76 | |||
| 203,57 | -190,79 | -38839,12 | 41440,74 | 36400,82 | |||
| Сумма | -0,02 | -0,06 | -1034792,71 | 1037835,43 | 1116776,36 | ||
| Среднее значение | 723,43 | 644,79 | – | – | – | – | – |
Следовательно
|
|
|
.
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу.
Таблица 4.4
| Лаг | Коэффициент автокорреляции уровней |
| 0,063294 | |
| –0,961183 | |
| –0,036290 | |
| 0,964735 | |
| 0,050594 | |
| –0,976516 | |
| –0,069444 | |
| 0,964629 | |
| 0,162064 | |
| -0,972918 | |
| -0,065323 | |
| 0,985761 |
Коррелограмма:
Рис. 4.5.
Анализ коррелограммы и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
|
|
|
