 |
Элементарные преобразования матриц
|
|
|
|
Определение матрицы. Виды матриц.
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i - номер строки матрицы, а j - номер столбца матрицы. У матрицы есть 2 диагонали. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ матрицы, а элементы стоящие на другой диагонали образуют вспомогательную диагональ матрицы.
Матрица записывается ввиде:

Матрицу А называют матрицей размера "m×n" и пишут Аm×n. Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.
А = В, если aij = bij. Матрица А называется симметричной, если она квадратная и если все aij= аji.
Если (m = n), то матрица называется квадратной. Квадратную матрицу размера "n×n" называют матрицей n - ого порядка. Квадратную матрицу, у которой все элементы, кроме элементов главной диагонали, равны нулю, называю диагональной матрицей. Диагональная матрица:

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной матрицей. Обозначается буквой Е. Единичная матрица:
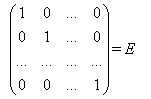
Квадратная матрица, называется треугольной, если все элементы матрицы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается буквой О. В матричном исчисленииматрицы О и Е играют роль 0 и 1 в арифметике. Матрица, содержащая одну строку или один столбец, называется вектором (Или вектор-строка, или вектор-столбец соответственно).
|
|
|
Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированиемматрицы, если элементы каждой строки матрицы А записать в том же порядке в столбцыматрицы В. Обозначается АТ.
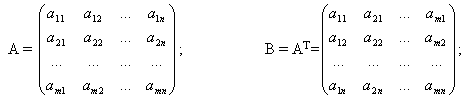
Другими словами, aij = bji.
Операции над матрицами: сложение, умножение матрицы на число, умножение матриц.
Вычитание и сложение матриц сводится к соответствующим операциям над их элементами.Операция сложения матриц вводится только для матриц одинакового размера, т. е. дляматриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов.
С = А + В
cij = aij + bij
Аналогично определяется разность матриц.
Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что bij = k × aij.
В = k × A
bij = k × aij.
Матрица - А = (-1) × А называется противоположной матрице А.
Свойства сложения матриц и умножения матрицы на число:
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А;
2. А + (В + С) = (А + В) + С;
3. А + 0 = А;
4. А - А = 0;
5. 1 × А = А;
6. α × (А + В) = αА + αВ;
7. (α + β) × А = αА + βА;
8. α × (βА) = (αβ) × А;
, где А, В и С - матрицы, α и β - числа.
Элементарные преобразования матриц
Элементарными преобразованиями матрицы называются следующие преобразования:
1) умножение строки матрицы на число, отличное от нуля;
2) прибавление к одной строке матрицы другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование матрицы;
|
|
|
Те же операции, применяемые для столбцов матрицы, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу матрицы прибавить линейную комбинацию остальных строк (столбцов).
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первойматрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что
сik = ai1 × b1k + ai2 × b2k +... + ain × bnk,
т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.
Свойства матриц:
Умножение матриц обладает следующими свойствами:
1. А × (В × С) = (А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В) × С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0 = 0; 0 × А = 0;
6. (АВ)Т = ВТАТ;
7. (АВС)Т = СТВТАТ;
8. (А + В)Т = АТ + ВТ
|
|
|


