 |
Вектор на прямой, на плоскости, в пространстве
|
|
|
|
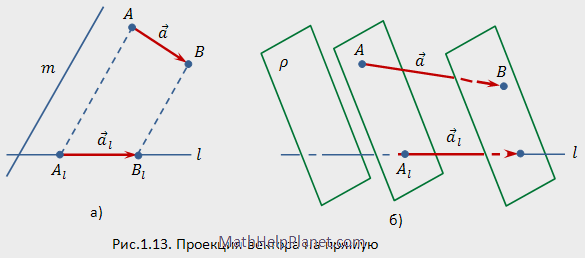
Пусть в пространстве дана прямая  и пересекающая ее плоскость
и пересекающая ее плоскость 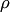 . Проекцией вектора
. Проекцией вектора 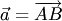 на прямую
на прямую  параллельно плоскости
параллельно плоскости 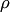 (вдоль плоскости
(вдоль плоскости 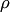 ) называется вектор
) называется вектор  , началом которого служит проекция
, началом которого служит проекция 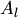 , начала
, начала 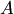 , а концом — проекция
, а концом — проекция 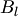 конца
конца 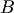 вектора
вектора 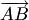 (рис. 1.13,6). Если плоскость
(рис. 1.13,6). Если плоскость 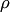 перпендикулярна прямой
перпендикулярна прямой  , то проекция называется ортогональной.
, то проекция называется ортогональной.
Проекция вектора на плоскость
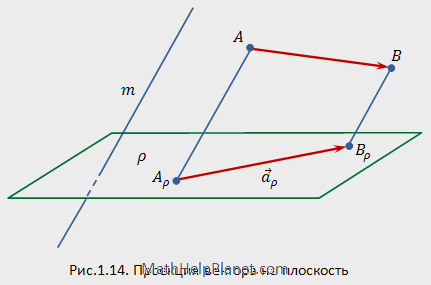
Пусть в пространстве задана плоскость я и пересекающая ее прямая 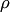 . Проекцией вектора
. Проекцией вектора 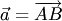 на плоскость
на плоскость 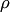 параллельно прямой
параллельно прямой 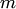 (вдоль прямой
(вдоль прямой 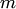 ) называется вектор
) называется вектор 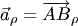 , началом которого служит проекция
, началом которого служит проекция  начала
начала 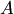 , а концом — проекция
, а концом — проекция  конца
конца 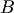 вектора
вектора 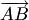 (рис. 1.14). Если прямая
(рис. 1.14). Если прямая 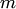 перпендикулярна плоскости
перпендикулярна плоскости 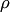 , то проекция называется ортогональной.
, то проекция называется ортогональной.
Свойства проекций векторов
1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.
2. Проекции равных векторов равны.
3. Проекция суммы векторов равна сумме их проекций.
4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).
5. Проекция линейной комбинации векторов равна линейной комбинации проекций
Введению в теорию линейных пространств
В дальнейшем через R обозначается поле вещественных чисел, через N — множество целых, а через N + — множество натуральных чисел. Вещественное векторное пространство (или, вещественное линейное пространство) представляет собой множество E элементов произвольной природы (его точки называются векторами), в котором определены операции сложения векторов +: E × E → E и умножения на число ·: R × E → E, удовлетворяющие следующим аксиомам: при всех x, y, z ∈ E и α, β ∈ R
|
|
|
Линейная зависимость. Геометрический смылс
некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или
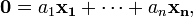
где не все числа 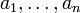 равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.
Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:
§ если строки матрицы C линейно зависят от строк матрицы B, то C = AB для некоторой матрицы A;
§ если столбцы матрицы C линейно зависят от столбцов другой матрицы A, то C = AB для некоторой матрицы B.
Ранг матрицы
Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.
Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.
Базисом 1) ненулевого векторного пространства 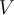 над полем
над полем 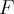 называется система векторов, которая
называется система векторов, которая
1. порождает 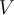 ,
,
2. линейно независима.
Теорема 1. Ненулевое векторное пространство 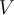 всегда обладает базисом. Иными словами,
всегда обладает базисом. Иными словами, 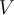 являетсясвободным
являетсясвободным 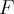 -модулем.
-модулем.
Определение 2. Размерностью 2) ненулевого векторного пространства 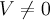 называется мощность его базиса. Для нулевого векторного пространства
называется мощность его базиса. Для нулевого векторного пространства 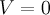 полагают, что его размерность равна нулю. Размерностьвекторного пространства
полагают, что его размерность равна нулю. Размерностьвекторного пространства 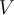 над полем
над полем 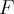 обозначается через
обозначается через 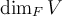
|
|
|
|
|
|


