 |
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.
|
|
|
|
Миноры и алгебраические дополнения. Теорема Лапласа.
Миноры матрицы
Пусть дана квадратная матрица А, n - ого порядка. Минором некоторого элемента аij,определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.
Рассмотрим на примере определителя матрицы 3 - его порядка:
, тогда согласно определению минора, минором М12, соответствующим элементу а12, будетопределитель:
При этом, с помощью миноров можно облегчать задачу вычисления определителя матрицы. Надо разложить определитель матрицы по некоторой строке и тогда определитель будет равен сумме всех элементов этой строки на их миноры. Разложение определителя матрицы 3 - его порядка будет выглядеть так:
|
| 
|
, знак перед произведением равен (-1)n, где n = i + j.
Алгебраические дополнения:
Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij.
Аij = (-1)i+j × Мij.
Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведение элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения. Пример:
Теорема ЛАПЛАСА
Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(*)
(разложение по элементам i-й строки);
(**)
(разложение по элементам j-го столбца).
Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки
|
|
|
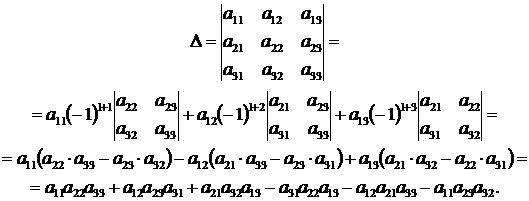
Что совпадает с определением определителя матрицы третьего порядка.
Разложение определителя по строке или столбцу. Определитель квазитреугольной матрицы.
Разложение определителя
По элементам i-й строки:
По элементам j-го столбца:
Например, при n = 4 разложение по первой строке
Квазитреугольная матрица
Квазитреугольной называется клеточная матрица A у которой клетки Aij = 0 при i > j (или i < j):
.
Определитель квазитреугольной матрицы равен произведению определителей диагональных клеток.
Обратная матрица
Если существуют квадратные матрицы Х и А, удовлетворяющие условию:
X × A = A × X = E
, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной матрицей к матрице А и обозначается А-1. Всякая невырожденная матрица имеет обратную матрицу и притом только одну, т. е. для того чтобы квадратная матрица A имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля.
Для получения обратной матрицы используют формулу:
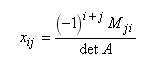
, где Мji дополнительный минор элемента аji матрицы А.
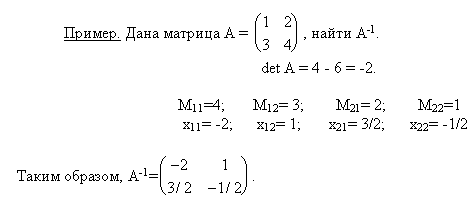
Cвойства обратных матриц:
1) (А-1)-1 = А;
2) (АВ)-1 = В-1А-1;
3) (АТ)-1 = (А-1)Т;
Множество
Множество - это совокупность объектов, рассматриваемая как одно целое. Основное отношение между элементом a и содержащим его множеством A обозначается так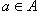 
(a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут 
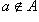(a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так { a, b, c } обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3,...}, а множество четных чисел {2, 4, 6,...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.
|
|
|
Эквивалентность.
Отношение эквивалентности (∼) на множестве X — это бинарное отношение, для которого выполнены следующие условия:
1. Рефлексивность: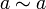 
для любого a в X,
2. Симметричность: если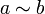 
, то 
,
3. Транзитивность: если 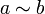и 
, то 
.
Запись вида «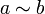» читается как «a эквивалентно b».
Геометрические векторы
Вектором в пространстве называется направленный отрезок, то есть такой отрезок, один из концов которого выделен и называется началом, а другой — концом. При этом сонаправленные и равные по длине отрезки считаются одним и тем же вектором
Направленным отрезком называется упорядоченная пара (A,B) точек пространства, у которой A называется началом, B — концом. Направленные отрезки (A,B) и (C,D) назовём эквивалентными, если 
или если 
и 
. Знак 
обозначает сонаправленность: если луч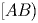и 
и 
либо лежат на одной прямой и дают в пересечении луч, либо лежат на параллельных прямых в одной полуплоскости относительно прямой 
. Классы эквивалентности по указанному отношению называются векторами.
Свободный вектор.
Два вектора называются равными, если они:
а) коллинеарны, одинаково направлены;
б) имеют равные длины.
Все нулевые векторы считаются равными друг другу.
Это определение равенства векторов характеризует так называемые свободные векторы. Данный свободный вектор можно переносить, не меняя его направления и длины, в любую точку пространства (откладывать от любой точки), при этом будем получать векторы, равные данному. Таким образом, свободный вектор определяет целый класс равных ему векторов, отличающихся только точкой приложения.
|
|
|
