Методические указания по выполнению расчетно-графической работы

В общем виде теоретическую линейную парную регрессионную модель можно представить в виде:

Y = или y_i = , i=1,2,…,n;

где Y – объясняемая (результирующая, зависимая, эндогенная) переменная,

Х – объясняющая (факторная, независимая, экзогенная) переменная или регрессор;

- теоретические параметры (числовые коэффициенты) регрессии, подлежащие оцениванию;

ε_i - случайное отклонение (возмущение, ошибка).

Основные гипотезы:

1. y_i = , i=1,2,…,n, - спецификация модели.

2. Х – детерминированная (неслучайная) величина, при этом предполагается, что среди значений x_i – не все одинаковые.

3а. М ε_i =0, i=1,2,…,n.

3b. D ε_i =σ², i=1,2,…,n. Условие независимости дисперсии ошибки от номера наблюдения называется гомоскедастичностью; случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью.

3с. М(ε_i ε_j)=0 при i ≠ j, некоррелированность ошибок для разных наблюдений. В случае, когда это условие не выполняется, говорят об автокорреляции ошибок.

1. Возмущения являются нормально распределенными случайными величинами: ε_i ≈ N(0, σ²).

Замечание. Для получения уравнения регрессии достаточно первых трех предпосылок. Для оценки точности уравнения регрессии и его параметров необходимо выполнение четвертой предпосылки.

Задача линейного регрессионного анализа состоит в том, чтобы по имеющимся статистическим данным (x_i, y_i), i=1,2,…,n, для переменных X и Y получить наилучшие оценки неизвестных параметров , т. е. построить так называемое эмпирическое уравнение регрессии

,

где оценка условного математического ожидания М(Y/ X=x_i); оценки неизвестных параметров , называемые эмпирическими коэффициентами регрессии. В каждом конкретном случае можно записать

, i=1,2,…,n,

где отклонения е_i – ошибки (остатки) модели, которые являются оценками теоретического случайного отклонения ε_i.

2. Рассчитайте параметры выборочного уравнения линейной регрессии с помощью метода наименьших квадратов (МНК)

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). В методе наименьших квадратов оценки параметров модели строятся так, чтобы минимизировать сумму квадратов ошибок модели по всем наблюдениям. Таким образом, критерий наименьших квадратов записывается в виде:

Необходимым условием существования минимума функции S(b₀ ,b₁) является равенство нулю её частных производных по неизвестным b₀ и b₁ (для краткости опустим индексы суммирования у знака суммы Σ):

Данная система уравнений называется системой нормальных уравнений для коэффициентов регрессии.

Решая эту систему двух линейных уравнений с двумя неизвестными, например, методом подстановки, получим:

где выборочные средние значения переменных Х и Y.

.

С геометрической точки зрения минимизация суммы квадратов отклонений означает выбор единственной прямой (из всех прямых с параметрами), которая ближе всего «прилегает» по ординатам к системе выборочных точек (x_i, y_i), i=1,2,…,n.

3. Оцените тесноту связи с помощью показателей корреляции (выборочный коэффициент корреляции) и детерминации

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_xy. Существует несколько видов формулы линейного коэффициента корреляции, основные из них:

.

Корреляционная связь между переменными называется прямой, если r_xy.>0, и обратной, если r_xy <0.

Для практических расчётов наиболее удобна формула

,

так как по ней коэффициент корреляции находится из данных наблюдений, и на значение r_xy не оказывает влияния погрешность округления.

Коэффициент корреляции принимает значения от -1 до +1.

При значении коэффициента корреляции равном 1 связь представлена линейной функциональной зависимостью. При этом все наблюдаемые значения располагаются на линии регрессии.

При r_xy =0 корреляционная связь между признаками в линейной форме отсутствует. При этом линия регрессии параллельна оси Ох.

При r_xy > 0 – корреляционная связь между переменными называется прямой, а при r_xy < 0 – обратной.

Для характеристики силы связи можно использовать шкалу Чеддока.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r_xy², называемый коэффициентом детерминации. Коэффициент детерминации обозначим R², т. о. имеем

R² = r_xy².

Коэффициент детерминации характеризует долю дисперсии результативного признака Y, объясняемую регрессией, в общей дисперсии результативного признака. Соответственно величина 1- R² характеризует долю дисперсии Y, вызванную влиянием остальных, не учтенных в модели факторов.

Замечание. Вычисление R² корректно, если константа включена в уравнение регрессии.

4. Используя критерий Стьюдента оцените статистическую значимость коэффициентов регрессии и корреляции

Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Очевидно, что коэффициенты эмпирического уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. При проведении статистического анализа возникает необходимость сравнения эмпирических коэффициентов регрессии b₀ и b₁ с некоторыми теоретически ожидаемыми значениями этих коэффициентов. Данный анализ осуществляется по схеме статистической проверки гипотез.

Для проверки гипотезы

Н ₀ : b₁ = β₁,

Н ₁: b₁ ≠ β₁

используется статистика , которая при справедливости гипотезы Н₀ имеет распределение Стьюдента с числом степеней свободы df = n – 2, где - стандартная ошибка коэффициента регрессии b₁, .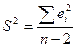

Наиболее важной на начальном этапе статистического анализа построенной модели является задача установления наличия линейной зависимости между Y и X. Эта проблема может быть решена проверкой гипотезы

Н ₀ : b₁ = 0,

Н ₁: b₁ ≠ 0.

Гипотеза в такой постановке обычно называется гипотезой о статистической значимости коэффициента регрессии. При этом если принимается нулевая гипотеза, то есть основания считать, что величина Y не зависит от Х – коэффициент b₁ статистически незначим (он слишком близок к нулю). При отклонении Н ₀ коэффициент считается статистически значимым, что указывает на наличие определённой линейной зависимости между Y и X. Используемая в этом случае t – статистика имеет вид: и при нулевой гипотезе имеет распределение Стьюдента с (n -2) степенями свободы.

Если вычисленное значение t – статистики - |t факт| при заданном уровне значимости α больше критического (табличного) t табл, т.е.

|t факт| > t табл = t(α; n-2),

то гипотеза Н ₀ : b₁ = 0, отвергается в пользу альтернативной при выбранном уровне значимости. Это подтверждает статистическую значимость коэффициента регрессии b₁.

Если |t факт| < t табл = t(α; n-2), то гипотеза Н₀ не отвергается. Критическое значение t табл = t(α;n-2), при заданном уровне значимости α и числе степеней свободы n -2 находится по таблицам 2 Приложения.

По аналогичной схеме на основе t – статистики проверяется гипотеза о статистической значимости коэффициента b₀:

,

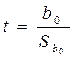где и - стандартная ошибка коэффициента регрессии b₀ .

1. Постройте интервальные оценки параметров регрессии. Проверьте, согласуются ли полученные результаты с выводами, полученными в предыдущем пункте

Формулы для расчета доверительных интервалов имеют следующий вид:

,

,

которые с надёжностью (1 – α) накрывают определяемые параметры .

Если в границы доверительных интервалов попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр признается статистически незначимым.

6. Постройте таблицу дисперсионного анализа для оценки значимости уравнения в целом

Проверить значимость уравнения регрессии – значит, установить, соответствует ли математическая модель, выражающая зависимость между переменными, имеющимся данным и достаточно ли включённых в уравнение объясняющих переменных для описания зависимой переменной.

Оценка значимости уравнения в целом дается с помощью F – критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. H₀ : β₁=0, следовательно, фактор не оказывает влияния на результат.

Непосредственному расчету F – критерия предшествует анализ дисперсии результативного признака Y. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – «объясненную» и «остаточную» («необъясненную»):

= +

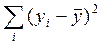Общая сумма квадратов Сумма квадратов Остаточная сумма

отклонений = отклонений, объясненная + квадратов

регрессией отклонений

Обозначим SS_общ = , SS_R = и SS_ост = .

Любая сумма квадратов отклонений связана с числом степеней свободы df (degree of freedom), т.е. с числом свободы независимого варьирования признака.

Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Число степеней свободы остаточной суммы квадратов при линейной парной регрессии составляет n - 2, общей суммы квадратов – n -1 и число степеней свободы для факторной суммы квадратов, т. е. объясненной регрессией равно единице. Имеем равенство:

n – 1 = 1+ (n – 2).

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы.

;

;

.

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F –отношения или F – критерий, статистика которого F при нулевой гипотезе

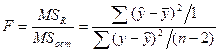~ F(1,n-2)

распределена по закону Фишера со степенями свободы (1, n-2).

Если вычисленное значение F –отношения - F факт при заданном уровне значимости α больше критического (табличного) F табл, т.е.

F факт > F табл = F(α;1,n-2),

то гипотеза Н₀ : β₁=0 отвергается, признаётся статистическая значимость уравнения регрессии, т.е. связь между рассматриваемыми признаками есть и результаты наблюдений не противоречат предположению о её линейности.

Если F факт < F табл = F(α;1,n-2), то гипотеза Н₀ не отвергается, уравнение регрессии считается статистически незначимым.

Критическое значение F табл = F(α;1,n-2), при заданном уровне значимости α и числе степеней свободы 1; n -2 находится по таблицам Приложения 4.

Величина F – критерия связана с коэффициентом детерминации R². Значение F – критерия можно выразить следующим образом:

.

Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа.

Дисперсионный анализ результатов регрессии

Источники вариации	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы	F - отношение
фактиче- ское	таблич- ное
Объясненная	1
Остаточная	n– 2			F табл = F(α;1,n-2)
Общая	n– 1

Для расчёта коэффициента детерминации можно использовать формулу:

.

Максимальное значение коэффициента R² равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что для всех i и все остатки равны нулю.

Если в выборке отсутствует видимая связь между X и Y, то коэффициент детерминации будет близок к нулю.

Легко показать, что принцип минимизации суммы квадратов остатков при выполнении определённых условий эквивалентен минимизации дисперсии остатков, следовательно, автоматически максимизируется коэффициент детерминации.

7. С помощью теста Гольдфельда – Квандта исследуйте гетероскедастичность остатков. Сделайте выводы

Гетероскедастичность остатков – это свойство остатков, которое заключается в том, что их дисперсии или разбросы для каждого фиксированного Х являются неоднородными или неодинаковыми.

Для обнаружения гетероскедастичности остатков используется визуальный анализ графика зависимости Y от Х, линии тренда и остатков.

При малом объёме выборки для оценки гетероскедастичности используют тест Гольдфельда-Квандта, разработанный в 1965г. М.Г. Гольдфельд и Р.Э. Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора, остатки распределены нормально и не подвержены автокорреляции.

a. упорядочить все n наблюдений по величине Х;

b. исключить из рассмотрения «с» центральных наблюдений;

c. оценить МНК отдельные регрессии для первых n₁= и последних n₂= наблюдений;

Замечание. Мощность критерия зависит от выбора значения n₁ и n₂ по отношению к n. Обычно выбирают n₁ = n₂ таким образом, чтобы вся совокупность разделилась на три равные части. Однако М.Г. Гольдфельд и Р.Э. Квандт уточняют это правило и рекомендуют брать значения n₁ = n₂= 11, если n=30 и n₁ = n₂ =22, если n=60 [1].

Выдвигается основная гипотеза H₀ об отсутствии гетероскедастичности и формируется статистика критерия F, которая в случае справедливости нулевой гипотезы имеет распределение Фишера-Снедекора соответственно со степенями свободы числителя и знаменателя n₂ -2 и n₁ -2.

ü рассчитать значение критерия Фишера 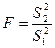, где и - дисперсии остатков регрессий для первой и последней групп наблюдений соответственно;

ü принять статистическое решение:

если F факт > F табл = F(α; n₂-2, n₁-2), то гипотеза H₀ отвергается и с вероятностью 1-α утверждается, что гетероскедастичность остатков является достоверной, в противном случае наличие гетероскедастичности является недоказанной.

8. В случае пригодности линейной модели рассчитайте прогнозное значение результата, если значение фактора увеличится на 5% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05

Построенная адекватная модель может использоваться для прогнозирования.

§ Точечный прогноз по уравнению регрессии.

Если известно значение независимой переменной х_р, то прогноз зависимой переменной осуществляется подстановкой этого значения в полученное эмпирическое уравнение регрессии .

Показателем точности прогноза служит его дисперсия (чем она меньше, тем точнее прогноз):

Подставив вместо её несмещённую оценку 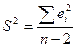, получим выборочную исправленную дисперсию рассматриваемой случайной величины.

Очевидно, что чем больше объем выборки, тем точнее прогноз. При фиксированном объёме выборки прогноз тем точнее, чем больше вариация выборочных данных и чем ближе значение независимой переменной х_р к среднему выборочному значению.

§ Интервальный прогноз среднего значения по уравнению регрессии.

Доверительный интервал для М(Y/X=x_р) имеет вид:

§ Интервальный прогноз индивидуальных значений зависимой переменной. Интервал

определяет границы, за пределами которых могут оказаться не более 100α% точек наблюдений при Х=х_р. Данный доверительный интервал шире доверительного интервала для условного математического ожидания.

9. Оцените полученные результаты, проинтерпретируйте полученное уравнение регрессии

Существуют два этапа интерпретации уравнения регрессии. Первый этап состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. На втором этапе необходимо решить, следует ли ограничиться этим или провести более детальное исследование зависимости.

Интерпретация линейного уравнения регрессии.

Можно сказать, что увеличение х на одну единицу (в единицах измерения переменной х) приведёт к увеличению значения y на b₁ единиц (в единицах измерения переменной y).

Постоянная b₀ дает прогнозируемое значение у (в единицах у), если х=0. Это может иметь или не иметь ясного смысла в зависимости от конкретной ситуации.